01. Geometry Basics - Cardiff Tutor Company

Question 1

Line $ADB$ is a straight line.

Find the angle $CDB$ shown below:

Select the correct answer from the list below:

A: $100\degree$

B: $80\degree$

C: $60\degree$

D: $45\degree$

CORRECT ANSWER: B: $80\degree$

WORKED SOLUTION:

Angles on a strightline such as $ADB$ , will add up to $180\degree$ ,

So given the angle $ADC$ is shown to be $100\degree$ ,

angle $CDB=180\degree-100\degree=80\degree$

Level 3

Question 2

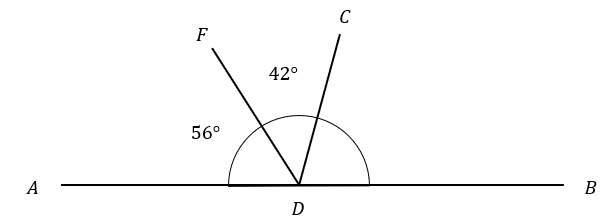
Line $ADB$ is a straight line.

Find the angle $CDB$ shown below:

Select the correct answer from the list below:

A: $48\degree$

B: $56\degree$

C: $98\degree$

D: $82\degree$

CORRECT ANSWER: D: $82\degree$

WORKED SOLUTION:

Angles on a strightline will add up to $180\degree$ ,

So given the angles shown,

angle $CDB=180\degree-56\degree-42\degree=82\degree$

Level 3

Question 3

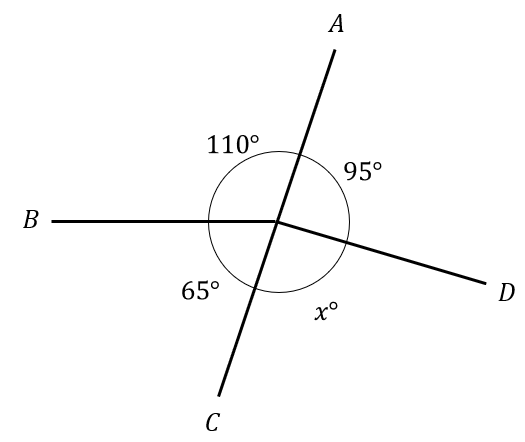
$ABCD$ are points on a circle.

Find the value of $x$

Select the correct answer from the list below:

A: $360\degree$

B: $100\degree$

C: $90\degree$

D: $180\degree$

CORRECT ANSWER: C: $90\degree$

WORKED SOLUTION:

Angles about a point will add up to $360\degree$ ,

So given the angles shown,

angle $x=360\degree-65\degree-110\degree-95\degree=90\degree$

Level 3

Question 4

$ABC$ forms an isosceles triangle shown below.

Find the value of $x$

Select the correct answer from the list below:

A: $65\degree$

B: $55\degree$

C: $50\degree$

D: $60\degree$

CORRECT ANSWER: A: $65\degree$

WORKED SOLUTION:

Angles in a triangle will add up to $180\degree$ ,

So given the angle shown and by use of the properties of an isosceles triangle,

angle $x=(180\degree-50\degree) \div 2=65\degree$

Level 3

Question 5

$ABC$ forms an isosceles triangle shown below.

Find the value of $x$

Select the correct answer from the list below:

A: $50\degree$

B: $72\degree$

C: $54\degree$

D: $58\degree$

CORRECT ANSWER: C: $54\degree$

WORKED SOLUTION:

Angles in a triangle will add up to $180\degree$ ,

So given the angle shown and by use of the properties of an isosceles triangle,

angle $x=(180\degree-72)\div2=54\degree$

Level 3

Question 6

$ABCD$ forms a quadrilateral shown below.

Find the value of $x$

Select the correct answer from the list below:

A: $85\degree$

B: $95\degree$

C: $105\degree$

D: $115\degree$

CORRECT ANSWER: D: $115\degree$

WORKED SOLUTION:

Angles in a quadrilateral will add up to $360\degree$ ,

So given the angles shown,

angle $x=360\degree-110\degree-75\degree-60\degree=115\degree$

Level 3