Q1
Q1(a)
Simplify h^2 \times h^6
Answer type: multiple choice
Answer: h^8
Wrong answers:
h^{12}
h^{64}
h^{36}
Workings:
h^2\times h^6 = h^{2+6}=h^81 mark
Q1(b)
Simplify (2x^2y^3)^4
Answer type: multiple choice
Answer: 16x^8y^{12}
Wrong Answers:
2x^8y^{12}
8x^6y^7
2x^6y^7
Workings:
(2x^2y^3)^4=2^4 \times x^{2\times4}\times y^{3\times4}=16x^8y^{12}
2 marks
1(c)
Simplify \dfrac{27a^8b^5}{3a^3b^2}
Answer type: multiple choice
Answer: 9a^5b^3
Wrong Answers:
9a^{\frac{8}{3}}b^{\frac{5}{2}}
9a^4b^3
3a^5b^4
Workings:
\dfrac{27a^8b^5}{3a^3b^2}=\dfrac{27}{3}\times\dfrac{a^8}{a^3}\times\dfrac{b^5}{b^3}=9\times a^{8-3}\times b^{5-2}=9a^5b^3
2 marks
Q2
2(a)
Find the lowest common multiple (LCM) of 18 and 28
Answer type: simple
Answer: 252
Workings:
The prime factor trees of 18 and 28 are as follows

Putting these prime numbers into a Venn diagram gives:

Multiplying the numbers in the Venn diagram together gives the LCM:
2\times2\times3\times3\times7=4\times9\times7=36\times7=2522 marks
2(b)
M=2^3\times 3\times5\times7 \quad \quad N=2^2\times3^3\times7\times11Write down the highest common factor (HCF) of M and N.
Answer type: simple
Answer: 84
Workings:
Putting the prime numbers from M and N into a Venn diagram gives:
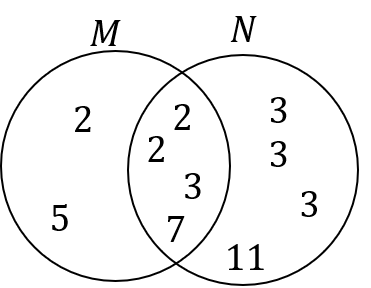
The HCF is given by the product of the numbers in the intersection:
\text{HCF } = 2\times2\times3\times7=4\times3\times7=12\times7=841 mark
3
The line R is shown on the grid.

Find an equation for line R.
Answer type: multiple choice
Answer: y=-2x+1
Wrong Answers:
y=0.5x+1
y=-2x+0.5
y=-0.5x+1
Workings:
The line has a gradient of -2 and a y-intercept of +1 so the equation is y=-2x+1
3 marks
Q4
Sana buys a new car worth £7650 and gets a discount of 25 \%
Sana pays a deposit for the car.
She then pays the rest of the cost in 24 equal monthly payments of £168.75
Find the ratio of the deposit Sana pays to the total of the 24 equal payments.
Give your answer in its simplest form.
Answer type: multiple choice
Answer: 12:5
Wrong Answers:
13:7
4:5
8:3
Workings:
The total of the monthly payments is £168.25\times24 = £4050
The amount Sana pays for the car is £7650\times0.75=£5737.50
The deposit she pays is the difference: 5737.50-4050=£1687.5
The ratio of the deposit to the monthly payments is therefore: 1687.50 : 4050
This can be simplified: \dfrac{4050}{1687.50}=\dfrac{12}{5}
Hence the ratio is 12:5
5 marks
Q5
5(a) Below is an incomplete table of values for y=x^2+x-2

Complete the table by giving the values of a, b, c , d and e
Answer type: multiple answers
Answers:
a = 4
b = 0
c = -2
d = 0
e = 10
Workings:
Substitute each value of x into the equation y=x^2+x-2,
e.g. for x=-3: y= (-3)^2+(-3)-2 = 9-3-2=4
2 marks
5(b)
Which of the following graphs corresponds to the graph of y=x^2+x-2 for values of x from -3 to 3?
Answer type: multiple choice
Answer:

Wrong Answers:



Workings:
Plotting the points from table on the correct axis will give the correct graph.
2 marks
5(c)
Using your answer from part (b), find estimates of the solutions to the equation x^2+x-2=2
Answer type: multiple choice
Answer: x=-2.6 and x=1.6
Wrong Answers:
x=-1.6 and x=2.6
x=-3 and x=2
x=-2 and x=3
Workings:
The solutions to x^2-x-2=2 are the values of x at y=2
Reading from the correct graph from part (b), these are approximately x=-2.6 and x=1.6
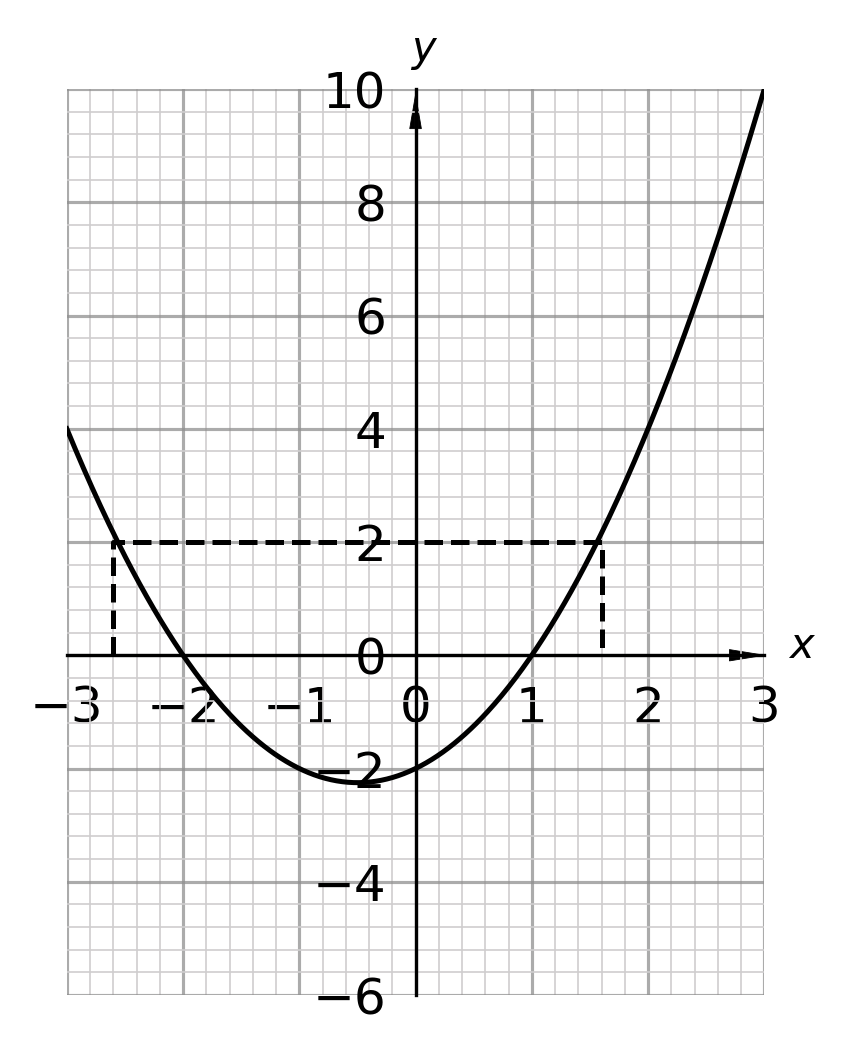
2 marks
Q6
A force of 600 N acts on an area of 20 m^2
The force is increased by 150 N
The area is doubled
Juan says,
“The pressure has decreased by more than 35\%“
Is Juan correct?
Use the equation \text{Pressure} = \dfrac{\text{Force}}{\text{Area}} to justify your answer.
Answer type: multiple choice
Answer: Yes
Wrong Answer: No
Workings:
Originally, the pressure is \dfrac{600}{20}=30 N/m^2
The new pressure is \dfrac{750}{40}=18.75 N/m^2
The percentage change (decrease) is given by,
\dfrac{30-18.75}{30}\times100=37.5\% which is more than 35\% so Juan is correct
3 marks
Q7
Shape Q is enlarged by a scale factor of \dfrac{1}{2} centre (2, 1) to give the new shape P.

Which of the following diagrams correctly displays this enlargement.
Answer type: multiple choice
Answer: 
Wrong Answers:



Workings:
2 marks
Q8
50 people were asked if they prefer action, comedy or thriller films.
27 of the people were female.
7 of the 18 people that said action were male.
10 females said comedy.
10 people said thriller.
One of the males is chosen at random.
What is the probability that this male said thriller?
Give your answer as a fraction in its simplest form.
Answer type: fraction
Answer: 4/23
Workings:
There are 27 females and hence 23 males.
7 males like action, so the remaining 11 people that said action are female.
10 females said comedy, so the females that said thriller is 27-11-10=6
Therefore 4 males said thriller as 10 people said thriller in total.
The number of males that said comedy is 23-7-4=12
A frequency tree to represent this information is shown below.

Reading from the diagram, the probability that a male chosen at random said thriller is \dfrac{4}{23}
4 marks
Q9
Michael buys a house for £200,000
In the first year the price increases by x\%
At the end of the first year the value of the house is £202400
In the second year, the value increases at a rate of 2x\%
What is the value of the hosue at the end of 2 years?
Give your answer to the nearest pound (£).
Answer type: simple
Answer: £207258
Workings:
The percentage increase in value after one year is,
202400 \div 200000=1.012 = 1.2%The rate of value increase during the second year is then 1.2\times2=2.4 \%
The value of the house at the end of the second year is,
202400\times1.024=£207257.60 which is £207258 to the nearest pound.
4 marks
Q10
The vector \textbf{i} and the vector \textbf{j} are shown on the grid.

10(a)
Which of the following diagrams shows the vector -\dfrac{3}{2}\textbf{i}
Answer type: multiple choice
Answer:

Wrong Answers:



Workings:
The vector \textbf{i} may be written as the column vector \begin{pmatrix} 2 \\ -2\end{pmatrix}
Therefore the vector -\dfrac{3}{2}\textbf{i} may be written as \begin{pmatrix} -3 \\ 3\end{pmatrix}
In other words, the arrow is 3 squares long and 3 squares tall, pointing in the opposite direction to the original vector \textbf{i}
1 mark
10(b)
Work out \textbf{i} - 2\textbf{j} as a column vector.
Select the correct option below
Answer type: multiple choice
Answer: \begin{pmatrix} -2 \\ -2 \end{pmatrix}
Wrong Answers:
\begin{pmatrix} -2 \\ 2 \end{pmatrix}
\begin{pmatrix} 0 \\ -2 \end{pmatrix}
\begin{pmatrix} -2 \\ 0 \end{pmatrix}
Workings:
\textbf{i} may be written as the column vector \begin{pmatrix} 2 \\ -2\end{pmatrix}
\textbf{j} may be written as the column vector \begin{pmatrix} 2 \\ 0\end{pmatrix}
So \textbf{i} - 2\textbf{j} may be written as,
\begin{pmatrix} 2 \\ -2\end{pmatrix}-2\begin{pmatrix} 2 \\ 0\end{pmatrix}=\begin{pmatrix} 2-4 \\ -2-0\end{pmatrix} = \begin{pmatrix} -2 \\ -2\end{pmatrix}
2 marks
Q11
f and g are functions such that
f(x)=\dfrac{x^2}{3}\quad and \quad g(x) = 3x^3
11(a)
Find f(-3)
Answer type: simple
Answer: 3
Workings:
f(-3) = \dfrac{(-3)^2}{3}=\dfrac{9}{3}=31 mark
11(b)
Find fg(-1)
Answer type: simple
Answer: 3
Workings:
fg(x) = \dfrac{(3x^3)^2}{3} = \dfrac{9x^6}{3}=3x^6
fg(-1) = 3\times(-1)^6 = 3\times1 = 3
2 marks
Q12

The graphs of y against x represent four different proportionality relationships.
Match each proportionality relationship to the corresponding graph.
You should give your answers as a single capital letter.
Answer type: multiple answers
Answers:
y \propto \dfrac{1}{x} = D
y \propto x^2 = A
y \propto \dfrac{1}{2x} = C
y \propto x^4 = B
Workings:
Graph A and Graph B are very similar. The shape is roughly the same, however Graph B rises more steeply, hence y \propto x^4 = B and y \propto x^2 = A
Graph C and Graph D are very similar. The shape is also roughly the same however Graph C flattens out more quickly as x increases, so y \propto \dfrac{1}{2x} = C and y \propto \dfrac{1}{x} = D
2 marks
Q13

A, B, C and D are points on the circumference of a circle, centre O.
13(a)
Give an equation for y in terms of x
Select the correct option.
Answer type: multiple choice
Answer: y= 120-x
Wrong Answers:
y=120+x y=180-x y=180+2xWorkings:
ABCD is a cyclic quadrilateral, so x+BCD=180\degree,
Hence BCD = 180-x
Angle BOD = 2x as the angle at the centre is twice the angle at the circumference.
The angles in any quadrilateral sum to 360 \degree so for the quadrilateral OBCD,
360 = 2x+60+(180-x)+y
360=x+240+y
120=x+y
y=120-x
3 marks
13(b)
Harold was asked to give the values for x and y.
He said,
“y could be 40 and x could be 80“
Harold is wrong.
Give the values of x and y
Answer type: multiple answers
Answers:
x = 60
y = 60
Workings:
ABD is an equilateral triangle, therefore x=60
y=120-x=120-60=601 mark
Q14
The distance-time graph shows information about part of a car journey.

Use the graph to estimate the speed of the car at time 6 seconds.
Answer type: simple
Answer: 7 m/s
Workings:
\text{speed}=\dfrac{\text{distance}}{\text{time}}=\dfrac{42}{6}=7 m/s
3 marks
Q15
A basketball team is playing in a tournament featuring two matches in the opening rounds.
The probability that the team wins the first match is 0.6
If they win their first match, the probability that they will win the second match is 0.64
If the do not win their first match, the probability that they will win the second match is 0.49
(a) Complete the tree diagram by giving the values of a, b, c, d and e

Answer type: multiple answers
Answers:
a = 0.4
b = 0.64
c = 0.36
d = 0.49
e = 0.51
Workings:
a=1-0.6=0.4
c=1-0.64=0.36
e=1-0.49=0.51
2 marks
(b)
Find the probability that the team will win one of the two matches.
Give your answer to 3 decimal places.
Answer type: simple
Answer: 0.412
Workings:
\text{P(win, not win)} = 0.6\times0.36 = 0.216
\text{P(not win, win)} = 0.4\times0.49=0.196
\text{P(win once)} = 0.216 + 0.196=0.412
3 marks
Q16
16(a)
Select the graph that corresponds to the equation x^2+y^2=16
Answer type: multiple choice
Answer:

Wrong Answers:



Workings:
The equation x^2+y^2=16 is a circle graph with radius =4 and centre origin
2 marks
16(b)
Using your answer from part (a), estimate the solutions of the simultaneous equations
x^2+y^2=16
2y-x=1
Select the closest estimate.
Answer type: multiple choice
Answer: \begin{array}{cc}x_1 = -3.8, & y_1 = -1.4 \\ x_2 = 3.4, & y_2 = 2.2\end{array}
Wrong Answers:
\begin{array}{cc}x_1 = 2.8, & y_1 = -1.4 \\ x_2 = -2.4, & y_2 = 2.2\end{array}
\begin{array}{cc}x_1 = -2.8, & y_1 = -0.4 \\ x_2 = 2.4, & y_2 = 3.2\end{array}
\begin{array}{cc}x_1 = -4.5, & y_1 = -3.5 \\ x_2 = 2.2, & y_2 = 2.9\end{array}
Workings:
Rearranging the second equation,
2y-x=1
2y=x+1
y=0.5x+0.5
Plotting this line on the same graph as the equation x^2+y^2=16,

As can be seen on the plotted graph, the intersections are approximately
\begin{array}{cc}x_1 = -3.8, & y_1 = -1.4 \\ x_2 = 3.4, & y_2 = 2.2\end{array}3 marks
Q17
The histogram shows information about the time taken by some commuters to travel to work.

(a) Complete the frequency table for this information.

Answer type: multiple answers
Answers:
10 \lt t \leq 20 = 13
20 \lt t \leq 40 = 12
40 \lt t \leq 55 = 3
55 \lt t \leq 60 = 3
Workings:
\text{frequency}=\text{class width}\times\text{freq. density}
Hence the frequency in each class is,
10 \lt t \leq 20 = 1.3\times10=13
20 \lt t \leq 40 = 0.6\times20=12
40 \lt t \leq 55 = 0.2\times15=3
55 \lt t \leq 60 = 0.6\times5= 3
2 marks
(b)
Find an estimate for the upper quartile of the time taken to travel to work.
Answer type: multiple choice
Answer: 35
Wrong Answers:
45
40
20
Workings:
Number of commuters, n=39
The position upper quartile is given by \dfrac{3(n+1)}{4} = \dfrac{3(39+1)}{4}=30
Hence the upper quartile is the 30^{\text{th}} commuter.
This falls \dfrac{9}{12}=\dfrac{3}{4} of the way into the 20 \lt t \leq 40 class,
20+(\dfrac{3}{4}\times20)=20+15=35Thus the upper quartile can be estimated as 35.
2 marks
Q18
ABCDEFGH is a cuboid.

EH=12 cm
AF=13cm
Angle ADF=51\degree
Find the size of angle ACD.
Give your answer to the nearest degree.
Answer type: simple
Answer: 41 \degree
Workings:
First, consider the triangle ADF
Let angle AFD = x

Step 1
First, work out the value of x,
x=180-90-51=39
Step 2
Apply the sine rule to work out the length AD
\begin{aligned}\dfrac{AD}{\text{sin}39} &=\dfrac{13}{\text{sin}51} \\[1.2em] AD &= \dfrac{13\text{sin}39}{\text{sin}51} \\[1.2em] AD &= 10.527... \text{cm} \end{aligned}
Step 3
Consider the triangle ACD
Let angle ACD=y
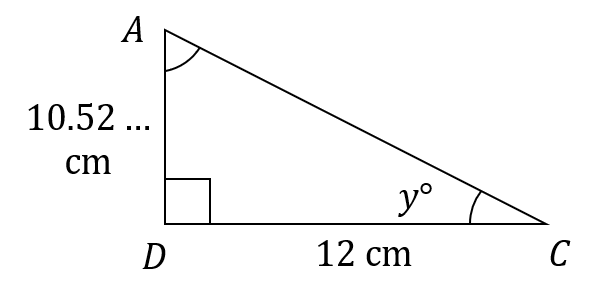
Apply the tan formula to calculate y
\begin{aligned} \text{tan}y &=\dfrac{10.527...}{12} \\[1.2em] y &= \text{tan}^{-1}\bigg(\dfrac{10.527..}{12}\bigg) \\[1.2em] y &= 41.26\end{aligned}
Hence, angle ACD = 41 \degree to the nearest degree.
4 marks
Q19
Shape Q is three quarters of a solid sphere, centre O.

The volume of shape Q is 512\pi cm^3
Find the surface area of Q.
Give your answer correct to 3 significant figures.
Volume of a sphere =\dfrac{4}{3} \pi r^3
Surface area of a sphere = 4\pi r^2
Where r is the radius of the sphere.
Answer type: simple
Answer: 804 cm^2
Workings:
The volume, V, of Q is \dfrac{3}{4} of the volume of a sphere,
V= \dfrac{3}{4}\times\dfrac{4}{3} \pi r^3 = \pi r^3Substituting in the volume of Q and rearranging to work out the value of r,
\begin{aligned}\pi r^3 &= 512\pi \\ r^3 &= 512 \\ r &= 8 \end{aligned}
The surface area, A, of Q is \dfrac{3}{4} of the surface area of a sphere, plus the surface area of two semi-circles,
\begin{aligned} A &= \dfrac{3}{4}\times4\pi r^2 +\dfrac{1}{2}\pi r^2 +\dfrac{1}{2}\pi r^2 \\[1.2em] A &= 3\pi r^2 + \pi r^2 \\[1.2em] A &= 4\pi r^2 \end{aligned}Substituting in the value of r=8,
A=4\pi \times8^2 = 256\pi = 804.2477... cm^2
Hence the surface area of Q is 804 cm^2 to three significant figures.
5 marks
20
(a)
Amir did this question.

Here is how he answered the question.
\begin{aligned} \dfrac{18}{4+\sqrt{7}} &= \dfrac{18}{4+\sqrt{7}} \times \dfrac{4+\sqrt{7}}{4-\sqrt{7}}\\[1.5em] &=\dfrac{72+18\sqrt{7}}{16-4\sqrt{7}+4\sqrt{7}-7} \\[1.5em] &= \dfrac{72+18\sqrt{7}}{9} \\[1.5em] &=8+2\sqrt{7} \end{aligned}
Amir’s answer is wrong.
Identify Amirs mistake.
Answer type: multiple choice
Answer: He should have multiplied the fraction by \dfrac{4-\sqrt{7}}{4-\sqrt{7}}
Wrong Answers:
He should have left the denominator as 9 instead of cancelling the fraction
The denominator should be 8 instead of 9
He should have multiplied the fraction by \dfrac{4+\sqrt{7}}{4+\sqrt{7}}
Workings:
He should have multiplied the fraction by \dfrac{4-\sqrt{7}}{4-\sqrt{7}} is the correct answer. Doing so gives,
\begin{aligned} \dfrac{18}{4+\sqrt{7}} &= \dfrac{18}{4+\sqrt{7}} \times \dfrac{4-\sqrt{7}}{4-\sqrt{7}}\\[1.5em] &=\dfrac{72-18\sqrt{7}}{16-4\sqrt{7}+4\sqrt{7}-7} \\[1.5em] &= \dfrac{72-18\sqrt{7}}{9} \\[1.5em] &=8-2\sqrt{7} \end{aligned}1 mark
(b)
Susan did this question.

Here is how she answered the question.
\begin{aligned} \dfrac{6}{\sqrt{20}} &= \dfrac{6\sqrt{20}}{\sqrt{20}\times\sqrt{20}} \\[1.5em] &= \dfrac{6\sqrt{20}}{20} \\[1.5em] &= \dfrac{6\times4\sqrt{5}}{20} \\[1.5em] &= \dfrac{6\sqrt{5}}{5}\end{aligned}
Susan’s answer is wrong.
Identify Susan’s mistake.
Answer type: multiple choice
Answer: She simplified \sqrt{20} incorrectly; it is not equal to 4\sqrt{5}
Wrong Answers:
She should have multiplied by 5 in the last step to remove the surd.
She should have divided everything by 2 at the start to simplify the calculation.
She should have multiplied everything by 20 at the start.
Workings:
She simplified \sqrt{20} incorrectly; it is not equal to 4\sqrt{5},
\sqrt{20}=\sqrt{4\times5}=\sqrt{4}\times\sqrt{5}=2\sqrt{5}Hence the rest of the working should be,
\begin{aligned}\dfrac{6\sqrt{20}}{20} &= \dfrac{6\times2\sqrt{5}}{20} \\[1.5em] &= \dfrac{12\sqrt{5}}{20} \\[1.5em] &=\dfrac{3\sqrt{5}}{5}\end{aligned}1 mark
Q21
Sampson is trying to find the density of a block of plastic.
The block is in the shape of a cuboid.
He measures,
the length of the block as 12.1 cm, correct to the nearest mm
the width of the block as 10.6 cm, correct to the nearest mm
the height of the block as 8.2 cm, correct to the nearest mm
He measures the mass as 330 g, correct to the nearest 10 g
By considering bounds, work out the minimum and maximum values for the density of the block of plastic.
Give your answers to three significant figures.
Answer type: multiple answers
Answers:
Minimum density = 0.304 g/cm^3
Maximum density = 0.323 g/cm^3
Wrong Answers:
Workings:
Minimum Density:
First, calculate the maximum volume, V_{\text{max}} by using the upper bounds for each of the side lengths of the block:
V_{\text{max}} = 12.15\times10.65\times8.25=1067.529375 cm^3
The minimum mass, m_{\text{min}}=325 g
Therefore minimum density,
d_{\text{min}}=\dfrac{m_{\text{min}}}{V_{\text{max}}}=\dfrac{325}{1067.529375}=0.304 g/cm^3
Maximum Density:
First, calculate the minimum volume, V_{\text{min}} by using the lower bounds for each of the side lengths of the block:
V_{\text{min}} = 12.05\times10.55\times8.15=1036.089125 cm^3
The maximum mass, m_{\text{max}}=325 g
Therefore maximum density,
d_{\text{max}}=\dfrac{m_{\text{max}}}{V_{\text{min}}}=\dfrac{335}{1036.089125}=0.323 g/cm^3
5 marks
