Question 1(a): [1 mark]
Choose which of the following numbers are prime numbers.
Answer type: Multiple choice type 1
A: 5
B: 12
C: 27
D: 7
E: 29
F: 17
G: 2
H: 25
I: 24
J: 18
K: 8
L: 1
M: 16
N: 3
O: 49
P: 125
ANSWER: A: 5, D: 7, E: 29, F: 17, G: 2, N: 3
Question 1(b): [1 mark]
Which of the following is the correct definition for a prime number.
Answer type: Multiple choice type 2
A: A number that can only be divided by 2.
B: A number that is not the square of another number.
C: A number that can be written as a fraction.
D: A number that can only be divided by 1 and itself.
ANSWER: D: A number that can only be divided by 1 and itself.
Question 2(a): [2 marks]
Find the values of a, \, b, \, c in the prime factor tree of 24.
b > c.
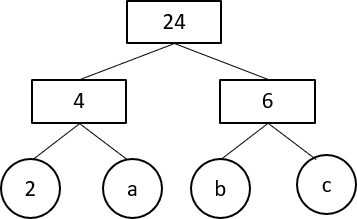
Answer type: Multiple answers type 1
ANSWER: a = 2, \, b = 3, \, c = 2
WORKING: 4 = 2 \times 2 ; 6 = 3 \times 2
Question 2(b): [2 marks]
Find the values of a, \, b, \, c in the prime factor tree of 50.
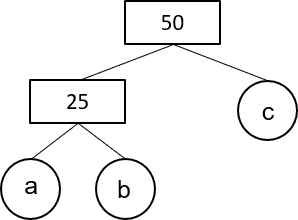
Answer type: Multiple answers type 1
ANSWER: a = 5, \, b = 5, \, c = 2
WORKING: 50 = 25 \times 2 ; 25 = 5 \times 5
Question 2(c): [2 marks]
Find the values of a, \, b, \, c in the prime factor tree of 140.
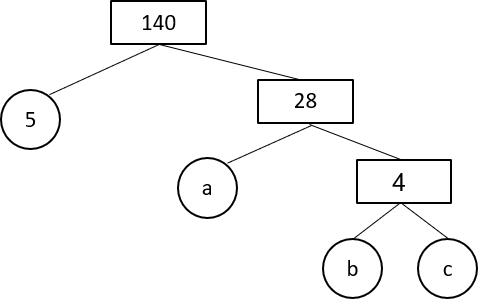
Answer type: Multiple answers type 1
ANSWER: a = 7, \, b = 2, \, c = 2
WORKING: 140 = 28 \times 5
28 = 4 \times 7 ; 4 = 2 \times 2
Question 3(a): [2 marks]
What is the correct answer for 72, written as a product of its prime factors in index form.
Answer type: Multiple choice type 1
A: 2^2 \times 3^3
B: 2^3 \times 3^2
C: 2 \times 3^3
D: 2 \times 3^2 \times 7
ANSWER: B: 2^3 \times 3^2
WORKING: 72 = 2 \times 2 \times 2 \times 3 \times 3 = 2^3 \times 3^2
Question 3(b): [2 marks]
What is the correct answer for 90, written as a product of its prime factors in index form.
Answer type: Multiple choice type 1
A: 2^2 \times 5^2
B: 2^2 \times 3 \times 5
C: 2 \times 5 \times 7
D: 2 \times 3^2 \times 5
ANSWER: D: 2 \times 3^2 \times 5
WORKING: 90 = 2 \times 3 \times 3 \times 5 = 2 \times 3^2 \times 5
Question 3(c): [2 marks]
What is the correct answer for 160, written as a product of its prime factors in index form.
Answer type: Multiple choice type 1
A: 2^5 \times 5
B: 2^4 \times 5
C: 2^3 \times 5^2
D: 2^6 \times 3
ANSWER: A: 2^5 \times 5
WORKING: 160 = 2 \times 2 \times 2 \times 2 \times 2 \times 5
Question 4(a): [2 marks]
What is the correct answer for 1620, written as a product of its prime factors in index form.
Answer type: Multiple choice type 1
A: 2^3 \times 3^3 \times 5
B: 2^2 \times 3^3 \times 5 \times 7
C: 2^2 \times 3^4 \times 5
D: 2^6 \times 5 \times 7
ANSWER: C: 2^2 \times 3^4 \times 5
WORKING: 1620 = 2 \times 2 \times 3 \times 3 \times 3 \times 3 \times 5 = 2^2 \times 3^4 \times 5
Question 4(b): [2 marks]
What is the correct answer for 420, written as a product of its prime factors in index form.
Answer type: Multiple choice type 1
A: 2^2 \times 3 \times 5 \times 7
B: 2 \times 3^2 \times 5 \times 7
C: 2 \times 3^2 \times 5^2
D: 2 \times 3 \times 5 \times 7
ANSWER: A: 2^2 \times 3 \times 5 \times 7
WORKING: 420 = 2 \times 2 \times 3 \times 5 \times 7 = 2^2 \times 3 \times 5 \times 7
Question 4(c): [1 mark]
Find the HCF of 1620 and 420.
Answer type: Simple text answer
ANSWER: 60
WORKING:
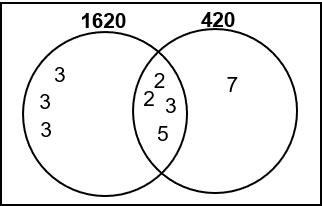
HCF = 2 \times 2 \times 3 \times 5 = 60.
Found by multiplying the factors from the centre of the Venn diagram.
Question 4(d): [1 mark]
Find the LCM of 3 and 7.
Answer type: Simple text answer
ANSWER: 21
WORKING: 3 \times 7 = 21
Question 5: [4 marks]
Find the HCF and LCM of 126 and 234.
Answer type: Multiple answers type 1
ANSWER: HCF = 18, LCM = 1638
WORKING: 126 = 2 \times 3 \times 3 \times 7 = 2 \times 3^2 \times 7
234 = 2 \times 3 \times 3 \times 13 = 2 \times 3^2 \times 13
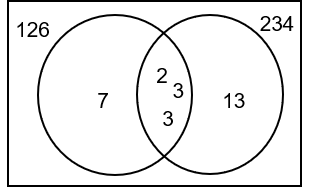
HCF = 2 \times 3 \times 3 = 18
Found by multiplying the factors from the centre of the Venn diagram.
LCM = 2\times 3 \times 3 \times 7 \times 13 = 1638.
Found by multiplying all the factors from the Venn diagram.
Question 6: [3 marks]
x and y are two positive numbers greater than 21.
The HCF of x and y is 21.
The LCM of x and y is 210.
x < y.
Find x and y.
Answer type: Multiple answers type 1
ANSWER: x = 42, y = 105.
WORKING:
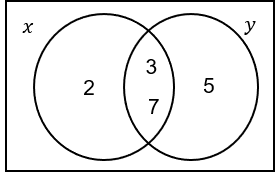
x = 2 \times 3 \times 7 = 42
Found by multiplying the factors from the x part (the left circle) of the Venn diagram.
y = 3 \times 7 \times 5 =105
Found by multiplying the factors from the y part (the right circle) of the Venn diagram.
Question 7: [3 marks]
Choose the correct HCF and LCM of 10a^2b^3c and 5ab^2cd.
Answer type: Multiple choice type 2
A: HCF = 5ab^2c, LCM = 10a^2b^3cd
B: HCF = 5abc, LCM = 10a^2b^3cd
C: HCF = 5ab^2c, LCM = 10ab^3cd
D: HCF = 5ab^2c, LCM = 10a^2b^2cd
ANSWER: A: HCF = 5ab^2c, LCM = 10a^2b^3cd
WORKING:
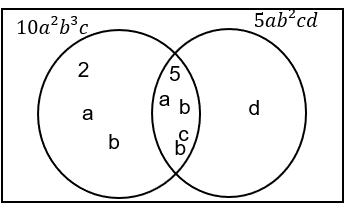
HCF = 5 \times a \times b \times b \times c = 5ab^2c
Found by multiplying the factors from the centre of the Venn diagram.
LCM = 2 \times a \times b \times 5 \times a \times b \times b \times c \times d = 10a^2b^3cd
Found by multiplying all the factors from the Venn diagram.
