Question 1
Consider the following inequalities.
1(a):
Factorise x^2-4x+3
ANSWER: Multiple Choice (Type 1)
A: (x-4)(x-3)
B: (x-2)(x-1)
C: (x-2)(x-4)
D: (x-3)(x-1)
Answer: D
Workings:
Need two numbers with a product of 3 and sum of -4.
These can only be -3 and -1, so factorisation is (x-3)(x-1)
Marks= 2
1(b):
Choose the graph that solvesx^2-4x+3<0 graphically.
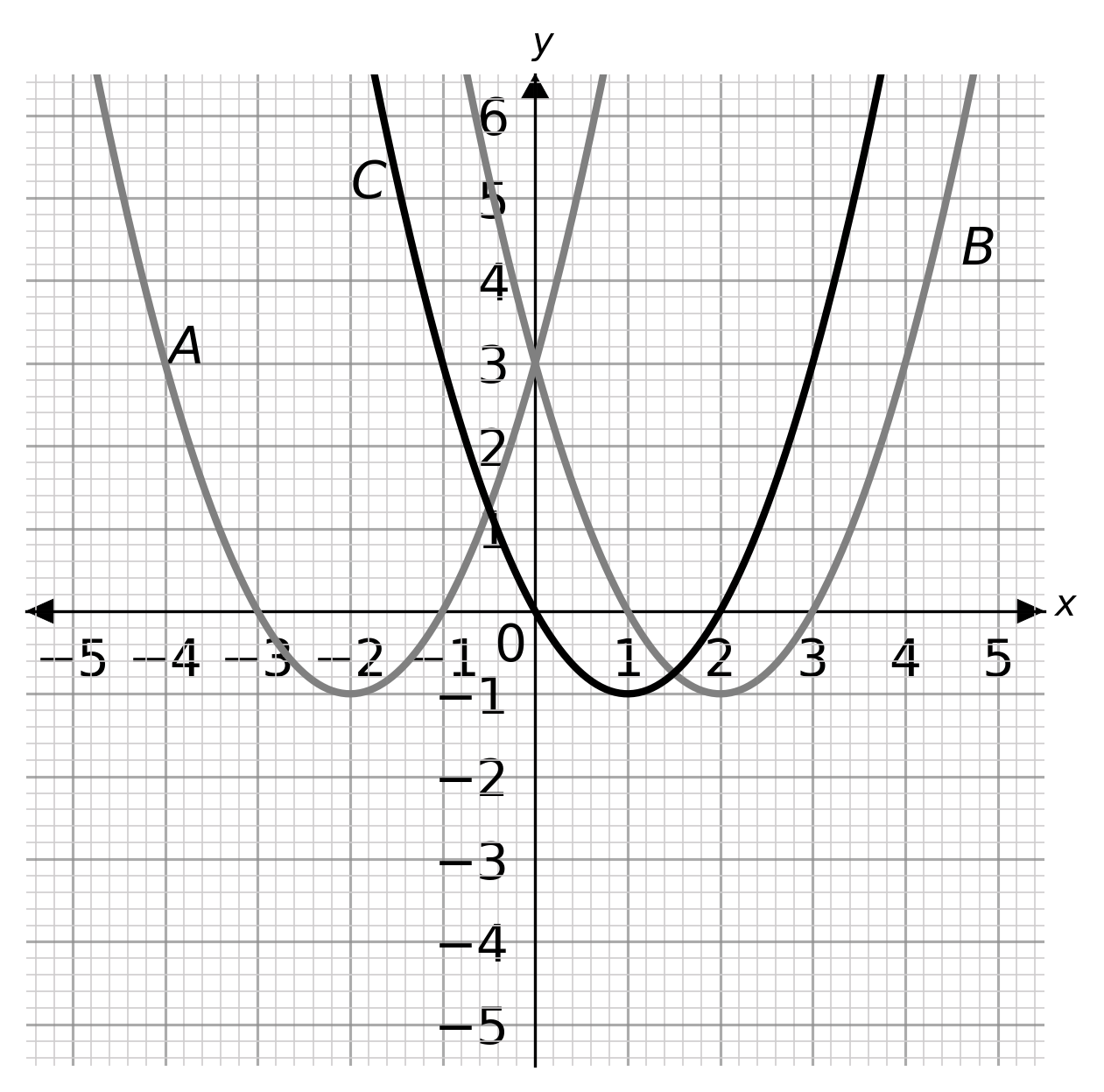
ANSWER: Multiple Choice (Type 1)
A: -3 < x < -1
B: 1 < x < 3
C: 0 < x < 2
Answer: B
Workings:
(x-3)(x-1)=0 when x=3 and x=1. These are the points the graph intersects with the x-axis.
(x-3)(x-1) < 0 between x=1 and x=3.
The inequality is solved for 1 < x < 3.
Marks = 2
Question 2
Consider the following inequalities.
Question 2(a):
Factorise x^2 + 5x + 4.
Answer: Multiple Choice (Type 1)
A: (x+2)(x+3)
B: (x+4)(x+1)
C: (x+5)(x+4)
D: (x+3)(x+6)
Answer: B
Workings:
Need two numbers with a product of 4 and a sum of 5.
These can only be 1 and 4 so factorisation is (x+4)(x+1).
Marks = 2
Question 2(b)
Choose the graph that solves x^2+5x+4 > 0 graphically.
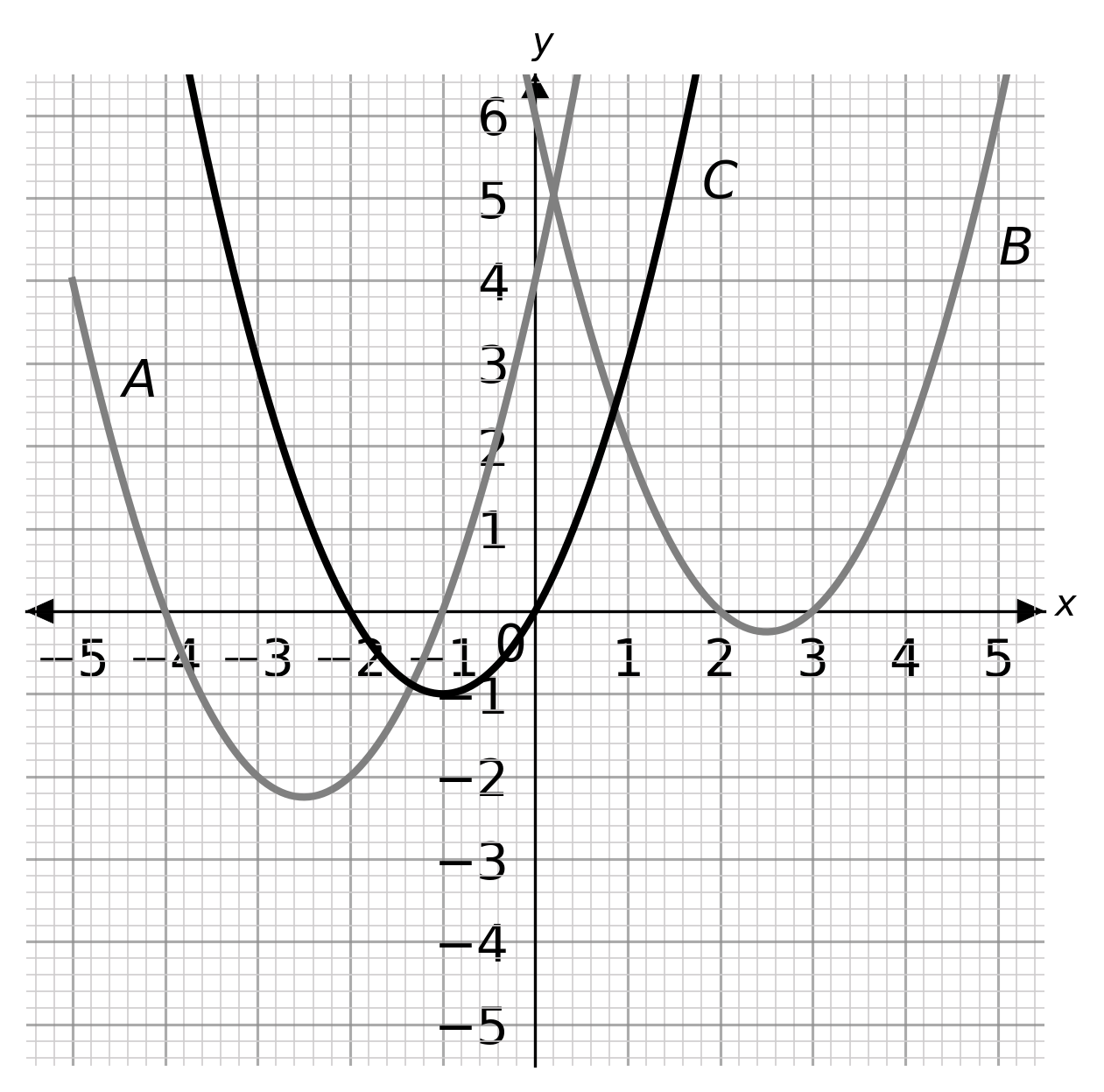
ANSWER: Multiple Choice (Type 1)
A: x<-4 and x>-1
B: x<2 and x>3
C: x<-2 and x>0
Answer: A
Workings:
(x+4)(x+1)=0 when x=-4 or x=-1. These are the points the graph intersects with the x axis.
(x+4)(x+1) > 0 when x is less than -4 and more than -1.
(x+4)(x+1) > 0 when x < -4 and x > -1.
Marks = 2
Question 3
Consider the following inequalities.
3(a):
Factorise 6x^2+48x+90.
ANSWER: Multiple Choice (Type 1)
A: (x+1)(x+5)
B: (x+2)(x+4)
C: (x+1)(x+3)
D: (x+3)(x+5)
Answer: D
Workings:
\dfrac{6x^2+48x+90}{6} = x^2+8x+15
=(x+3)(x+5)
Marks = 3
3(b):
Choose the graph that displays 6x^2+48x+90\geq 0.
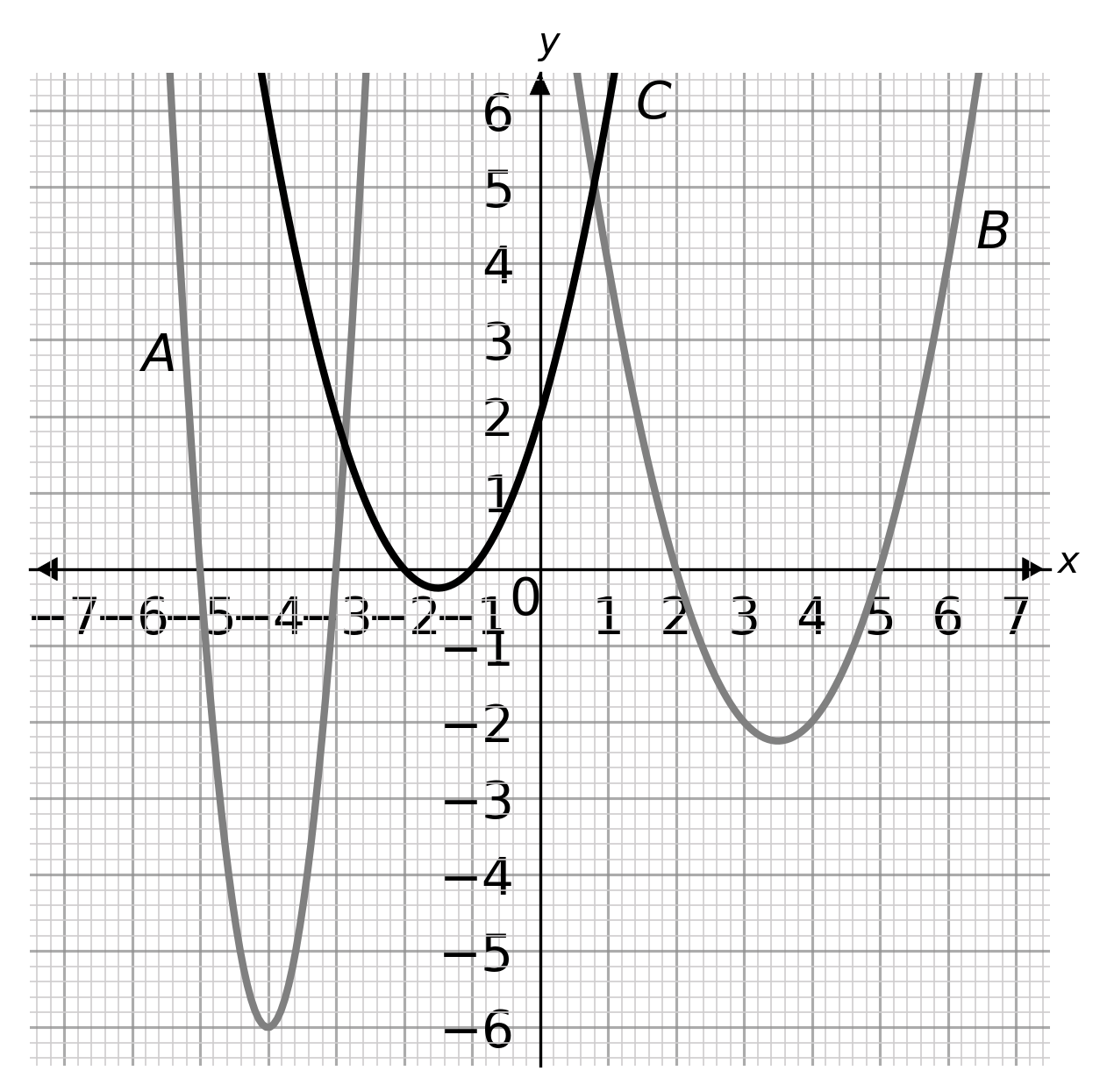
ANSWER: Multiple Choice (Type 1)
A: x\leq -5 and x\geq -3
B: x\leq -2 and x\geq -1
C: x\leq 2 and x\geq 5
Answer: B
Workings:
When (x+3)(x+5)=0 when x=-3 or x=-5.
(x+3)(x+5)\geq 0 when x is less than or equal to -5 and more than or equal to -3.
(x+3)(x+5)\geq 0 when x\leq -5 and x\geq -3.
Marks =2
Question 4
Choose the graph that displays x^2-6x+9>0.
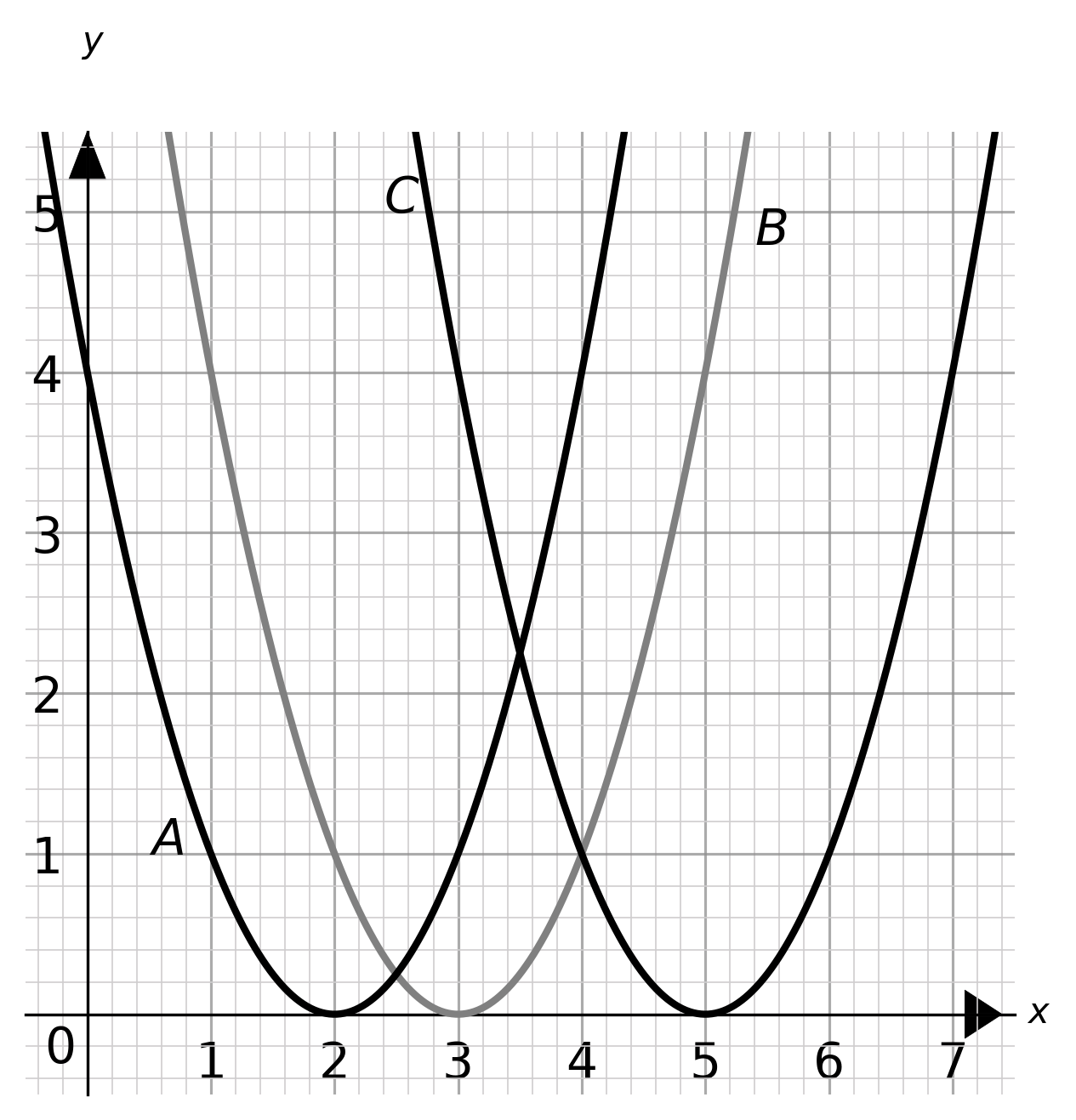
ANSWER: Multiple Choice (Type 1)
A: x < 2 and x > 2
B: x < 3 and x > 3
C: x < 5 and x > 5
Answer: B
Workings:
Factorise x^2-6x+9 to (x-3)(x-3).
(x-3)(x-3)=0 when x=3 only.
This means the graph only has one intersection point with the x axis.
(x-3)(x-3) > 0 when x < 3 and x > 3.
Marks = 2
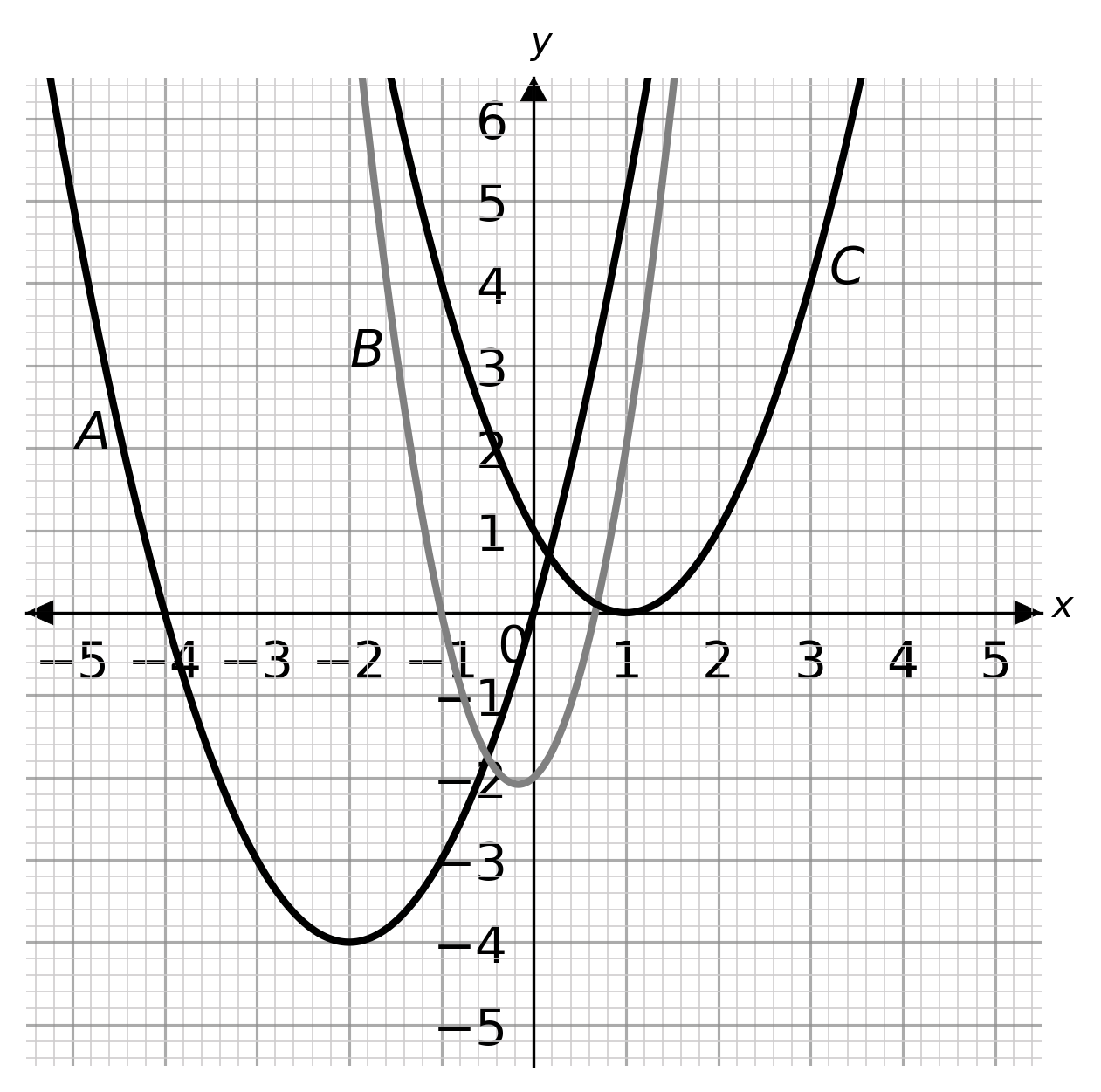
Question 5
Choose the graph that displays 2x^2+3x-2 > 0.
ANSWER: Multiple Choice (Type 1)
A: x < -2 and x > -1
B: x < -2 and x > \dfrac{3}{2}
C: x < 1 and x > 5
Answer: B
Workings:
Factorise 2x^2+3x-2 to (2x-1)(x+2).
(2x-1)(x+2)=0 when x=\dfrac{1}{2} and x=-2.
(2x-1)(x+2) > 0 when x < -2 and x > \dfrac{1}{2}.
Marks = 4
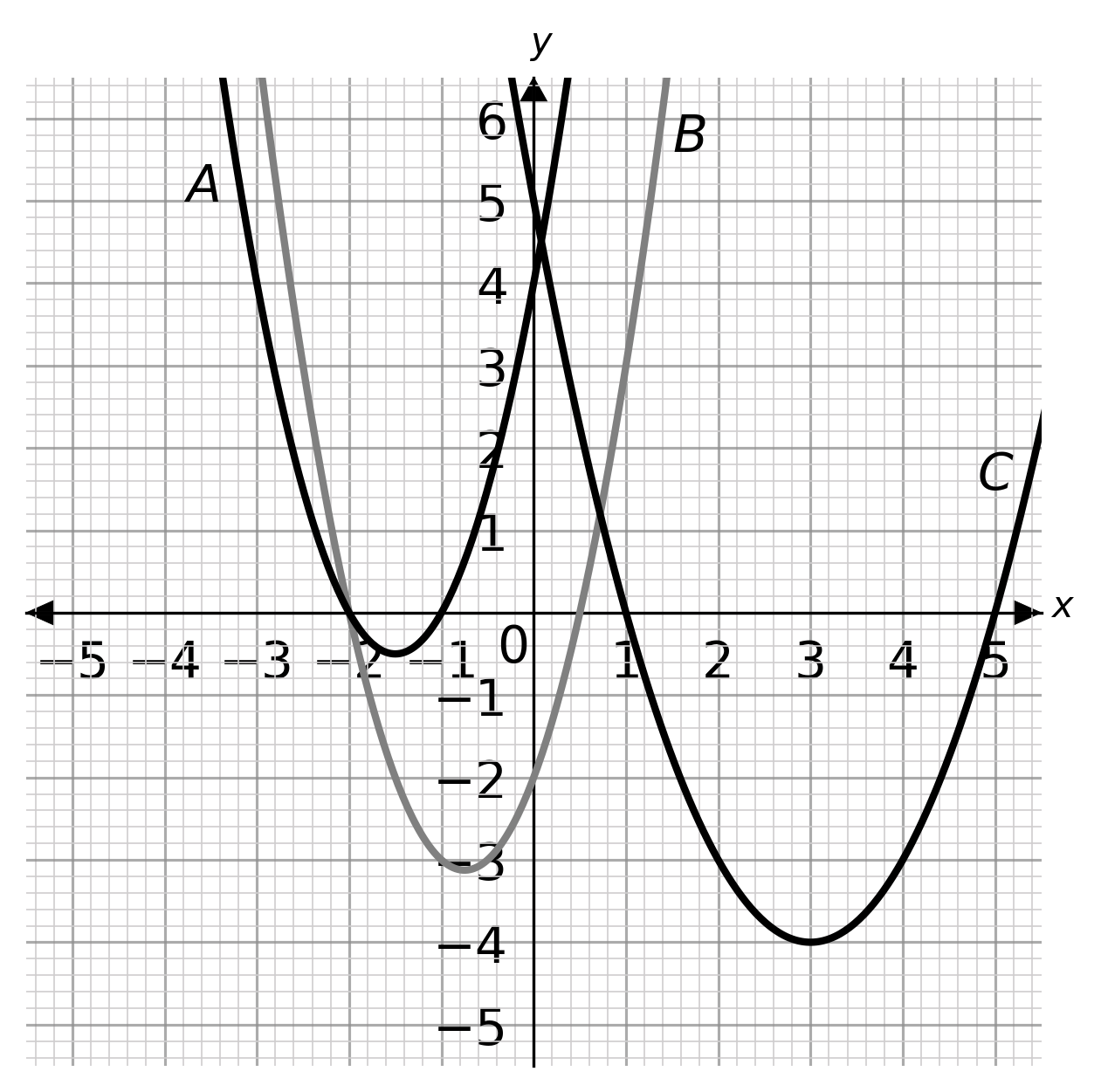
Question 6
Choose the graphs that show the inequalities x^2+4x > 0 and (x+1)(3x-2) > 0.
ANSWER: Multiple Choice (Type 1)
A: A and B: x < -4 and x > \dfrac{2}{3}
B: A and C: x < -4 and x > 1
C: B and C: x < -1 and x > 1
Answer: A
Workings:
x(x+4) > 0 and (x+1)(3x-2) > 0
x(x+4) > 0 when x < -4 and x > 0.
(x+1)(3x-2) > 0 when x < -1 and x > \dfrac{2}{3}
The x values that satisfy both inequalities are x < -4 and x > \dfrac{2}{3}.
Marks = 6
