Question 1
Consider the following quarter-circle with centre O.
The radius is 3.6 m.

Find the area of the quarter-circle.
Give your answer to 2 decimal places in m^2.
ANSWER: Simple Text Answer
Answer: 10.18
Workings:
A = \dfrac{1}{4}\times \pi \times (3.6)^2
Area = 10.18 m^2
Marks = 3
Question 2
The diagram shows the sector of a circle with centre O
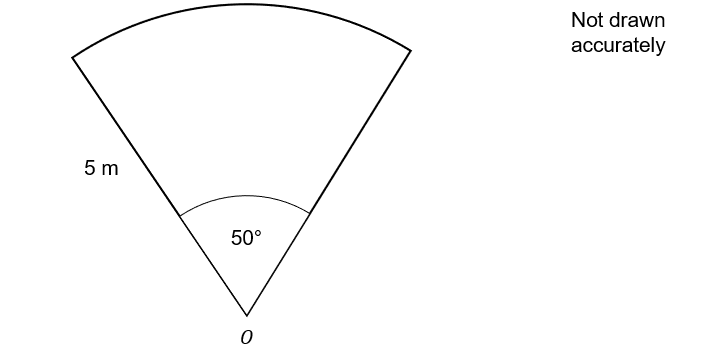
The radius of the circle is 5 m and the angle of the sector is 50°
Calculate the area of the sector.
Give your answer to one decimal place in m^2.
ANSWER: Simple Text Answer
Answer: 10.9
Workings:
Area of Sector = \dfrac{x}{360}\times Area of full Circle
Area of Sector = \dfrac{50}{360}\times \pi \times 5^2 = 10.9 m^2
Marks = 3
Question 3
The diagram shows the sector of a circle with centre O.
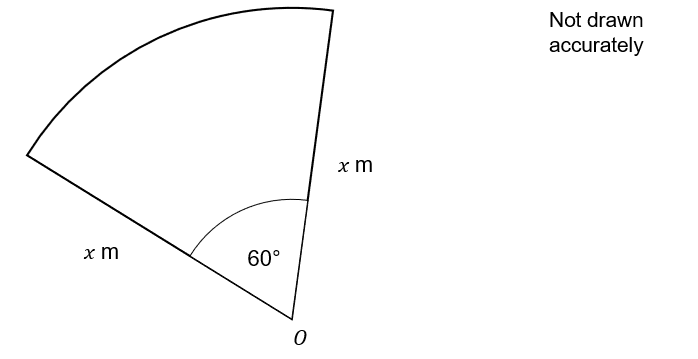
The area of the sector is 18.4 m^2 to 1 decimal place and the angle is 60°
Calculate the radius of the sector.
Give your answer to one decimal place in metres.
ANSWER: Simple Text Answer
Answer: 5.9
Workings:
Area of Sector = \dfrac{Angle}{360} \times \pi \times x^2
Rearrange to get
x = \sqrt{\dfrac{360\times Area of Sector}{Angle\times \pi}}
x = \sqrt{\dfrac{360\times 18.4}{60\times \pi}}
x = 5.9 m
Marks = 3
Question 4
The sector of a circle below has a radius of 5m and the angle at the centre is 30°

4(a):
Find the area of the sector.
Give your answer to one decimal place in m^2.
ANSWER: Simple Text Answer
Answer: 6.5 m^2
Workings:
Area of Sector = \dfrac{x}{360} \times Area of full Circle
Area of Sector = \dfrac{30}{360}\times \pi \times 5^2
Area of Sector = 6.5 m^2
Marks = 2
4(b):
Find the arc length of the sector.
Give your answer to one decimal place in metres.
ANSWER: Simple Text Answer
Answer: 2.6
Workings:
Length of Arc = \dfrac{x}{360}\times Circumference of full Circle
Length of Arc = \dfrac{30}{360}\times \pi \times 10
Length of Arc = 2.6
Marks = 2
Question 5
The area of the sector below is 26.14 m^2

Calculate the value of the angle x
Give your answer to one decimal place.
ANSWER: Multiple Choice Answer
A: 36.0\degree
B: 36.5\degree
C: 37.0\degree
D: 37.5\degree
Answer: C
Workings:
Area of Sector = \dfrac{x}{360}\times Area of full Circle
Rearrange to get
x = \dfrac{360 \times Area of Sector}{\pi \times 9^2}
x = 37.0\degree
Marks = 2
Question 6
The diagram shows an equilateral triangle with side lengths of 9 cm
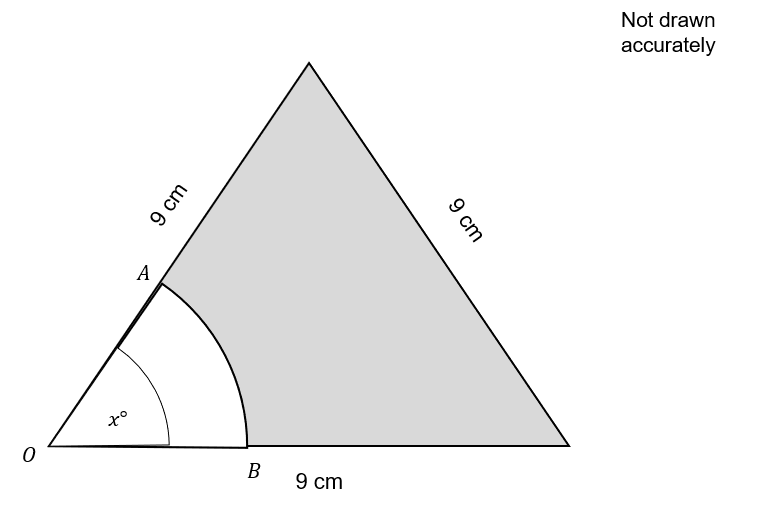
Given O is the centre of a circle and OAB is a sector of that circle where OA = 3 cm
Find the perimeter of the shaded region.
Give your answer to one decimal place in metres.
ANSWER: Simple Text Answer
Answer: 24.1
Workings:
Length of Arc = \dfrac{x}{360}\times Circumference of full Circle
Length of Arc = \dfrac{60}{360}\times \pi \times 6
Length of Arc = \pi
Summing all the sides together gives
9 + 6 + 6 + 3.1 = 24.1 cm
Marks = 3
Question 7
OAB is a circle segment of radius 8 cm
O is a circle of radius 4 cm
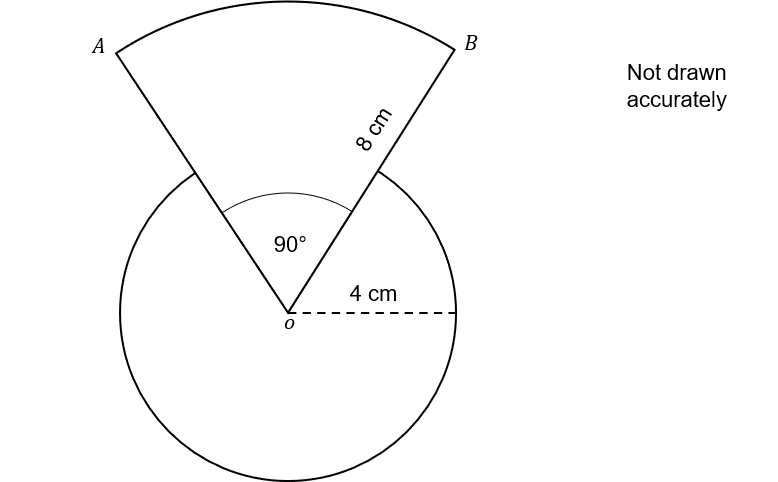
Calculate the total area of the shape shown above.
Give your answer to one decimal place in cm^2.
ANSWER: Simple Text Answer
Answer: 88.0
Workings:
First calculate the area of circle O
\pi \times 4^2 = 16\pi
Calculate the area of the circle segment
\dfrac{90}{360}\times \pi \times 64 = 16\pi
Find the area of the segment that is part of OAB where the arc coincides with the circumference of O.
\dfrac{90}{360}\times \pi \times 4^2 = 4\pi
Find the total area by adding circle O and segment OAB, then subtracting the smaller segment
16\pi + 16\pi - 4\pi = 28\pi = 88.0 cm^2
Marks = 3
