Question 1
The diagram below shows a cylinder.
The radius of the cylinder is 3 cm and the height is 12 cm.
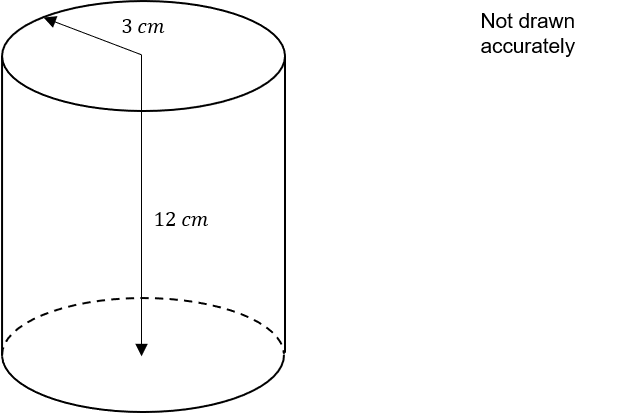
Find the total surface area of the cylinder shown above.
Give your answer to 2 decimal places in cm^2.
ANSWER: Simple Text Answer
Answer: 282.74
Workings:
Calculate the area of the two circular faces
2\times \pi \times 3^2 = 18\pi
Calculate the area of the curved face
2\times \pi \times 3 \times 12 = 72\pi
Adding the two together gives
18\pi + 72\pi = 90\pi = 282.74 cm[latex]^2
Marks = 2
Question 2
The diagram below shows two cuboids, A and B.
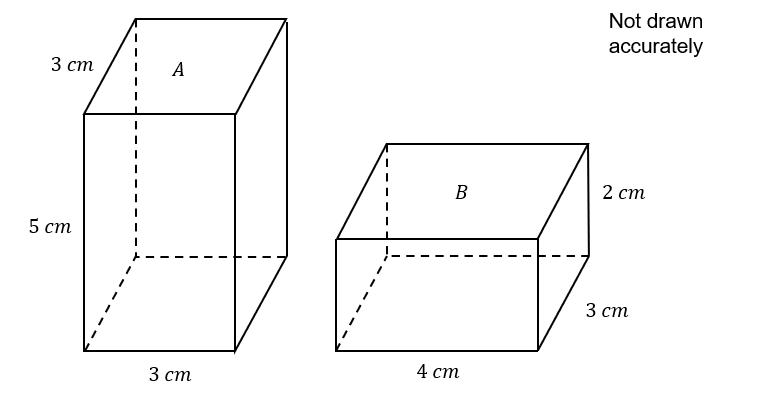
2(a):
Find the combined total surface area of cuboids A and B shown above in cm^2.
ANSWER: Simple Text Answer
Answer: 130
Workings:
Calculate the area of cuboid A
2\times 3\times 5 + 2\times 3\times 5 + 2\times 3\times 3 = 30 + 30 + 18 = 78 cm^2
Calculate the area of cuboid B
2\times 4\times 2 + 2\times 3\times 2 + 2\times 4\times 3 = 16 + 12 + 24 = 52 cm^2
Summing the two cuboids gives
78 + 52 = 130 cm^2
Marks = 2
2(b):
The two cuboids are attached to each other by placing the entire 3\times 2 face of cuboid B onto one face of cuboid A.
Calculate the surface area of the new shape in cm^2.
ANSWER: Simple Text Answer
Answer: 118
Workings:
The new shape will keep the same area except for two overlapping faces of 3 cm\times 2 cm.
The area not included is calculated as
2\times 3\times 2 = 12 cm^2
Subtract this from the total area found in the previous part
130 - 12 = 118 cm^2
Marks = 2
Question 3
The diagram below shows a representation of a small USB drive consisting of two cuboids, ABCDEFHG and IJKLMNOP attached together.
AG=12 mm, BH=3 mm, GF=9 mm
IL=3 mm, KO=1 mm, IJ=e
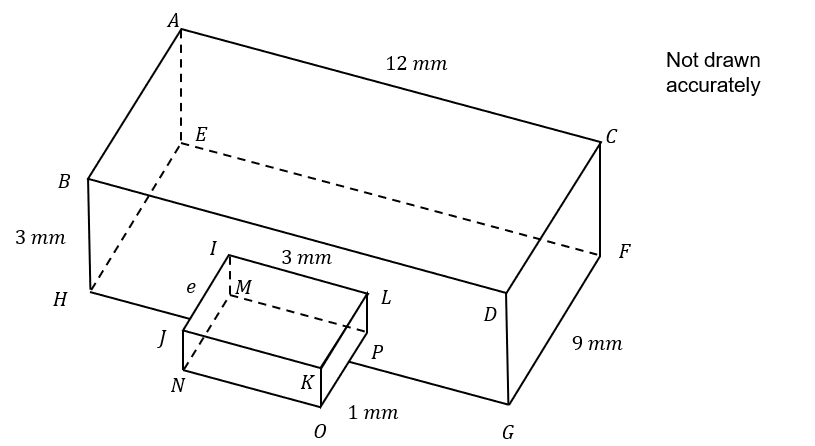
3(a):
Find an expression for the total surface area of the USB drive, in terms of e.
ANSWER: Multiple Choice (Type 1)
A: 342 + 8e
B: 297 + 10e
C: 212 + 7e
D: 389 + 6e
Answer: A
Workings:
First calculate the area of the larger cuboid
2\times 3\times 12 + 2\times 9\times 3 + 2\times 9\times 12 = 342 mm^2
Then calculate the area of the smaller cuboid
2\times 1\times 3 + 2\times 1\times e + 2\times 3\times e = 6 + 8e mm^2
The area lost through overlap can be calculated as
2\times 3\times 1 = 6 mm^2
To find the total surface area, add the two cuboids together, then subtract the overlap area
342 + 6 + 8e - 6 = 342 + 8e
Marks = 4
3(b):
If the total surface area of the drive is 360 mm^2.
Calculate the value of e in mm
ANSWER: Simple Text Answer
Answer: 2.25
Workings:
342+8e = 360
8e = 18
e = 2.25
Marks = 1
Question 4
The diagram below shows a cone.
The radius of the cone is 4 cm and the slanted height is 9 cm.
Use the equations: Surface area = \pi rl+\pi r^2
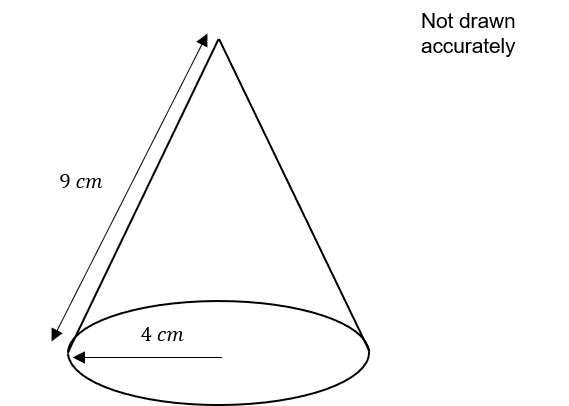
Calculate the total surface area of the cone.
Give your answer to 2 decimal places in cm^2
ANSWER: Simple Text Answer
Answer: 163.36
Workings:
Area of the circular base is
\pi \times 4^2 =16\pi
Curved face can be calculated as
\pi rl = \pi \times 4\times 9 = 36\pi
Adding both faces together gives
16\pi + 36\pi = 52\pi = 163.36 cm^2
Marks = 3
Question 5
The diagram below shows a sphere.
The radius of the sphere is 5 cm.
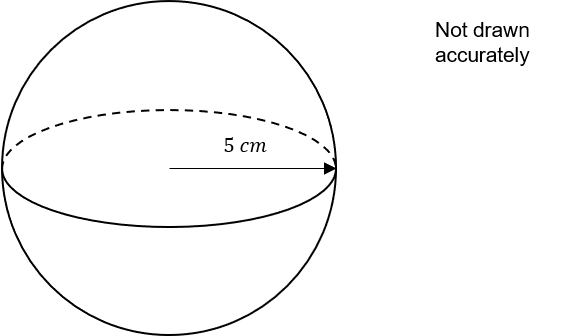
Using the equation A= 4\pi r^2, calculate the surface area of the sphere.
Give your answer to 2 decimal places in cm^2.
ANSWER: Simple Text Answer
Answer: 314.16
Workings:
Substitute the given values into the equation for surface area of a sphere
4\times \pi \times 5^2= 100\pi = 314.16 cm^2
Marks = 2
Question 6
The diagram below shows a triangular prism ABCDEF
CB=6 cm
BE=11 cm
AB = BCThe vertical height = 8 cm
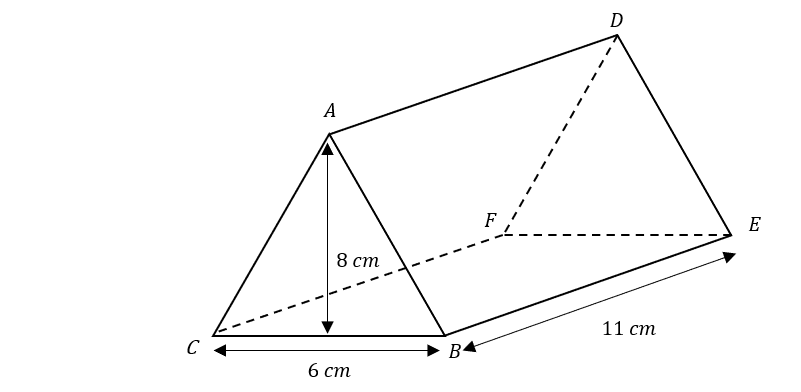
Calculate the surface area of the triangular prism.
Give your answer to 2 decimal places in cm^2
ANSWER: Simple Text Answer
Answer: 301.97
Workings:
Calculate the length of side AB</p> <p style="text-align: left;">[latex]AB = \sqrt{8^2+3^2} = \sqrt{73}
Calculate the area of the rectangular faces
2\times 11\times \sqrt{73} + 6\times 11 = 253.968
Calculate the area of the two triangular faces
2\times \dfrac{1}{2}\times 6\times 8 = 48 cm^2
Add the areas for all the faces together
253.968 + 48 = 301.97 cm^2
Marks = 4
Question 7
A shape is made from a cylinder of radius 5 cm and height 4 cm.
A cuboid measuring 6 cm wide, 1 cm long and 4 cm deep is cut out of the centre as shown below.
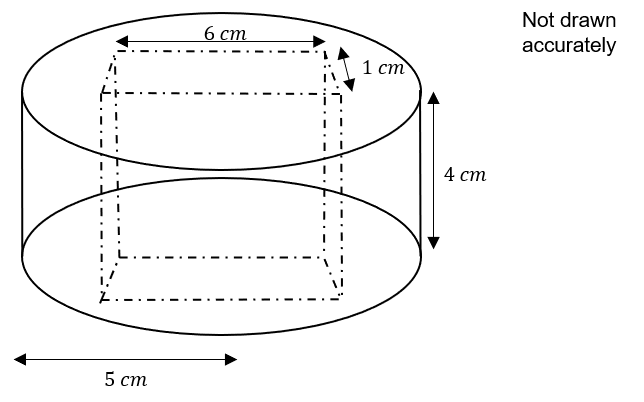
7(a):
Calculate the total surface area of the cylinder before the cuboid was removed.
Give your answer in terms of \pi
ANSWER: Multiple Choice (Type 1)
A: 70\pi
B: 80\pi
C: 90\pi
D: 100\pi
Answer: C
Workings:
Calculate the area of the circular faces
2\times \pi \times 5^2 = 50\pi
Calculate the area of the curved face
2\times \pi \times 5 \times 4 = 40\pi
Add the areas together
50\pi + 40\pi = 90\pi
Marks = 2
7(b):
Calculate the surface area of the new shape formed by removing the cuboid.
Give your answer as a decimal to 2 decimal places in cm^2.
ANSWER: Simple Text Answer
Answer: 326.74
Workings:
The cuboid shares two faces with the cylinder which will be removed
2\times 1\times 6 = 12 cm^2
The other four sides of the cuboid will be added to the total surface area
2\times 1\times 4 + 2\times 6\times 4 = 56 cm^2
The new surface area can be given by
90\pi - 12 + 56 = 326.74 cm^2
Marks = 2
