Question 1: [3 marks]
ABC is a right-angled triangle.
\angle BAC = 30 \degree
AB = 12 cm

Using trigonometry, find the length of the side CB.
Answer type: Simple text answer
ANSWER: 6 cm
WORKING:
\sin (30) = \dfrac{cb}{12}
cb = 12 \sin(30) = 6
Question 2:
DEF is a right-angled triangle.
DE = 5 cm
\angle EDF = 60 \degree
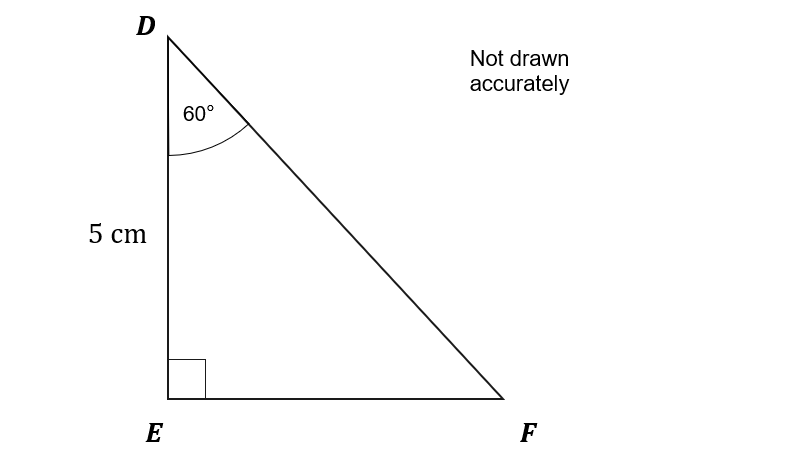
Question 2(a): [3 marks]
Find the length DF.
Answer type: Simple text answer
ANSWER: 10 cm
WORKING:
\cos (60) = \dfrac{A}{H}
DF = \dfrac{DE}{\cos (60)} = \dfrac{5}{\cos (60)} = 10 cm
Question 2(b): [3 marks]
Using your answer to part (a), find the length EF.
Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 8.66 cm
WORKING:
\sin (60) = \dfrac{EF}{10}
EF = 10 \sin (60) = 5\sqrt{3} = 8.66 cm (2 dp)
Question 3:
Below is a right angled triangle.
OP = 6.4 cm
OQ = 9.5 cm

Question 3(a): [3 marks]
Find the size of the angle POQ. Give your answer to 2 significant figures.
Answer type: Simple text answer
ANSWER: 34 \degree
WORKING:
\tan (POQ) = \dfrac{6.4}{9.5}
POQ = \tan^{-1} \bigg(\dfrac{6.4}{9.5} \bigg) = 33.967 = 34 \degree (2 sf)
Question 3(b): [1 mark]
What is the size of angle OPQ?
Answer type: Simple text answer
ANSWER: 56 \degree
WORKING:
\angle OPQ = 180 - 90 - 34 = 56 \degree
Question 4:
ABC is a right-angled triangle
Side AB = 7 cm
Side BC = 4 cm
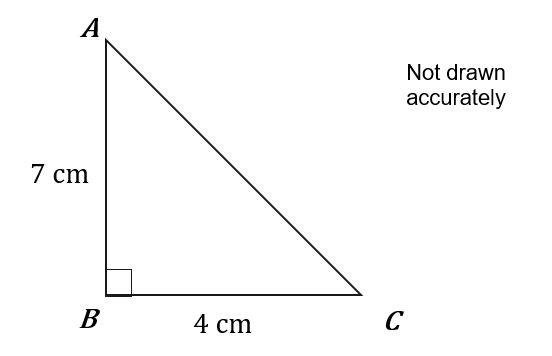
Question 4(a): [3 marks]
Find the size of angle CAB.
Give your answer to 2 significant figures.
Answer type: Simple text answer
ANSWER: 30
WORKING:
\tan (CAB) = \dfrac{4}{7}
CAB = \tan^{-1} \bigg( \dfrac{4}{7} \bigg) = 30 \degree (2 sf)
Question 4(b): [1 mark]
Find the size of angle ACB.
Answer type: Simple text answer
ANSWER: 60 \degree
WORKING:
\angle ACB = 180 - 90 - 30 = 60 \degree
Question 4(c): [2 marks]
Find the side length AC using trigonometry.
Give your answer to 1 significant figures.
Answer type: Simple text answer
ANSWER: 8 cm
WORKING:
\sin (60) = \dfrac{AB}{AC}
AC = \dfrac{7}{\sin (60)} = 8 cm (1 sf)
Question 5:
Below is a rectangle.
Angle DAC is 42 \degree.
Side AC is 5 cm.

Question 5(a): [3 marks]
Find the length of the diagonal line AC.
Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 6.73 cm
WORKING:
\cos (42) = \dfrac{5}{AC}
AC = \dfrac{5}{\cos (42)} = 6.73 cm (2 dp)
Question 5(b): [3 marks]
Using your answer to part (a) find the length DC.
Give your answer to 2 decimal places
Answer type: Simple text answer
ANSWER: 4.50 cm
WORKING:
\sin (42) = \dfrac{DC}{6.73}
DC = 6.73 \times \sin(42) = 4.50 cm (2 dp)
Question 6:
OL and NL are ladders leaning against a vertical wall OM.
NM is 12 cm long
LM is 6.5 cm
Angle OLM is 49.5 \degree.
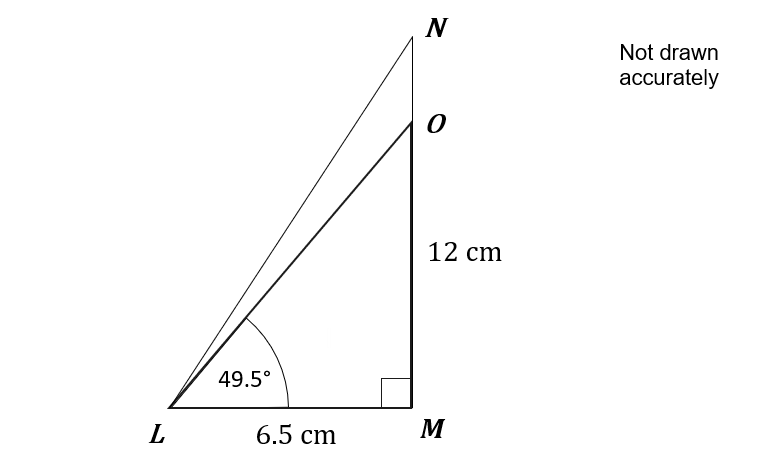
Question 6(a): [3 marks]
Find the length of the line ON.
Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 4.39 cm
WORKING:
\tan (49.5) = \dfrac{MO}{6.5}
MO = \tan (49.5) \times 6.5 = 7.61 cm
NM - MO = NO
12 - 7.61 = 4.39 cm (2 dp)
Question 6(b): [3 marks]
Find the size of angle OLN in the diagram.
Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 12.06 \degree
WORKING:
\tan(NLM) = \dfrac{12}{6.5}
NLM = \tan^{-1} \bigg(\dfrac{12}{6.5} \bigg) = 61.56 \degree
\angle OLN = 61.56 - 49.5 = 12.06 \degree (2 dp)
