Question 1:
A is a cubic graph, B is a reciprocal graph, with equations
A: \, y = x^3 - 1
B: \, y = \dfrac{1}{x}
Question 1(a): [1 mark]
For A, find the values of a, b, c, d, e from the table below.

Answer type: Multiple answers type 1
ANSWER: a = -9 ; b = -2 ; c = -1 ; d = 0 ; e = 7
WORKING:
(-2)^3 - 1 = -9
(-1)^3 - 1 = -2
(0)^3 - 1 = -1
(1)^3 - 1 = 0
(2)^3 - 1 = 7
Question 1(b): [1 mark]
For B, find the values of a, b, c, d, e, f from the table below.

Answer type: Multiple answers type 1
ANSWER: a = -0.5 ; b = -1 ; c = -2 ; d = -4 ; e = 4 ; f = 2
WORKING:
\dfrac{1}{-2} = -0.5
\dfrac{1}{-1} = -1
\dfrac{1}{-0.5} = -2
\dfrac{1}{-0.25} = -4
\dfrac{1}{0.25} = 4
\dfrac{1}{0.5} = 2
Question 1(c): [1 mark]
Choose the correct statement below about the graph drawings.
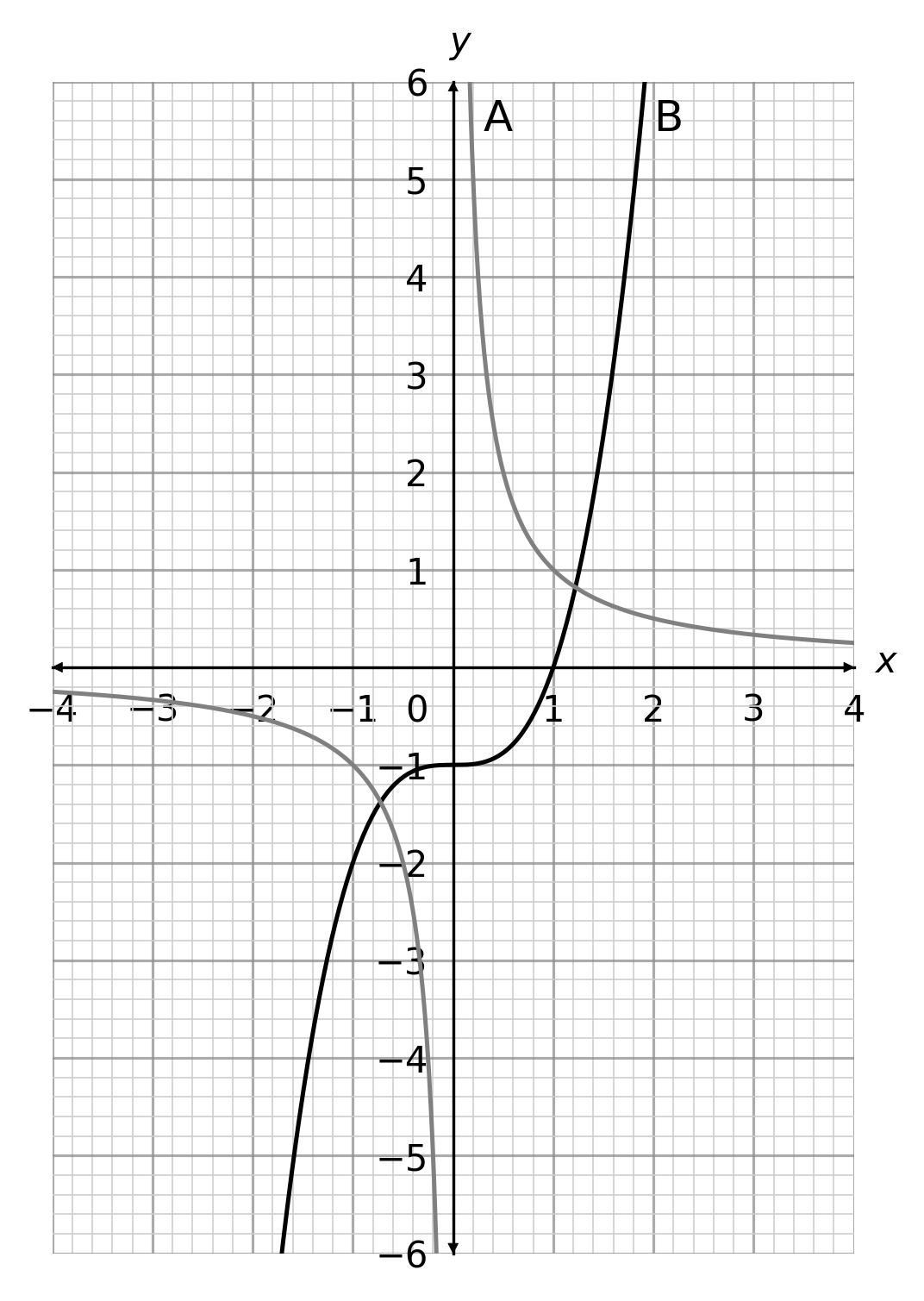
Answer type: Multiple choice type 1
A: A is drawn correctly but B is drawn incorrectly.
B: B is drawn correctly but A is drawn incorrectly.
C: Both A and B are drawn correctly.
D: Both A and B are drawn incorrectly.
ANSWER: C: Both A and B are drawn correctly.
Question 1(d): [2 marks]
What are the approximate points of intersection of the two graphs?
Answer type: Multiple choice type 2
A: (-0.75, -1.4) and (1.2, 0.8)
B: (-0.5, -1.4) and (1.2, 0.8)
C: (-0.75, -1.4) and (0.8,1.2)
D: (-1.4, -0.75) and (1.2, 0.8)
ANSWER: A: (-0.75, -1.4) and (1.2, 0.8)
Question 2(a): [1 mark]
For y = 2^x, find the values of a, b, c, d, e, f from the table.

Answer type: Multiple answers type 1
ANSWER:
0.25
0.5
1
2
4
8
WORKING:
2^{-2} = 0.25
2^{-1} = 0.5
2^{0} = 1
2^{1} = 2
2^{2} = 4
2^{3} = 8
Question 2(b): [1 mark]
What is the correct graph for y = 2^x?
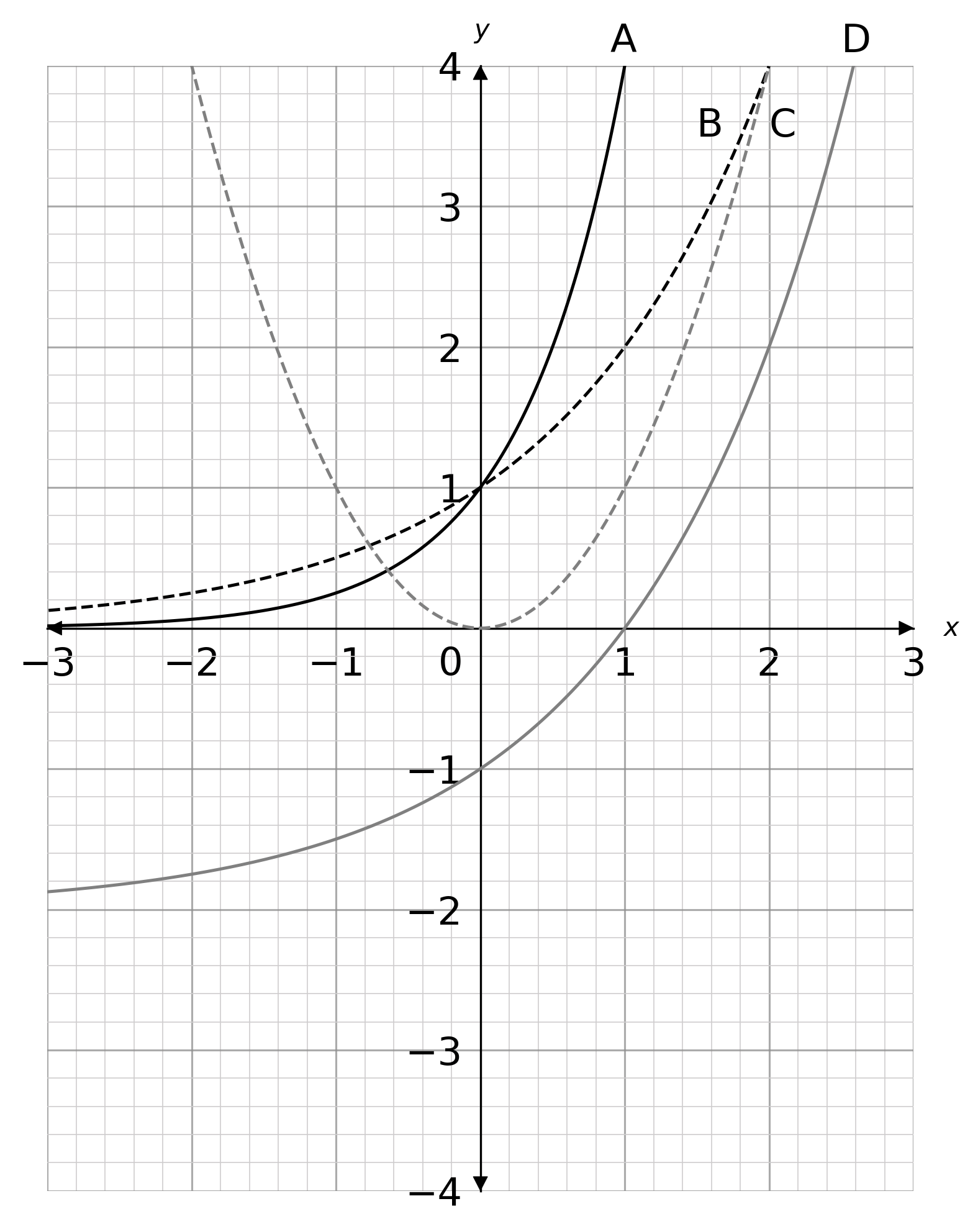
Answer type: Multiple choice type 1
A: A
B: B
C: C
D: D
ANSWER: B: B
Question 3: [2 marks]
The grid below shows the graph of N = Ar^t, which represents the number of bacteria in a sample (N) over a period of time (t). A and r are constants.
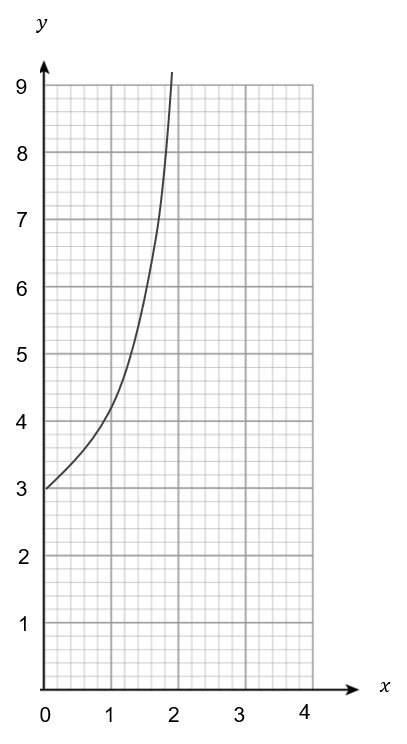
Use the graph to find the values of the constants A and r.
Choose the correct answer.
Answer type: Multiple choice type 1
A: A = 2, \, r = 3
B: A = 3, \, r = 2
C: A = 4, \, r = 6
D: A = 6, \, r = 4
ANSWER: B: A = 3, \, r = 2
WORKING:
Instead of x and y, it is t and N respectively.
Two coordinates that can easily be chosen are (0,3) and (1,6).
Substituting first to set of coordinates to find A:
N = Ar^t
3 = A \times r^0
3 = A \times 1
A = 3
N = 3r^t
Substituting the second set of coordinates to find r:
N = 3r^t
6 = 3r^1
6 = 3r
r = 2
So A = 3, r = 2.
Question 4: [6 marks]
There are 6 equations as follows:
A: y = \dfrac{1}{x}
B: y = - \dfrac{1}{x}
C: y = \dfrac{1}{10x}
D: y = e^x
E: y = 0.5 x
F: y = - e^x
and 6 graphs:
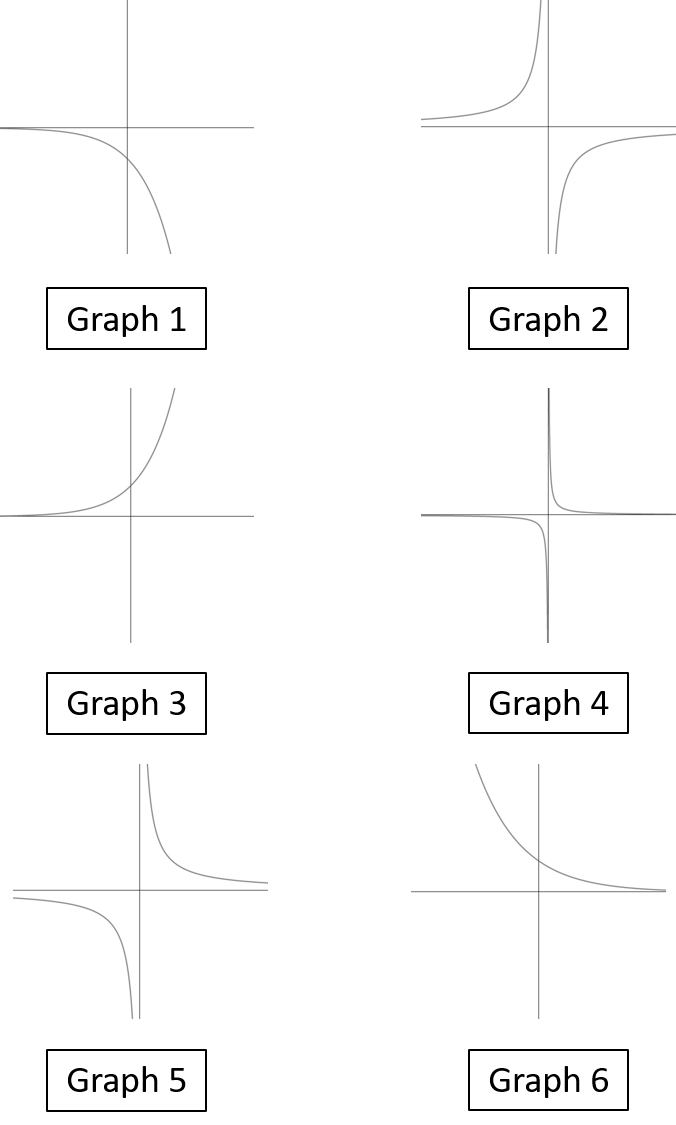
Match the graphs to the equations.
Answer type: Multiple answers type 1
ANSWER:
Graph 1 = F
Graph 2 = B
Graph 3 = D
Graph 4 = C
Graph 5 = A
Graph 6 = E
Question 5(a): [1 mark]
y=\dfrac{3}{x} is the equation for a reciprocal graph.
For the equation y=\dfrac{3}{x}, find the values of a, b, c, d, e, f shown in the table below.

Answer type: Multiple answers type 1
ANSWER:
a = -1
b = -1.5
c = -3
d = 3
e = 1.5
f = 1
WORKING:
\dfrac{3}{-3} = -1
\dfrac{3}{-2} = -1.5
\dfrac{3}{-1} = -3
\dfrac{3}{1} = 3
\dfrac{3}{2} = 1.5
\dfrac{3}{3} = 1
Question 5(b): [2 marks]
What is the correct graph for y= \dfrac{3}{x}?
Answer type: Multiple choice type 1
A: 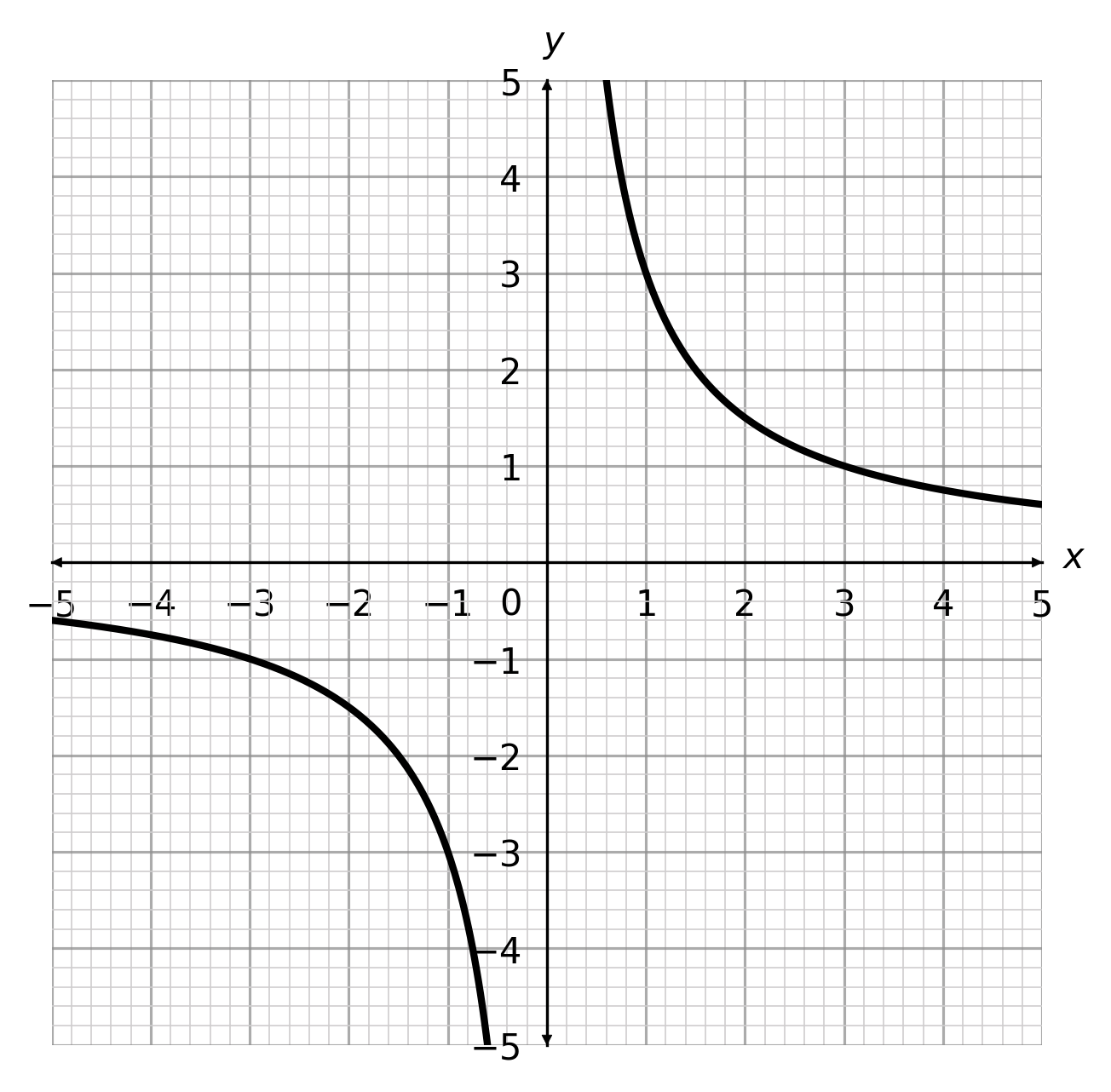 B:
B:  C:
C: 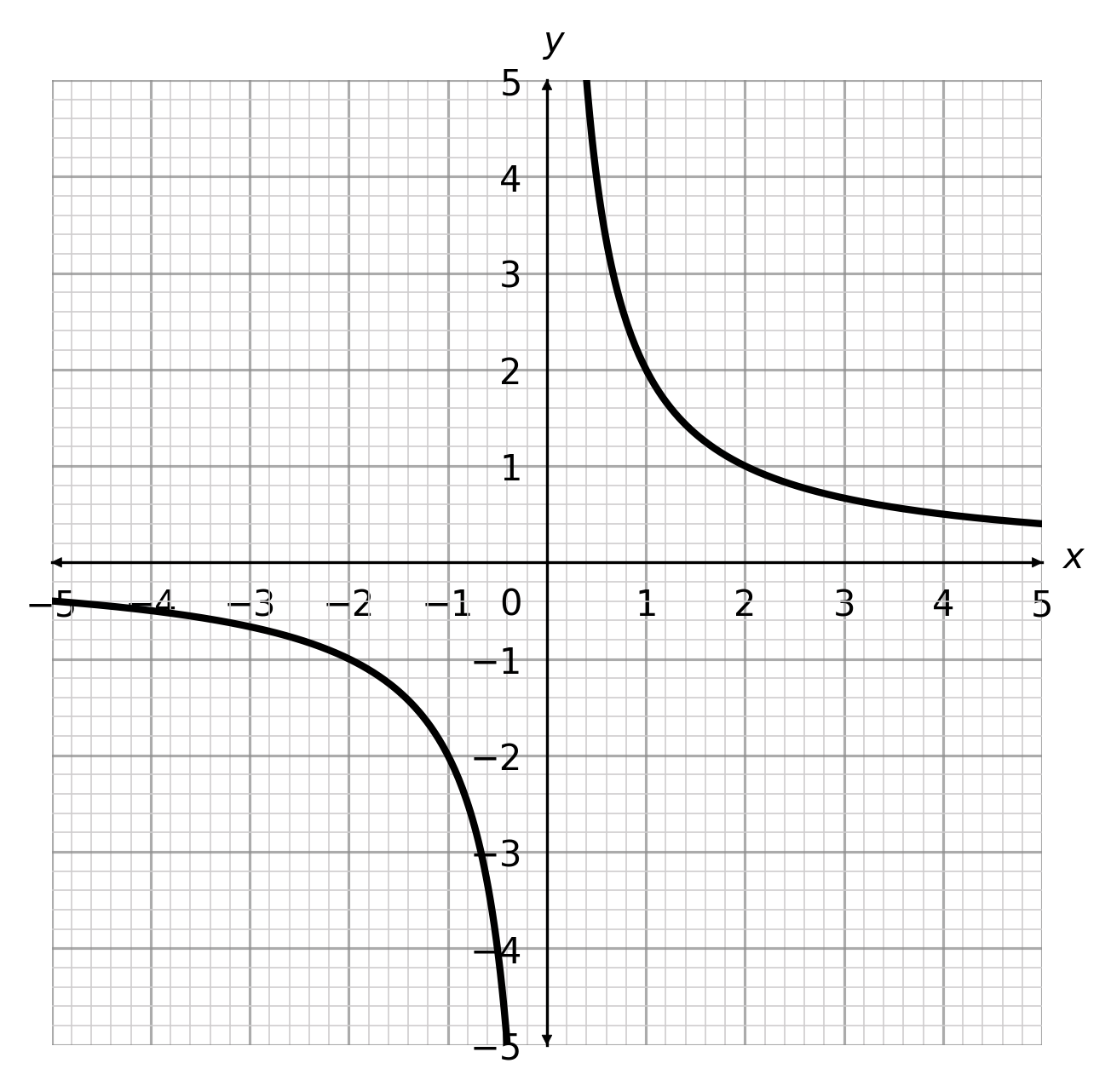 D:
D: 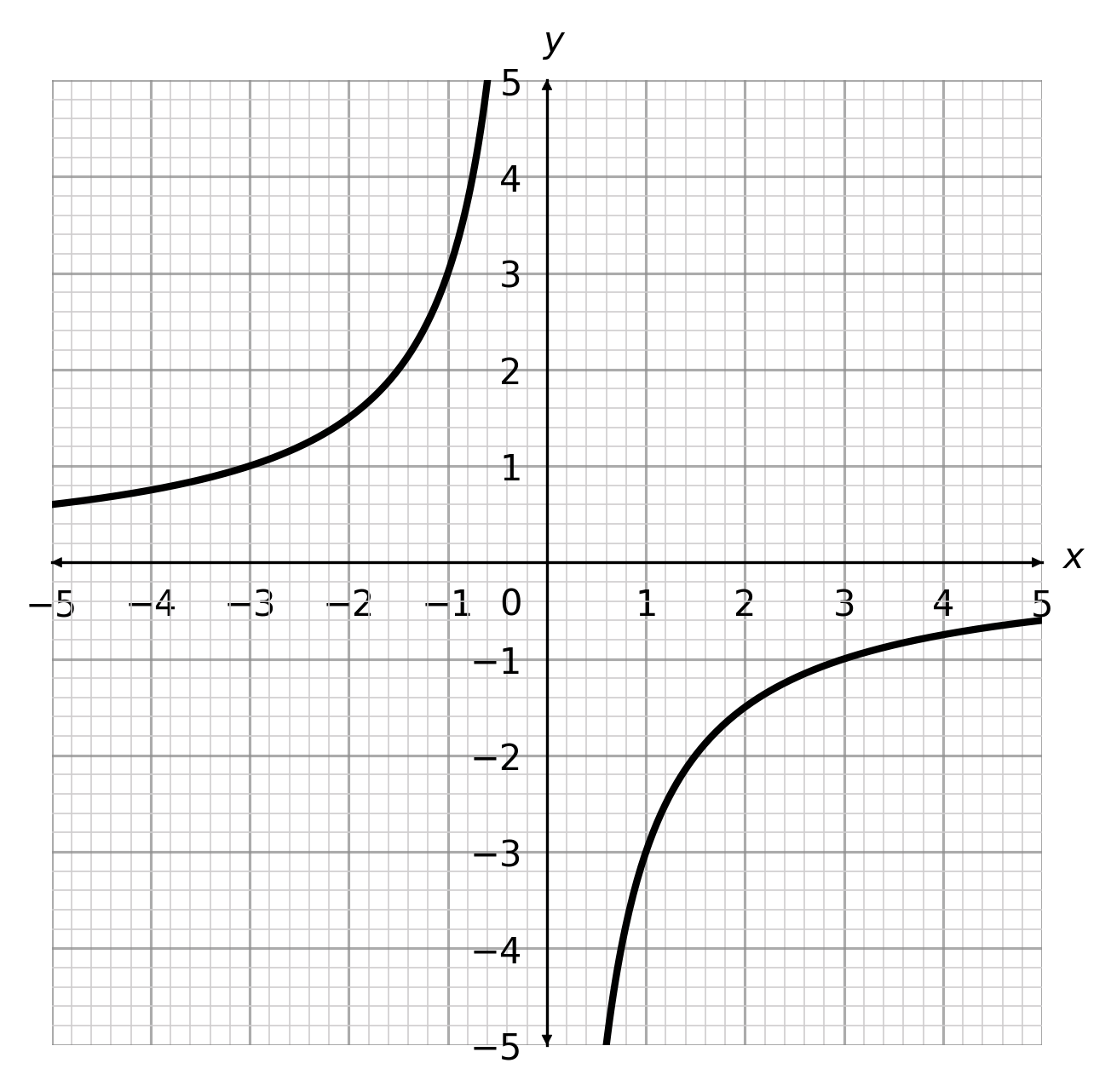
ANSWER: A
Question 6(a): [1 mark]
y=(\frac{1}{4})^x is the equation for a exponential graph.
For y=(\frac{1}{4})^x, find the values of a, b, c, d, e from the table.
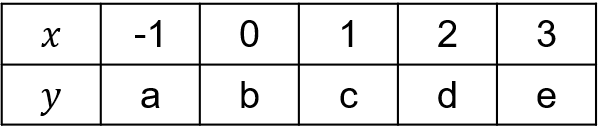
Answer type: Multiple answers type 1
ANSWER:
a = 4
b = 1
c = 0.25
d = 0.0625
e = 0.015625
WORKING:
(\frac{1}{4})^{-1} = 4
(\frac{1}{4})^{0} = 1
(\frac{1}{4})^{1} = 0.25
(\frac{1}{4})^{2} = 0.0625
(\frac{1}{4})^{3} = 0.015625
Question 6(b): [2 marks]
What is the correct graph for y = (\frac{1}{4})^x?
Answer type: Multiple choice type 1
A: 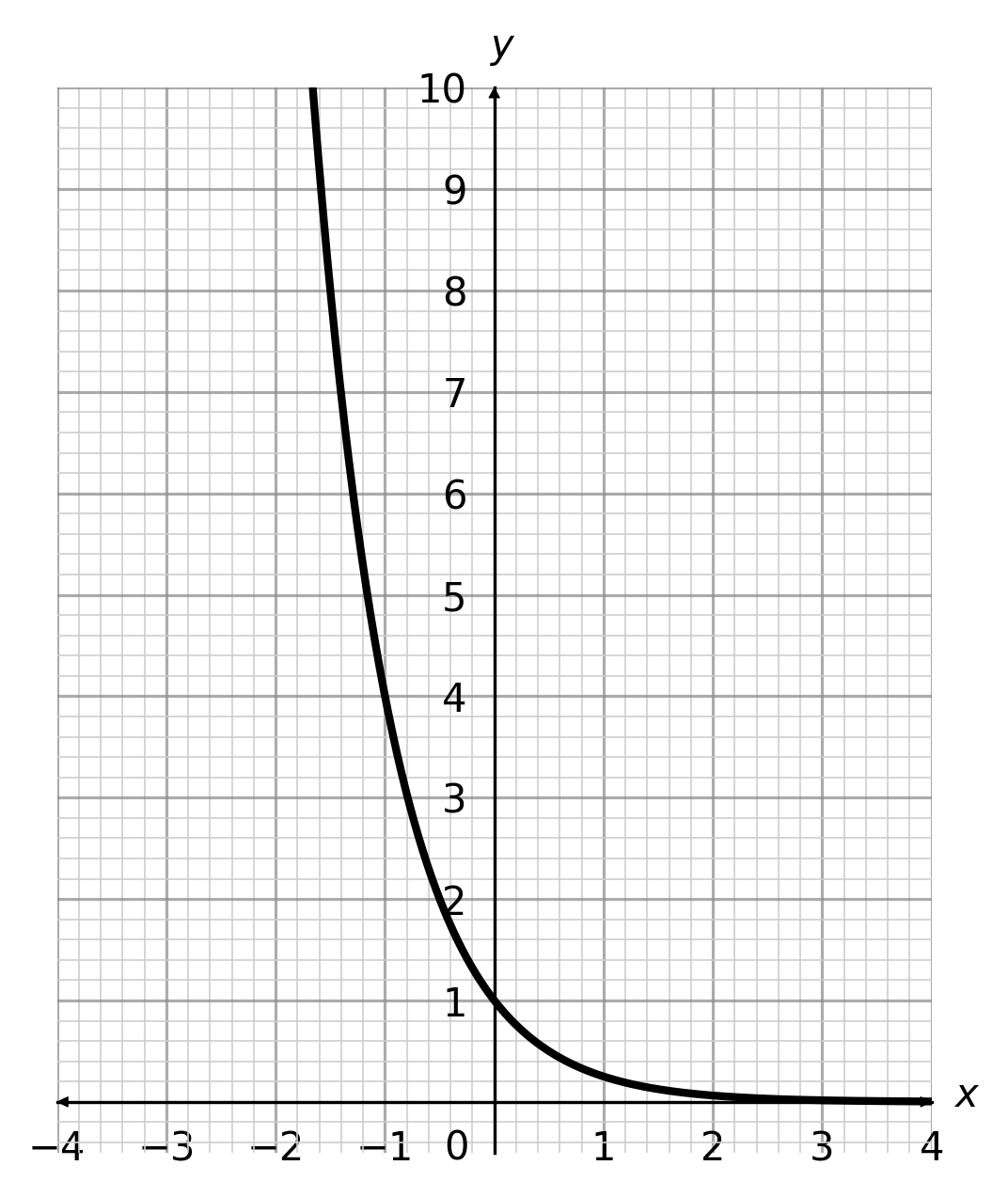 B:
B: 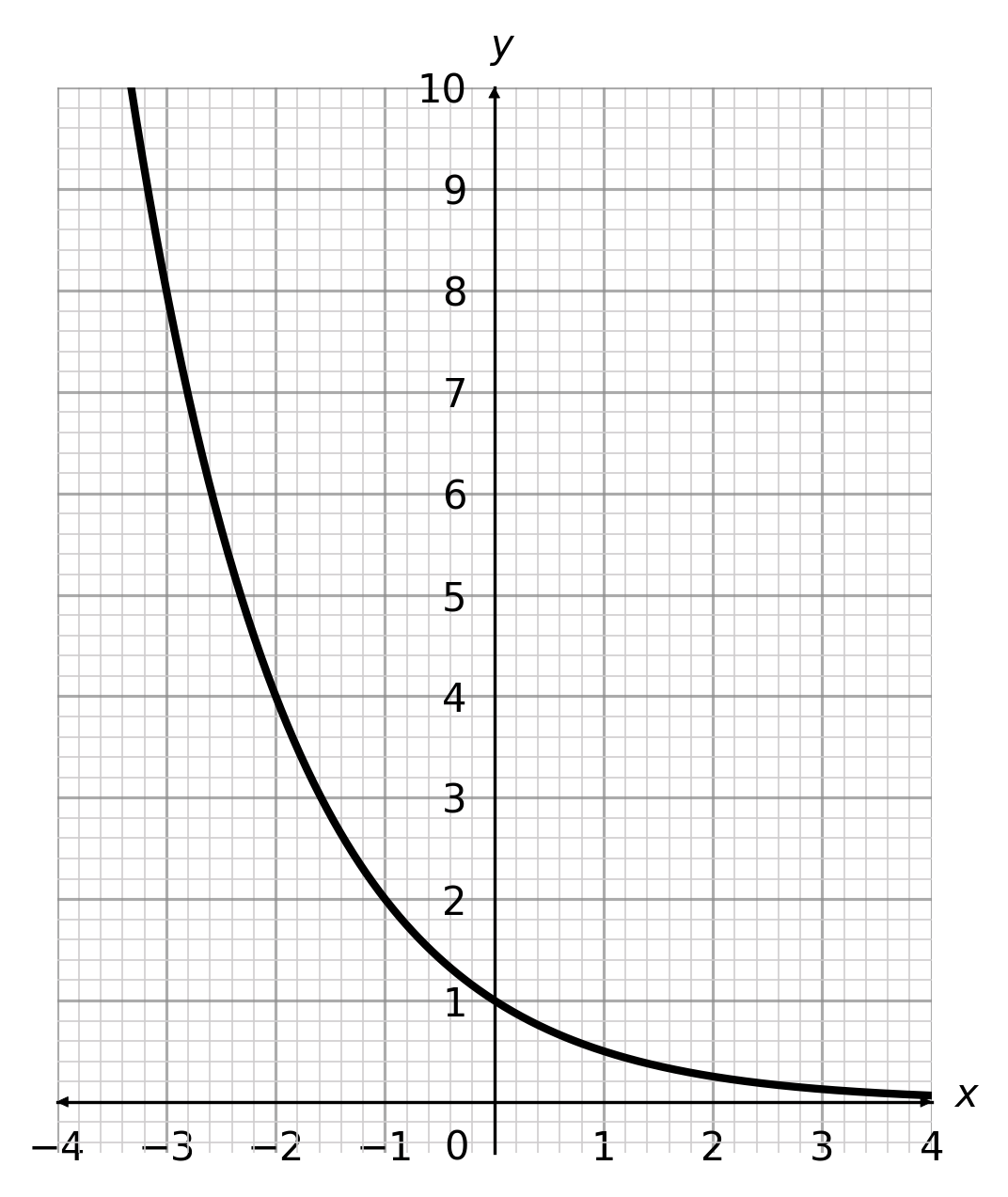 C:
C: 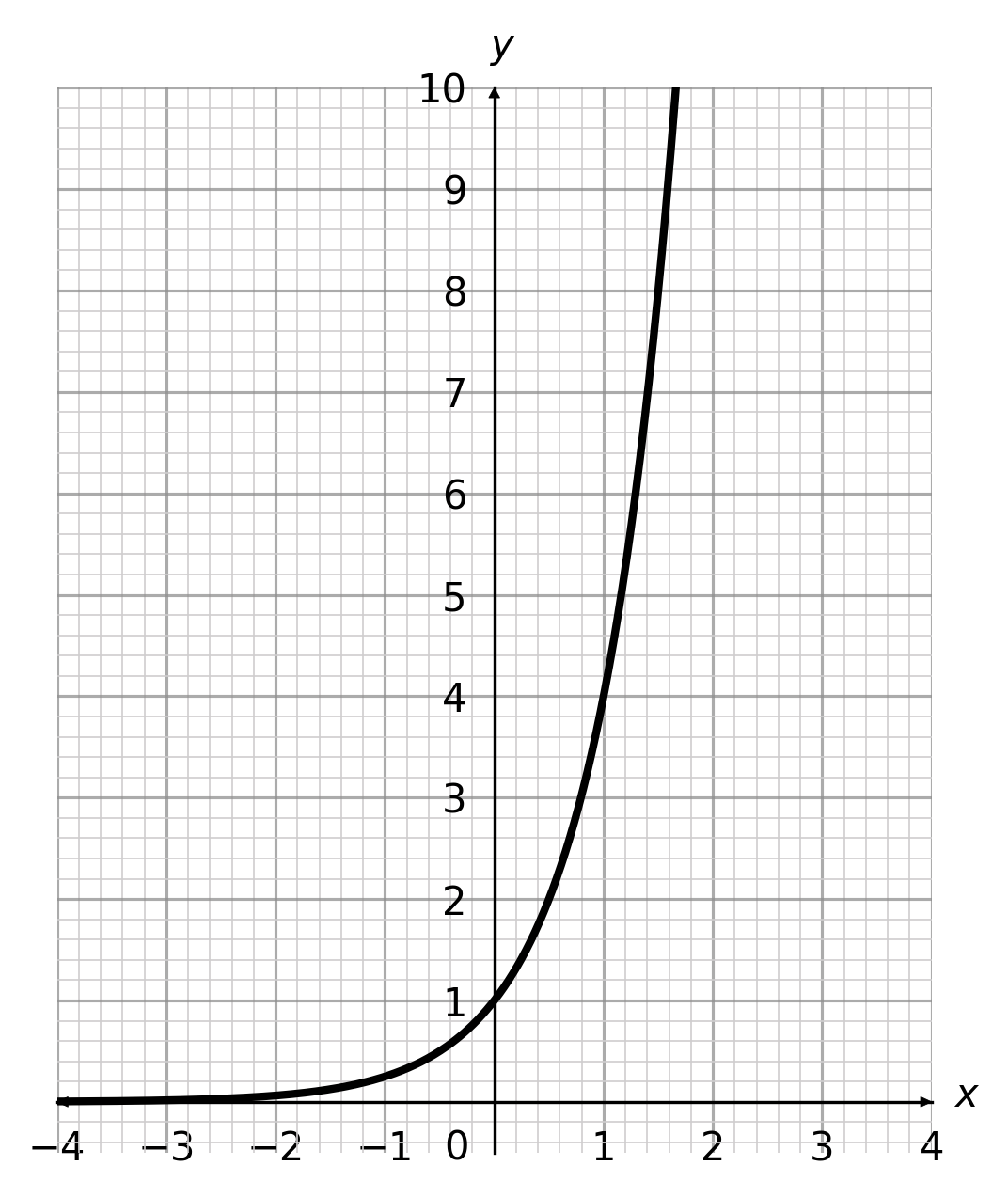 D:
D: 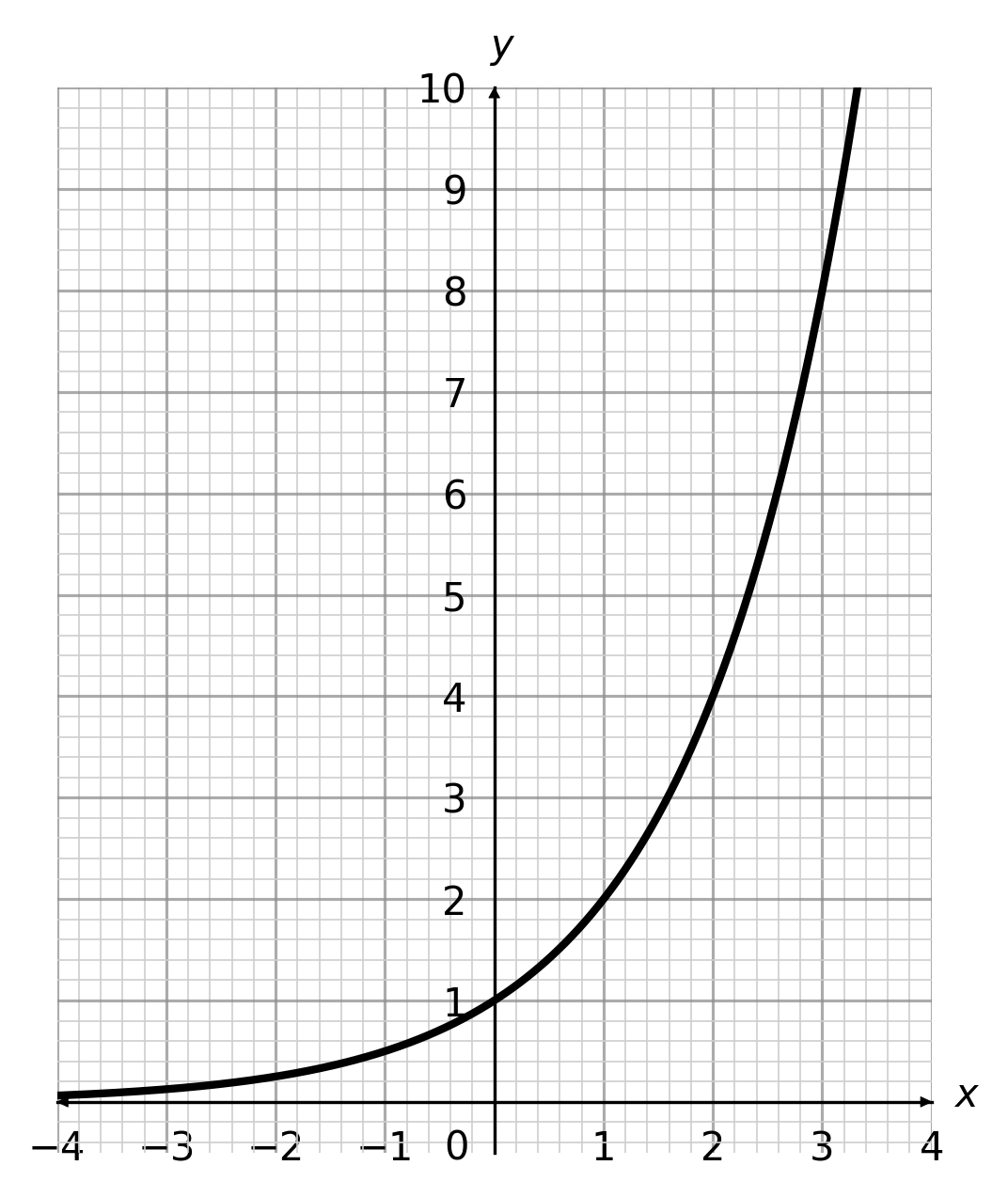
ANSWER: A
