Question 1
LEVEL 6
A graph has the following equation: xy = 26
Without any calculation, what type of graph is it?
Select the correct statement from the list below.
A: It is a reciprocal graph
B: It is an exponential graph
C: It is neither a reciprocal graph nor an exponential graph
D: I would need plot the graph to be able to tell
CORRECT ANSWER: A
WORKED SOLUTION:
Any reciprocal graph has the form xy = a or equivalently y = \frac{a}{x}
Question 2
LEVEL 6
A graph has the following equation: y = (5)^x
Without any calculation, what type of graph is it?
Select the correct statement from the list below.
A: It is an exponential graph
B: It is a reciprocal graph
C: It is neither a reciprocal graph nor an exponential graph
D: I would need plot the graph to be able to tell
CORRECT ANSWER: A
WORKED SOLUTION:
Any exponential graph has the form y=k^x
The graph here can also be written as y = 5^{x}
Question 3
LEVEL 6
What is the correct plot for the equation y = \frac{4}{x}?
A: 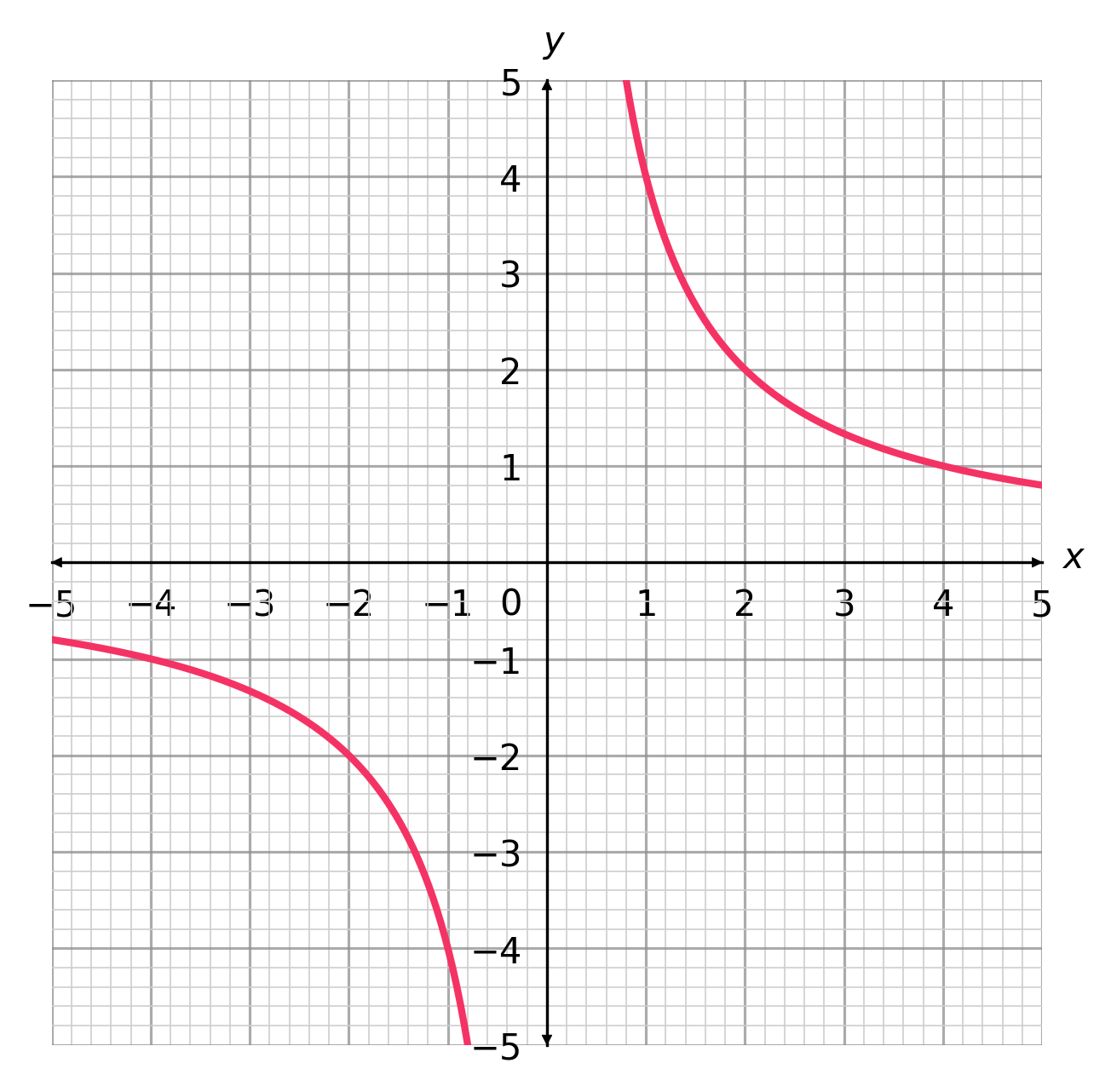 B:
B: 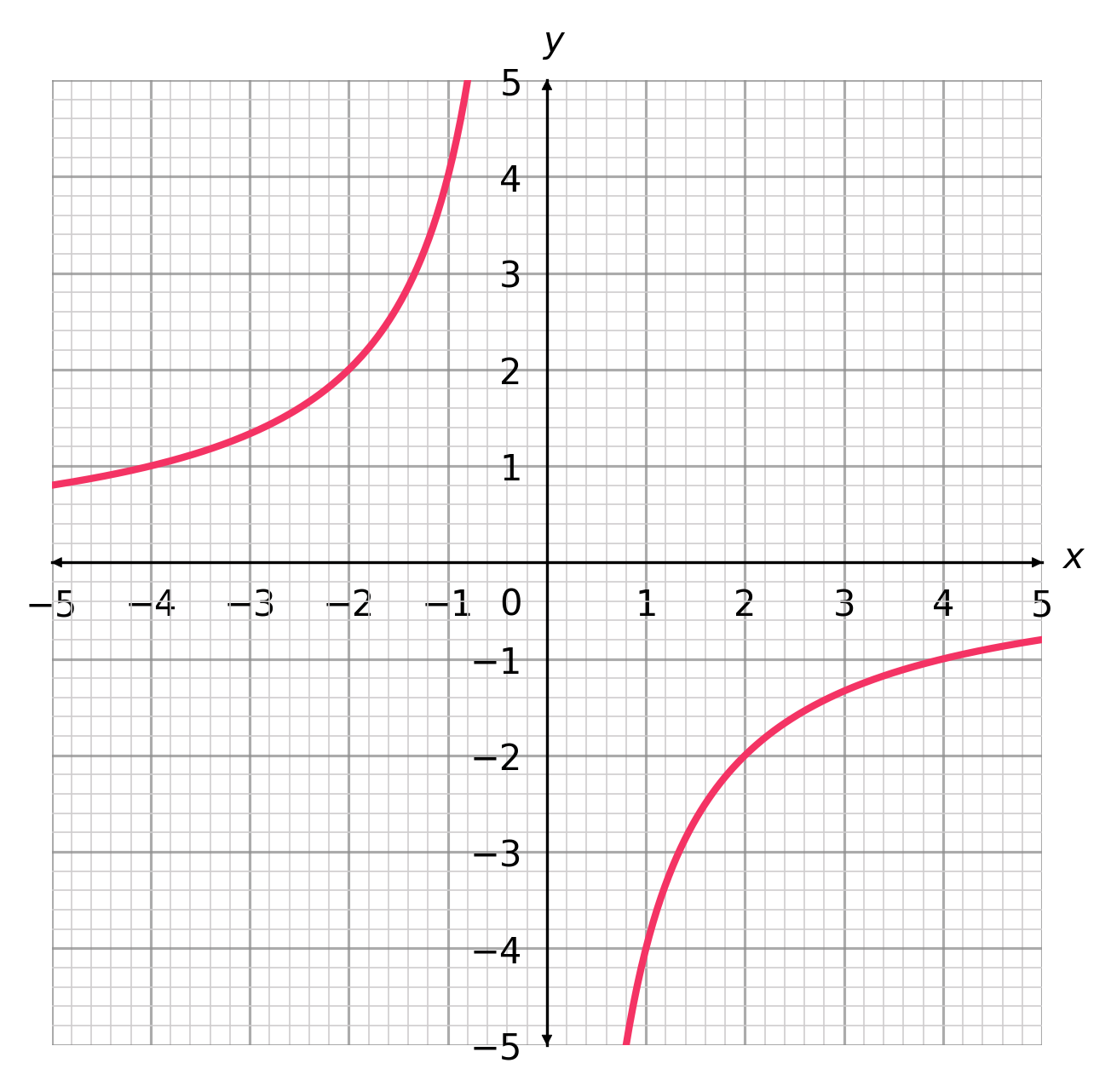 C:
C: 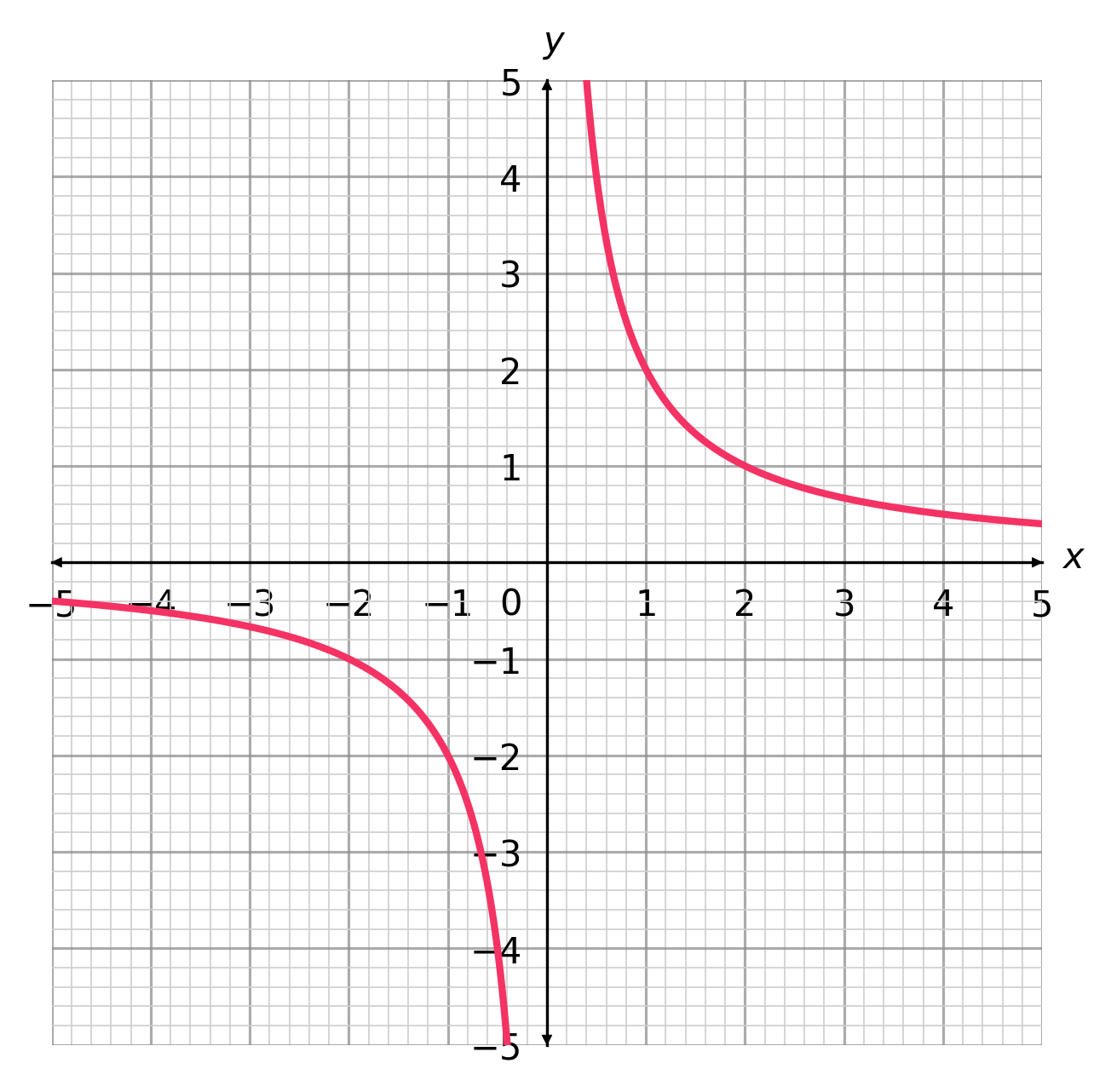 D:
D: 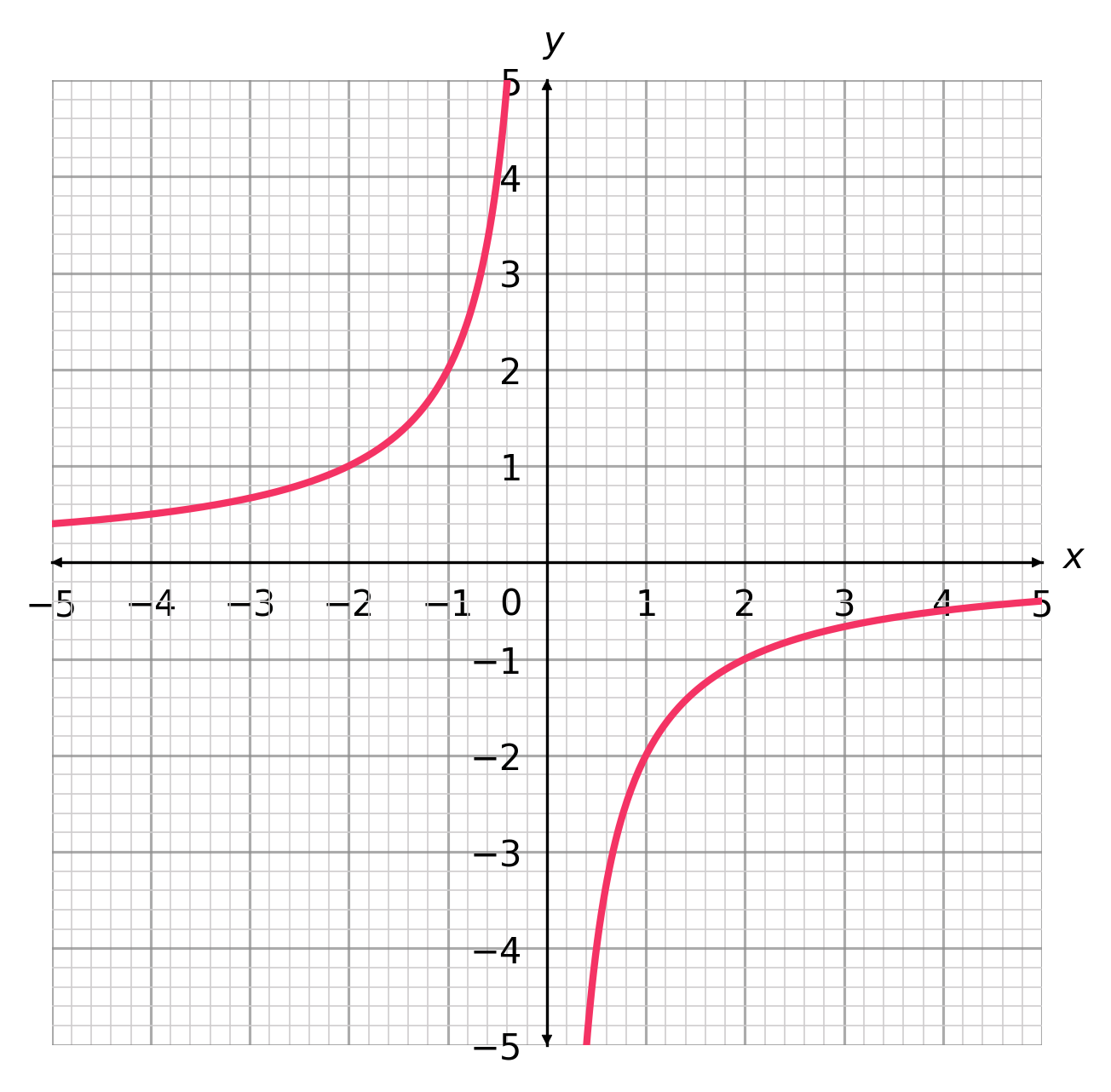
CORRECT ANSWER: A
WORKED SOLUTION:
To identify the correct plot, we know that the graph should by symmetrical about the line y=-x.
Since y=\frac{4}{x}, we know that the graph must pass through the points (4,1) and (1,4), and since it is symmetrical about y=-x, it must pass through the points (-1,-4) and (-4,-1) also.
Therefore we get the following graph

Question 4
LEVEL 6
What is the correct plot for the equation y = 2^x, between x=-3 and x=3?
A: 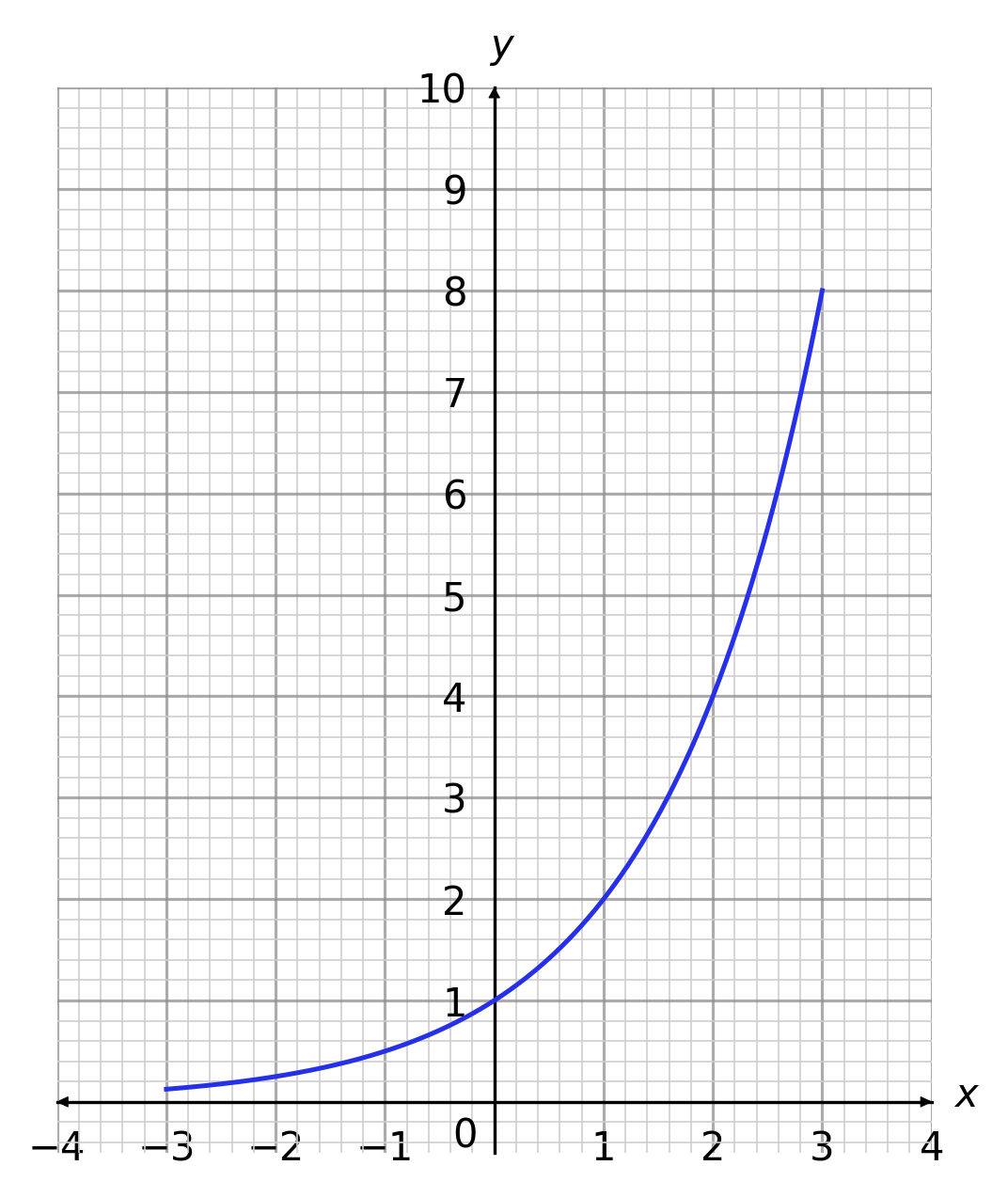 B:
B: 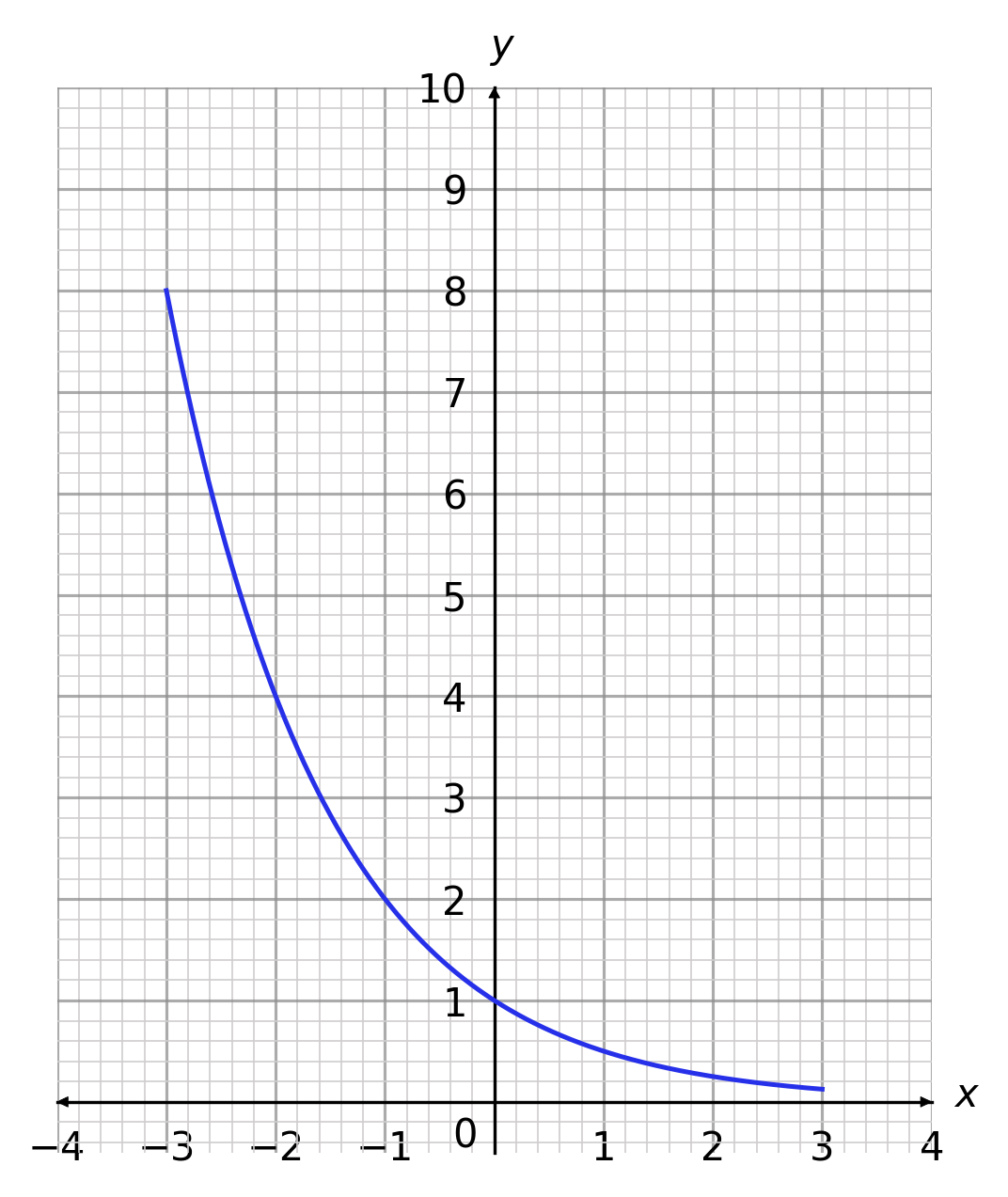 C:
C: 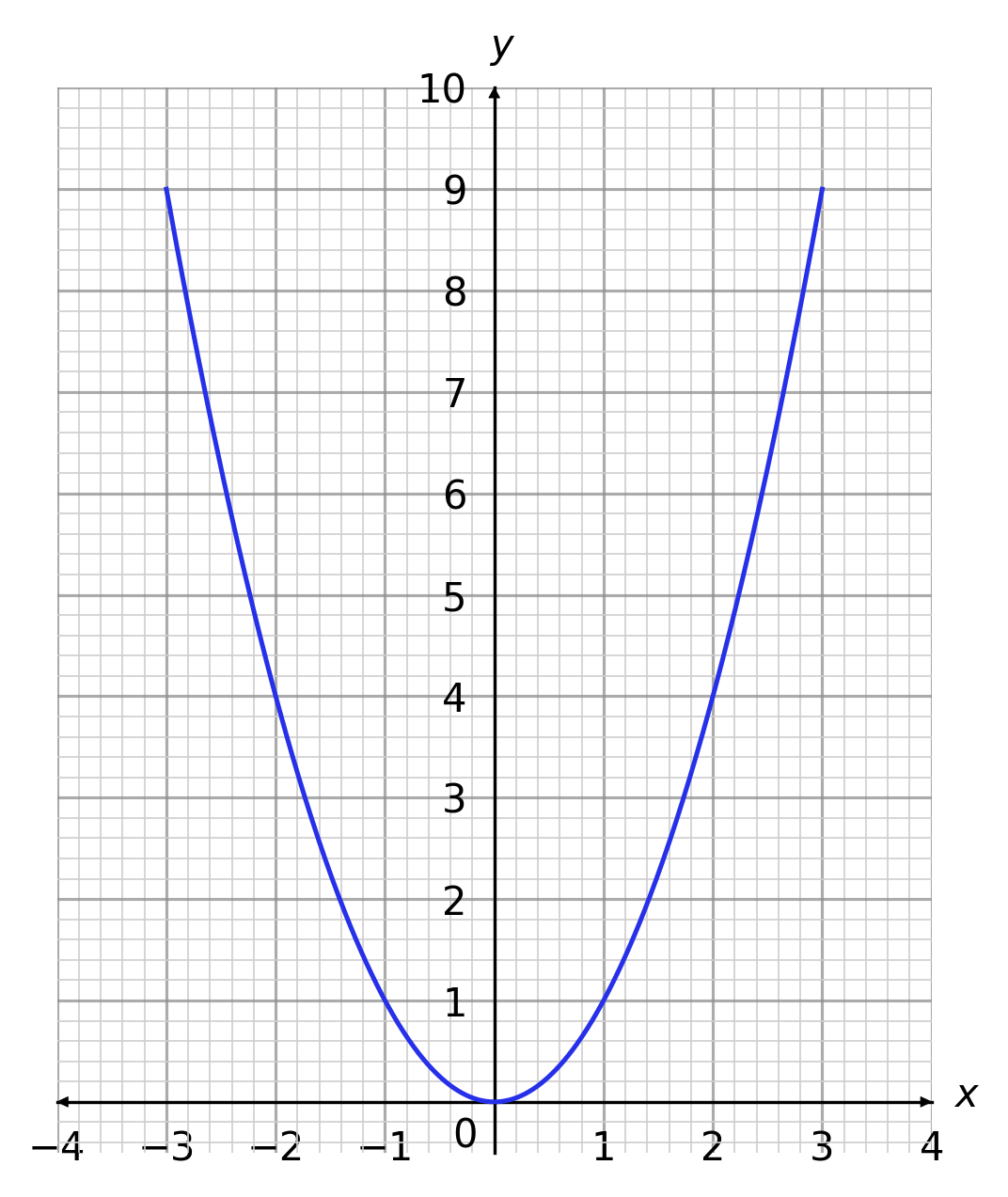 D:
D: 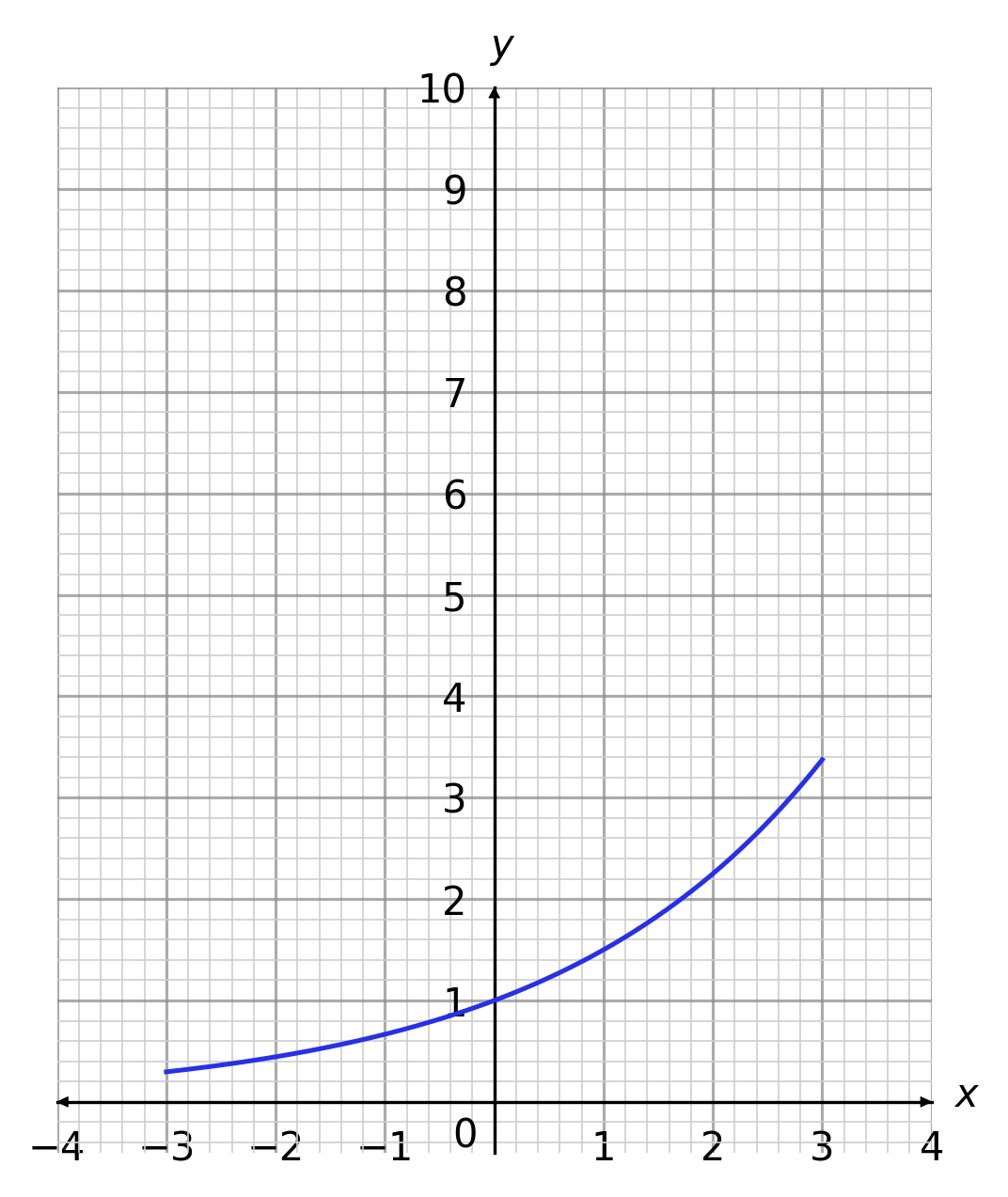
CORRECT ANSWER: A
WORKED SOLUTION:
We need to substitute various x values into our equation to find the corresponding y values.
\text{When }x=-3 \hspace{1cm}\rightarrow \hspace{1cm}y=2^{-3}=0.125
\text{When }x=-2 \hspace{1cm}\rightarrow \hspace{1cm}y=2^{-2}=0.25
\text{When }x=-1 \hspace{1cm}\rightarrow \hspace{1cm}y=2^{-1}=0.5
\text{When }x=0 \hspace{1cm}\rightarrow \hspace{1cm}y=2^{0}=1
\text{When }x=1 \hspace{1cm}\rightarrow \hspace{1cm}y=2^{1}=2
\text{When }x=2 \hspace{1cm}\rightarrow \hspace{1cm}y=2^{2}=4
\text{When }x=3 \hspace{1cm}\rightarrow \hspace{1cm}y=2^{3}=8
Plot these coordinates
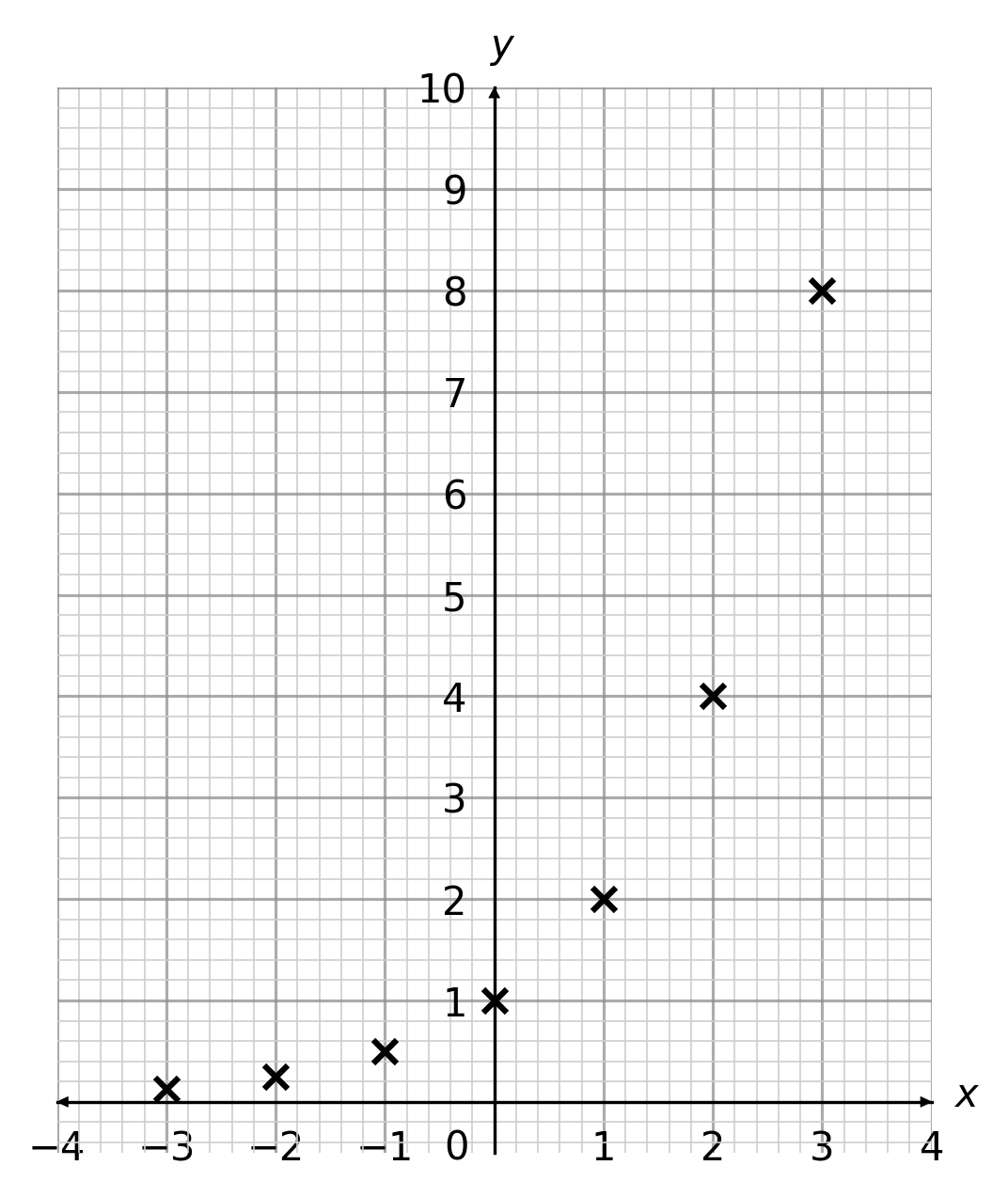
Then join these up to plot the graph
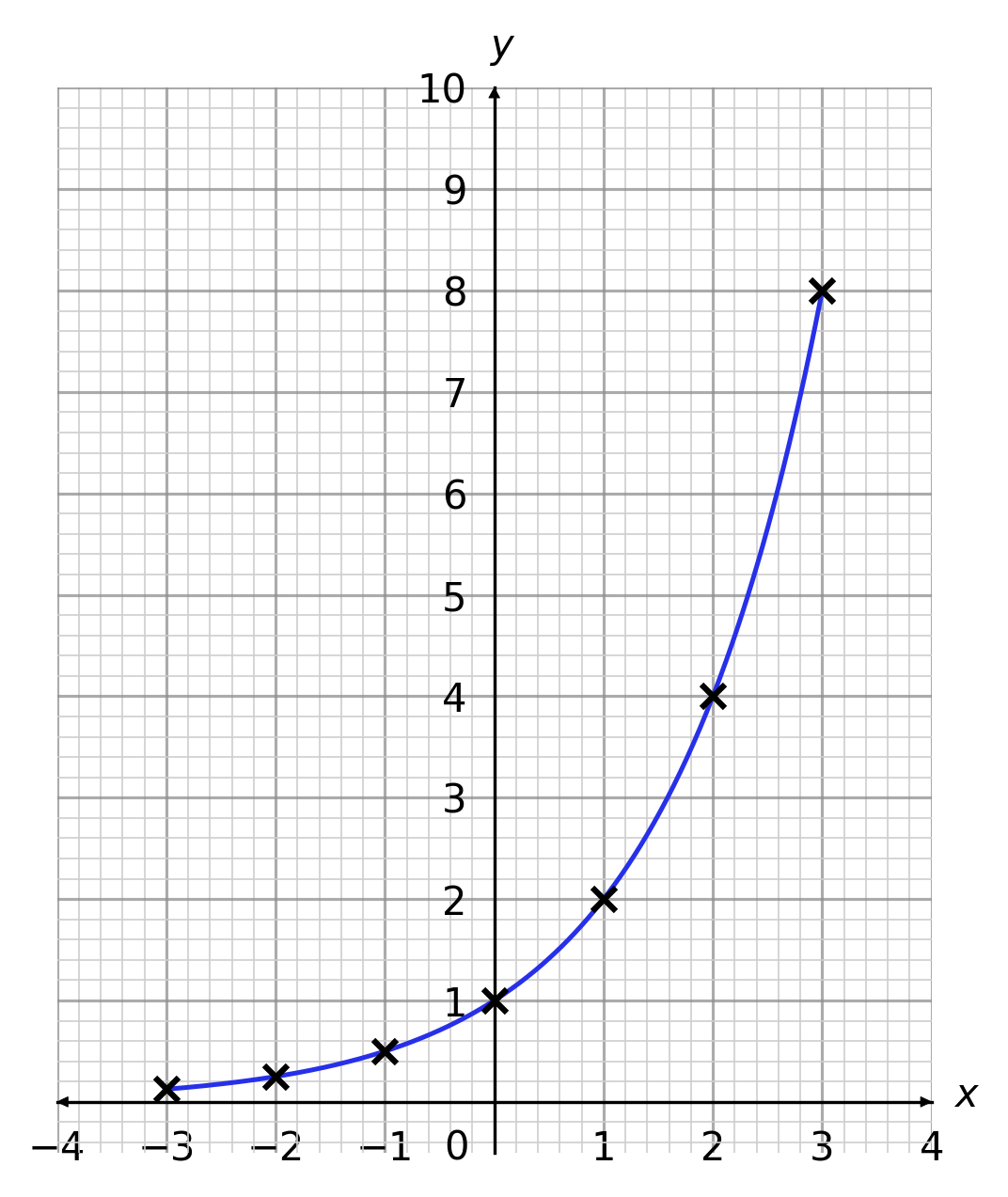
Question 5
LEVEL 6
Given that the following plot has equation y=(\frac{1}{3})^x, choose the correct plot for the equation y=3^x?
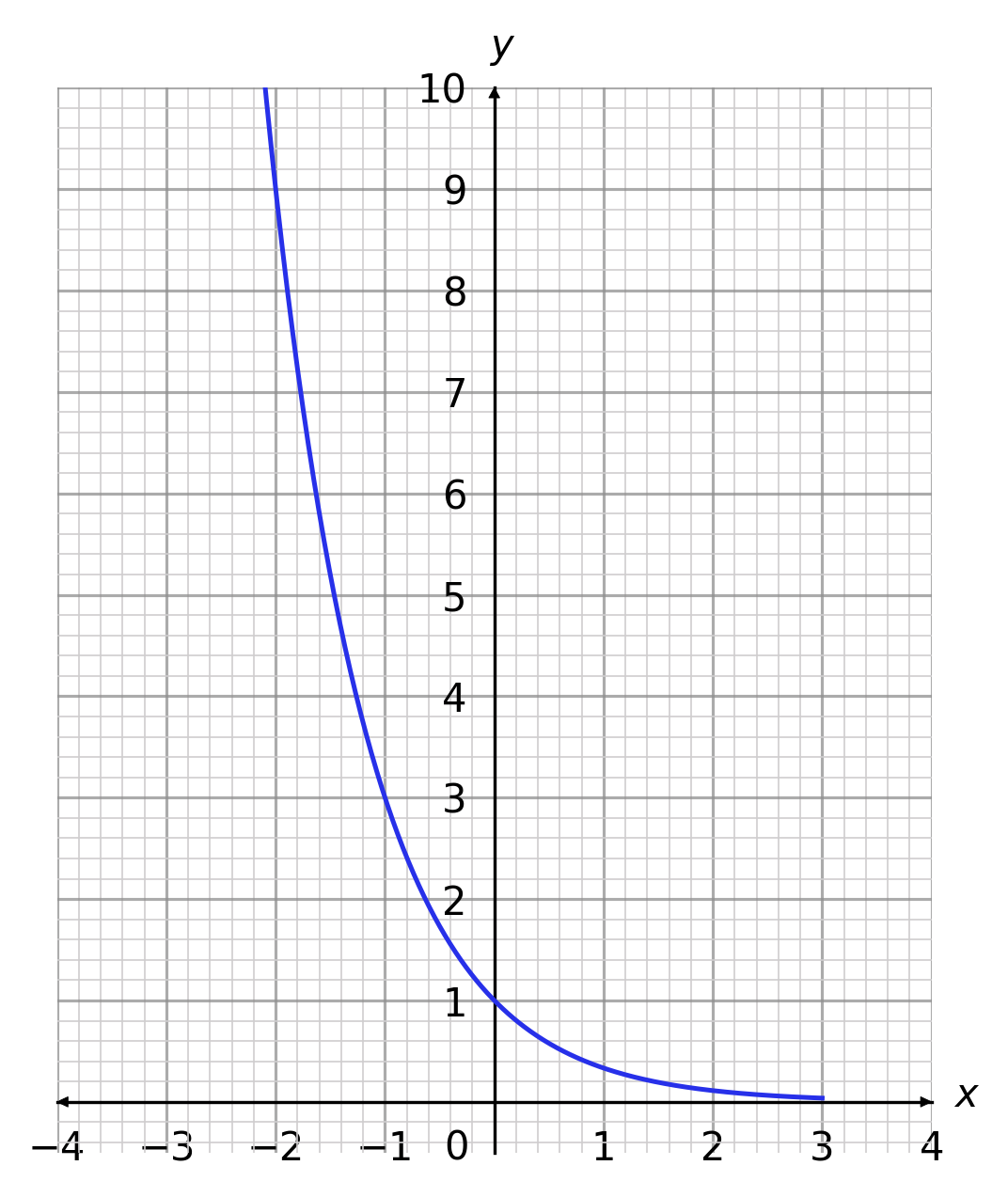
A: 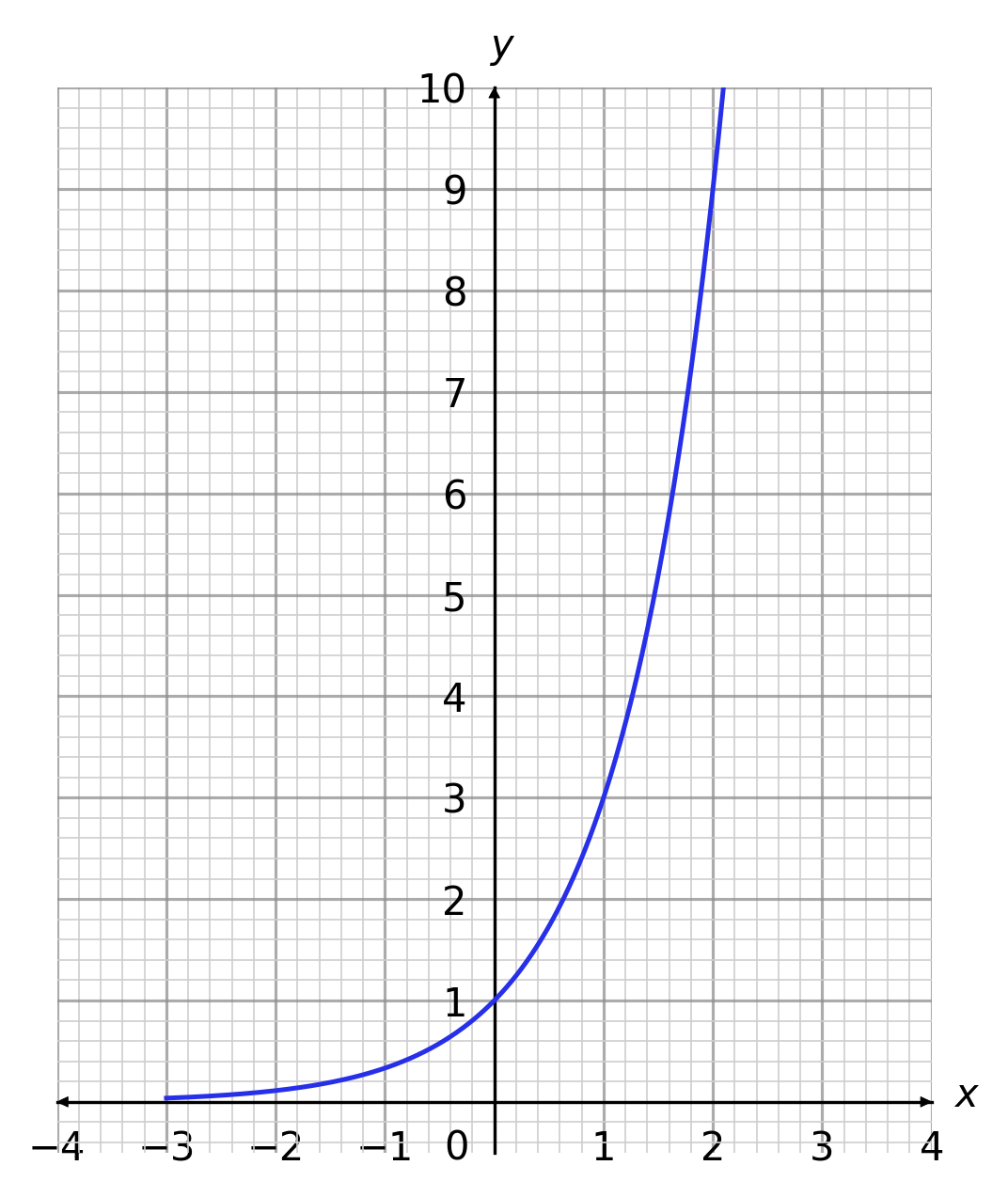 B:
B: 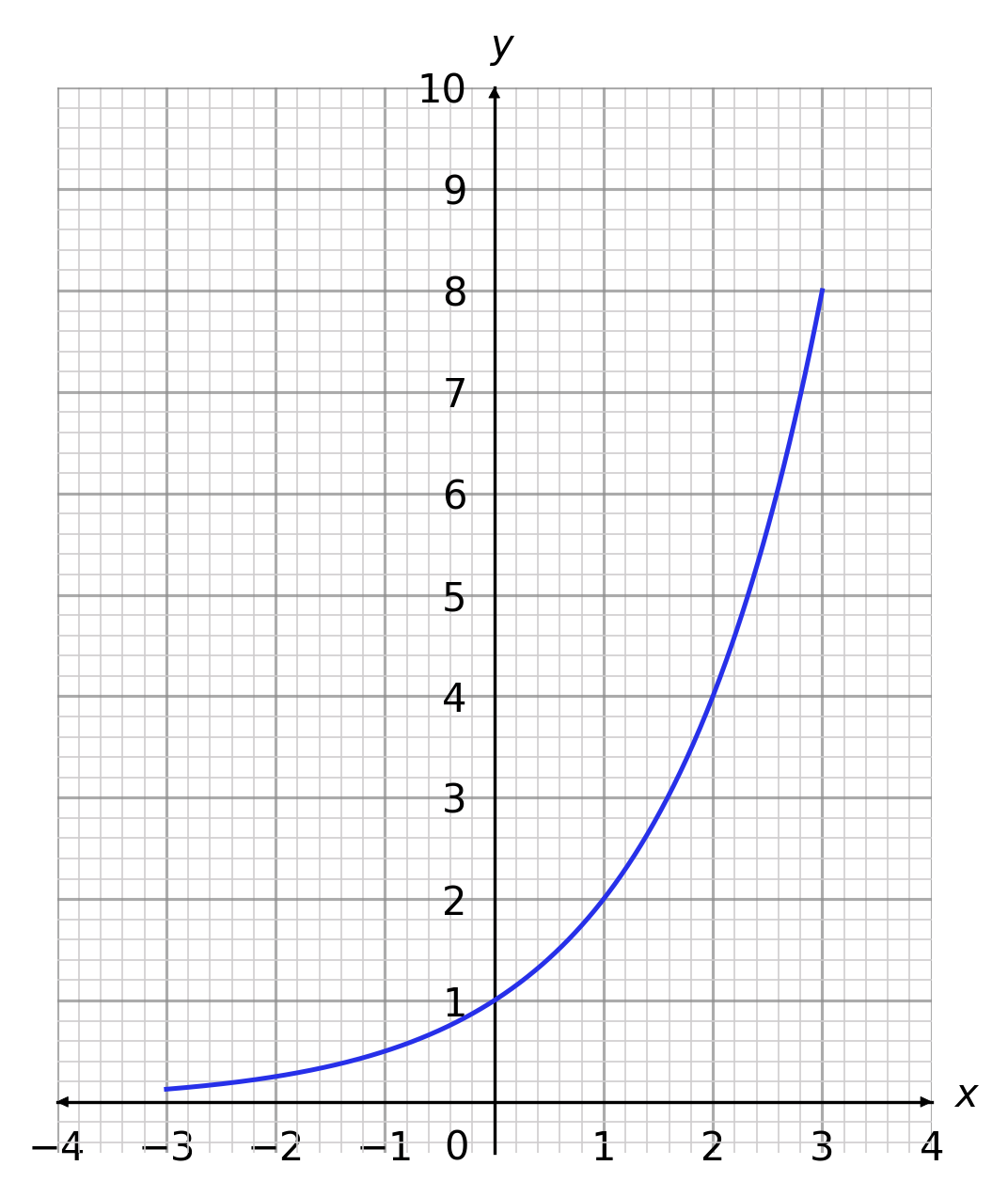 C:
C:  D:
D: 
CORRECT ANSWER: A
WORKED SOLUTION:
y=(\frac{1}{3})^x and y=3^x are symmetrical about the y-axis.
Therefore we flip the graph of y=(\frac{1}{3})^x horizontally to get the following graph.

