11.5 Similar Shapes (level 6+)

Question 1

LEVEL 6

Given that shapes $A$ and $B$ are similar, and that shape $B$ is a scale factor of $3$ times bigger than $A$, work out the area of $B$.

Select the correct answer from the list below:

A: $\dfrac{7}{3}$ cm$^2$

B: $21$ cm$^2$

C: $63$ cm$^2$

D: $147$ cm$^2$

CORRECT ANSWER:    C: $63$ cm$^2$

WORKED SOLUTION:

To find the area of a second shape based on the scale factor, we have to multiply the original area by the square of the scale factor.

$\text{Area of B}=7\times3^2=7\times9=63$ cm$^2$

 

---

 

Question 2

LEVEL 6

The diagram shows two similar shapes, $A$ and $B$.

Shape $A$ has an area of $15$ m$^2$ and shape $B$ has an area of $60$ m$^2$. Shape $A$ has a side length of $3$ cm.

Find the value of $x$ from shape $B$.

 

 

Select the correct answer from the list below:

A: $6$ cm

B: $4$ cm

C: $9$ cm

D: $2$ cm

CORRECT ANSWER:    A: $6$ cm

WORKED SOLUTION:

The scale factor between the areas is $60 \div 15 = 4$

Therefore the scale factor between the side lengths is $\sqrt{4} = 2$

Therefore, $x = 3 \times 2 = 6$ cm

 

---

 

Question 3

LEVEL 6

The diagram shows two similar solids, shape $A$ and shape $B$.

 

 

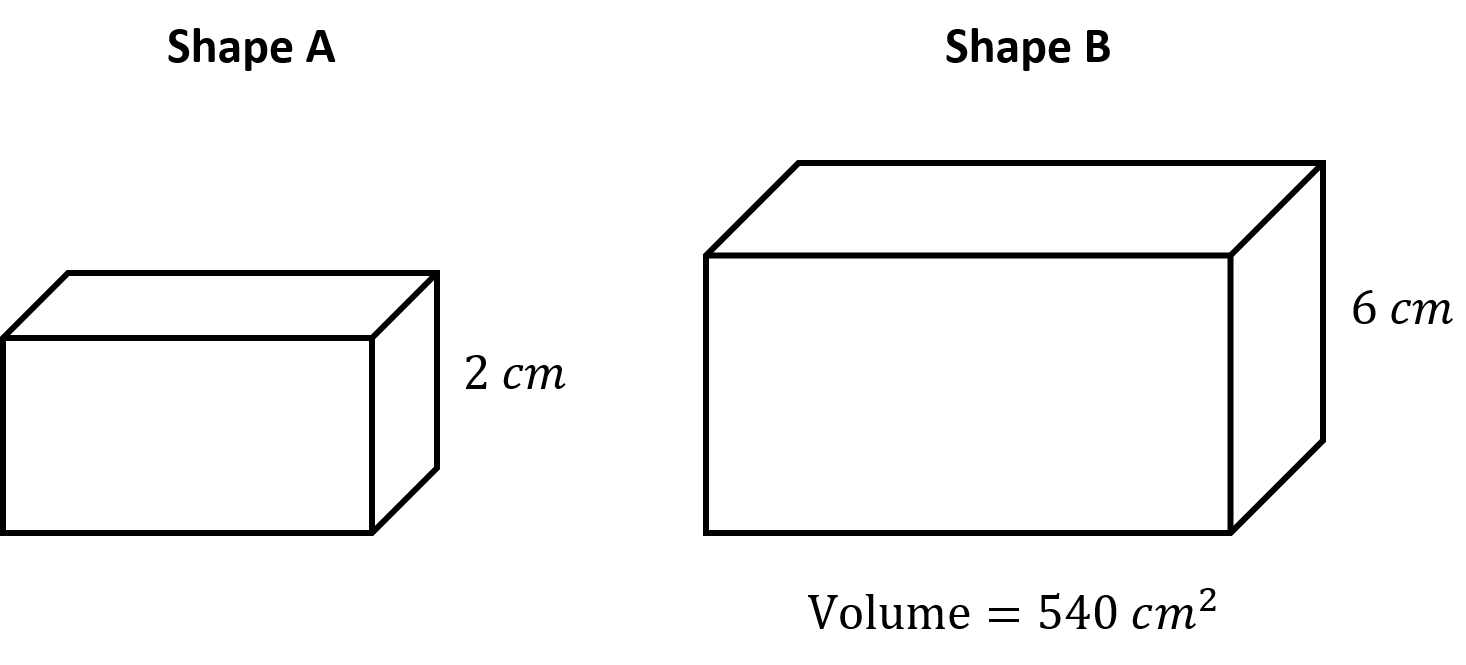
Calculate the volume of shape $A$.

 

Select the correct answer from the list below:

A: $20$ cm$^3$

B: $60$ cm$^3$

C: $270$ cm$^3$

D: $180$ cm$^3$

 

CORRECT ANSWER:    A: $20$ cm$^3$

WORKED SOLUTION:

The scale factor between side lengths is $6 \div 2 = 3$

Therefore the scale factor between volumes is $3^3 = 27$

To find the volume of shape $A$ we need to divide the volume of shape $B$ by this scale factor

We get, Volume of Shape $A = 540 \div 27 = 20$ cm $^3$

 

---

 

Question 4

LEVEL 6

Two spheres are similar shapes. Sphere $A$ has a radius of $4$ cm and Sphere $B$ has a radius of $8$ cm.

Calculate the ratio of the volumes between the two spheres.

 

Select the correct answer from the list below:

A: $1:8$

B: $1:4$

C: $1:2$

D: $1:16$

 

CORRECT ANSWER:    A: $1:8$

WORKED SOLUTION:

The scale factor between lengths is $8 \div 4 = 2$

Therefore the scale factor between volumes is $2^3= 8$

Therefore the ratio between volumes is $1:8$

 

---

 

Question 5

LEVEL 6

Shape $A$ and Shape $B$ are similar shapes. Shape $A$ has an area of $25$ cm$^2$.

Calculate the area of Shape $B$.

 

 

Select the correct answer from the list below:

A: $156.25$ cm$^2$

B: $62.5$ cm$^2$

C: $125$ cm$^2$

D: $60$ cm$^2$

 

CORRECT ANSWER:    A: $156.25$ cm$^2$

WORKED SOLUTION:

The scale factor between lengths is $17.5 \div 7 = 2.5$

Therefore the scale factor between areas is $2.5^2 = 6.25$

To find the area of shape $B$ we need multiply the area of shape $A$ by this scale factor

We get, $25 \times 6.25 = 156.25$ cm$^2$