Note: all new questions.
Circles FSQ1
Consider the following circle with a radius of 5 cm

Circles FS1(a)
Calculate the area of the circle to 1 decimal place.
Use the value of \pi = 3.14
Answer type: simple
Answer: 78.5 cm^2
Workings:
\begin{aligned}\text{area} &=\pi r^2 \\ &= 3.14\times5^2 \\ &= 3.14\times25 \\ &= 78.5 \text{ cm}^2\end{aligned}2 marks
Circles FS1(b)
Calculate the circumference of the circle to 1 decimal place.
Answer type: simple
Answer: 31.4 cm
Workings:
\begin{aligned}\text{circumference} &=2\pi \\ &= 2\times3.14\times5 \\ &= 31.4 \text{ cm}\end{aligned}2 marks
Circles FSQ2
Two rival takeaway restaurants are offering different deals on pizzas.
Restaurant A offers 3 ten inch pizzas for £20
Restaurant B offers 2 twelve inch pizzas for £20

Circles FS2(a)
Calculate the total amount of pizza offered by Restaurant A in square inches.
Give your answer to 1 decimal place.
Use the value of \pi = 3.14
Answer type: simple
Answer: 235.5 inch^2
Workings:
\text{radius} = \text{diameter} \div 2 = 10 \div 2 = 5The area of one pizza may be calculated as follows:
\begin{aligned}\text{area} &=\pi r^2 \\ &= 3.14\times5^2 \\ &= 78.5 \text{ inch}^2\end{aligned}Thus the total amount for 3 pizzas is:
78.5\times 3 = 235.5 \text{ inch}^23 marks
Circles FS2(b)
Calculate the total amount of pizza offered by Restaurant B in square inches.
Give your answer to 2 decimal places.
Use the value of \pi = 3.14
Answer type: simple
Answer: 226.08 inch^2
Workings:
\text{radius} = \text{diameter} \div 2 = 12 \div 2 = 6The area of one pizza may be calculated as follows:
\begin{aligned}\text{area} &=\pi r^2 \\ &= 3.14\times6^2 \\ &= 113.04 \text{ inch}^2\end{aligned}Thus the total amount for 2 pizzas is:
113.04\times 2 = 226.04 \text{ inch}^23 marks
Circles FS2(c)
State which of the two restaurants offers more pizza for £20
Answer type: multiple choice
Answer: Restaurant A
Wrong answer: Restaurant B
Workings:
Restaurant A offers 235.5 square inches of pizza, whilst Restaurant B offers 226.04 square inches of pizza.
Thus, Restaurant A offers slightly more pizza.
1 mark
Circles FSQ3
A building is designed featuring a rectangular wall with a large, circular window.

Using the diagram above, calculate the area of the window to 3 decimal places.
You should use the value of \pi = 3.14
Answer type: simple
Answer: 3.462 m^2
Workings:
The diameter of the circle can be calculated as follows:
Diameter = 2.5-0.2-0.2=2.1 m
Thus, the radius of the window is 2.1 \div 2 = 1.05 m
The area, A=\pi r^2, so
A=3.14\times 1.05^2=3.462 to 3 decimal places
4 marks
Circles FSQ4
Jo lives near a large roundabout which has a radius of 10m

Circles FS4(a)
Calculate the area of the roundabout.
You should use the value of \pi = 3.14
Answer type: simple
Answer: 314 m^2
Workings:
The area, A=\pi r^2, so
A=3.14\times 10^2=3.14\times100=314 m^2
2 marks
Circles FS4(b)
If Jo drives around the roundabout 20 times, how far has she driven?
You should use the value of \pi = 3.14
Answer type: simple
Answer: 1256 m
Workings:
The distance around the roundabout is given by the circumference, C=2\pi r, so
C=2\times3.14\times10=62.8 m
So if she drives around the roundabout 20 times, she has driven
20\times62.8=1256 m
2 marks
Circles FSQ5
An architect designs a building with a large square room and four semi-circular rooms attached.
The plan view of the building is shown in the following diagram.
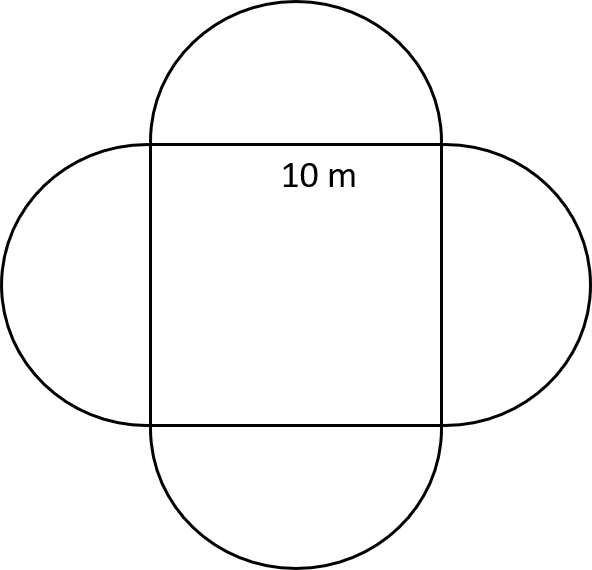
The width of the central square room is 10 m
Calculate the area of the building.
You should use the value of \pi = 3.14
Answer: 257
Workings:
The area of the square room is 10\times10=100 m^2
The remaining rooms are made up of four semi-circles, which is equivalent to two full circles of radius = 5m
Thus, the combined area (A) of these semi-circular rooms is:
A=2\times\pi r^2 = 2\times3.14 \times5^2 = 157 m^2
The total area of the building is therefore:
100+157=257 m^2
4 marks
Circles FSQ6
A garden features a circular fountain with a statue in the middle.
The statue is situated on top of a circular base which takes up a small area at the centre of the fountain.

The fountain has a diameter of 6 m
The base of the statue has a diameter of 1 m
Circles FS6(a)
Calculate the circumference of the fountain to 2 decimal places.
You should use the value of \pi = 3.14
Answer type: simple
Answer: 18.84 m
Workings:
Circumference, C=\pi d, so
C=3.14\times6=18.84 m
1 mark
Circles FS6(b)
Calculate the area of the fountain which is covered by water only.
Give your answer to 1 decimal place.
You should use the value of \pi = 3.14
Answer type: simple
Answer: 109.9 m^2
Workings:
The area covered by water only is the total area of the fountain minus the area covered by the statue base.
The area, A=\pi r^2, so the total area of the fountain is:
A (\text{fountain})=3.14\times6^2=113.04 m^2
The area of the statue base is:
A(\text{statue})=3.14\times1^2=3.14 m^2
So the area covered by water is:
A(\text{water}) = 113.04-3.14=109.9 m ^2
3 marks
