Question 1
LEVEL 8
Solve the inequality x^2 \leq 81.
Select the correct answer from the list below:
A: x < -9 \text{ and } x > 9
B: x \leq -9 \text{ and } x \geq 9
C: - 9\leq x \leq 9
D: - 9 < x < 9
CORRECT ANSWER: C: - 9\leq x \leq 9
WORKED SOLUTION:
Square root both sides of the equation. We get 2 square roots, positive and negative.
The range of values lie between and including -9 and 9, so
- 9\leq x \leq 9Question 2
LEVEL 8
Solve the inequality 4 x^2 > 144.
Select the correct answer from the list below:
A: x < -6 \text{ and } x > 6
B: x \leq -6 \text{ and } x \geq 6
C: - 6\leq x \leq 6
D: - 6 < x < 6
CORRECT ANSWER: A: x < -6 \text{ and } x > 6
WORKED SOLUTION:
Square root both sides of the equation. We get 2 square roots, positive and negative.
The range of values lie below -6 and above 6, so
x < -6 \text{ and } x > 6Question 3
LEVEL 8
Solve the inequality x^2+7x+12<0.
Select the correct answer from the list below:
A: x<3\text{ and }x>4
B: 3<x<4
C: -4<x<-3
D: x< -4\text{ and } x>-3
CORRECT ANSWER: C: -4<x<-3
WORKED SOLUTION:
To solve this inequality, we need to factorise the quadratic. Observing that 3\times 4=12 and 3+4=7, we get:
x^2+7x+12=(x+3)(x+4)<0If we treat this like an equality to start off with, we can use this to plot the quadratic as y=(x+3)(x+4). Note that the graph will cross the x-axis at x=-4 and x=-3.
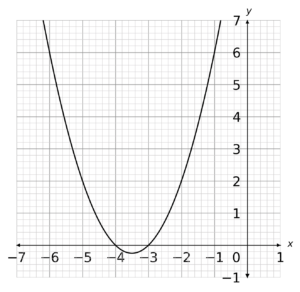
Now, we don’t want all these values we want all the ones that are (x+3)(x+4)<0. Because we plotted this as y=(x+3)(x+4), we can say that y<0 and so only want the bit below the y-axis.
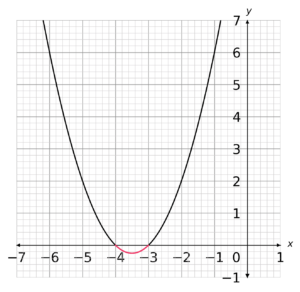
So, we can see that we only want the values of x that are between -4 and -3. Therefore, the solution to the inequality is:
-4<x<-3Question 4
LEVEL 8
Solve the inequality x^2+3x-10\geq0.
Select the correct answer from the list below:
A: x\leq-5 \text{ and }x\geq2
B: -5<x<2
C: -5\leq x\leq2
D: x\leq-2 \text{ and }x\geq5
CORRECT ANSWER: A: x\leq-5 \text{ and }x\geq2
WORKED SOLUTION:
To solve this inequality, we need to factorise the quadratic. Observing that (-2)\times5=10 and -2+5=3, we get:
x^2+7x+12=(x-2)(x+5)\geq0If we treat this like an equality to start off with, we can use this to plot the quadratic as y=(x-2)(x+5). Note that the graph will cross the x-axis at x=-5 and x=2.
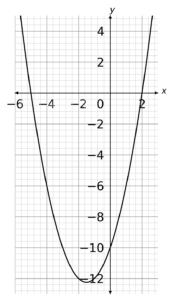
Now, we don’t want all these values we want all the ones that are (x-2)(x+5)\geq0. Because we plotted this as y=(x-2)(x+5), we can say that y\geq0 and so only want the bits above the y-axis.
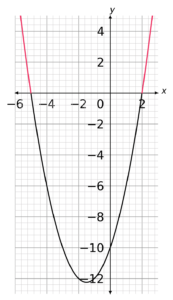
So, we can see that we only want the values of x that are less than -5 and bigger than 2. Therefore, the solution to the inequality is:
x\leq-5 \text{ and }x\geq2Question 5
LEVEL 8
Solve the inequality x^2-4x>0.
Select the correct answer from the list below:
A: -2<x<2
B: x<-2 \text{ and }x>2
C: x<0 \text{ and }x>4
D: 0<x<4
CORRECT ANSWER: C: x<0 \text{ and }x>4
WORKED SOLUTION:
To solve this inequality, we need to factorise the quadratic. Factorising here is pretty simple, as we can just pull out an x.
x^2-4x=x(x-4)>0If we treat this like an equality to start off with, we can use this to plot the quadratic as y=x(x-4). Note that the graph will cross the x-axis at x=0 and x=4.
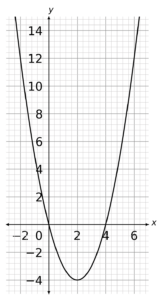
Now, we don’t want all these values we want all the ones that are x(x-4)>0. Because we plotted this as y=x(x-4), we can say that y>0 and so only want the bits above the y-axis.
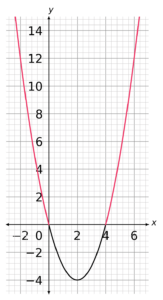
So, we can see that we only want the values of x that are less than 0 and bigger than 4. Therefore, the solution to the inequality is:
x<0 \text{ and }x>4