30 Proof (Higher)

Question 1

LEVEL 8

Given 2n+5, choose the statement that is always true.

n is an integer greater than 0.

Select the correct answer from the list below:

A: 2n+5 is always even

B: 2n+5 is always odd

C: 2n+5 is always prime

D: 2n+5 is always a multiple of 9

CORRECT ANSWER:    B: 2n+5 is always odd

WORKED SOLUTION:

The easiest way, usually, to show that something is false is to find counter examples. This will help us whittle down our answers. We can do this by substituting in some values for n.

\text{When }n=1\hspace{1cm}\rightarrow\hspace{1cm}2n+5=2(1)+5=2+5=7

\text{When }n=2\hspace{1cm}\rightarrow\hspace{1cm}2n+5=2(2)+5=4+5=9

\text{When }n=3\hspace{1cm}\rightarrow\hspace{1cm}2n+5=2(3)+5=6+5=11

\text{When }n=4\hspace{1cm}\rightarrow\hspace{1cm}2n+5=2(4)+5=8+5=13

\text{When }n=5\hspace{1cm}\rightarrow\hspace{1cm}2n+5=2(5)+5=10+5=15

And now, we can check each statement against these numbers, I use a tick for true and a cross for false.

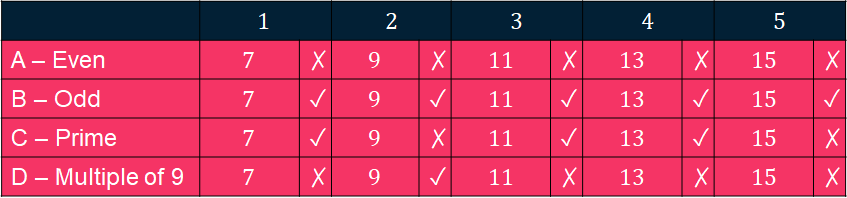
Here, our crosses represent the counter examples, so any row with a cross can’t be true. Only one row has all ticks, which is “B – Odd”. Although this is the only answer left so has to be the correct one, we haven’t proved that it is ALWAYS odd, we have only found some examples of it being true. Proving this is a simple task though:

2n is always even (this is how we define an even number).

5 is always going to be odd (it doesn’t change)

2n+5 will always be an odd number plus an even number, so will always be odd.

Question 2

LEVEL 8

Given 4n+8, choose the statement that is always true.

n is an integer greater than 0.

Select the correct answer from the list below:

A: 4n+8 is always odd

B: 4n+8 is always a multiple of 8

C: 4n+8 is always a multiple of 4

D: 4n+8 is always divisible by 5

CORRECT ANSWER:  C: 4n+8 is always a multiple of 4

WORKED SOLUTION:

The easiest way, usually, to show that something is false is to find counter examples. This will help us whittle down our answers. We can do this by substituting in some values for n.

\text{When }n=1\hspace{1cm}\rightarrow\hspace{1cm}4n+8=4(1)+8=4+8=12

\text{When }n=2\hspace{1cm}\rightarrow\hspace{1cm}4n+8=4(2)+8=8+8=16

\text{When }n=3\hspace{1cm}\rightarrow\hspace{1cm}4n+8=4(3)+12=12+8=20

\text{When }n=4\hspace{1cm}\rightarrow\hspace{1cm}4n+8=4(4)+8=16+8=24

\text{When }n=5\hspace{1cm}\rightarrow\hspace{1cm}4n+8=4(5)+8=20+8=28

And now, we can check each statement against these numbers, I use a tick for true and a cross for false.

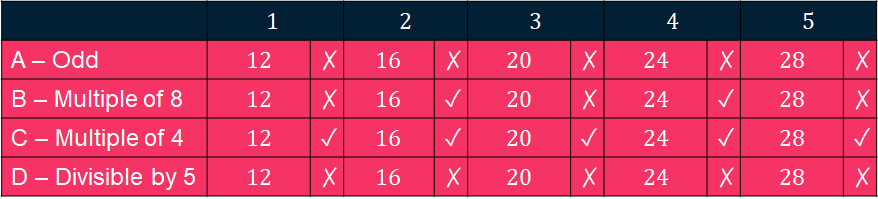
Here, our crosses represent the counter examples, so any row with a cross can’t be true. Only one row has all ticks, which is “C – Multiple of 4”. Although this is the only answer left so has to be the correct one, we haven’t proved that it is ALWAYS a multiple of 4, we have only found some examples of it being true. To prove this, we have to remember that for something to be a “multiple”, we have to be able to “take it out” or factorise. So, we need to see if we can take 4 out as a factor.

So, because we can’t 4 out, it must always be a multiple.

Question 3

LEVEL 8

Given the following rectangle, select the trues statement from the list below.

n is an integer greater than 0.

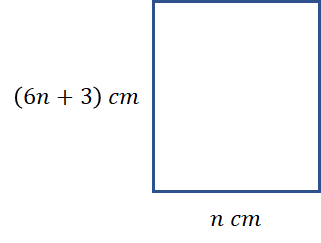
Select the correct answer from the list below:

A: The perimeter is always odd

B: The perimeter and area will always be equal

C: The area will always be a multiple of 3

D: The perimeter will always be smaller than the area

CORRECT ANSWER:   C: The area will always be a multiple of 3

WORKED SOLUTION:

The easiest way, usually, to show that something is false is to find counter examples. This will help us whittle down our answers. We can do this by substituting in some values for n. But, before we can do this, we need to find expressions for the perimeter and area.

\text{Perimeter }=6n+3+n+6n+3+n=14n+6

\text{Area }=(6n+3)\times n=6n^2+3n

And now we can substitute in some values of n into the expressions for perimeter and area.

\text{Perimeter When }n=1\hspace{1cm}\rightarrow\hspace{1cm}14n+6=14(1)+6=14+6=20

\text{Perimeter When }n=2\hspace{1cm}\rightarrow\hspace{1cm}14n+6=14(2)+6=28+6=34

\text{Perimeter When }n=3\hspace{1cm}\rightarrow\hspace{1cm}14n+6=14(3)+6=42+6=48

\text{Perimeter When }n=4\hspace{1cm}\rightarrow\hspace{1cm}14n+6=14(4)+6=56+6=62

\text{Perimeter When }n=5\hspace{1cm}\rightarrow\hspace{1cm}14n+6=14(5)+6=70+6=76

\text{Area When }n=1\hspace{1cm}\rightarrow\hspace{1cm}6n^2+3n=6(1)^2+3(1)=6(1)+3=6+3=9

\text{Area When }n=2\hspace{1cm}\rightarrow\hspace{1cm}6n^2+3n=6(2)^2+3(2)=6(4)+6=24+6=30

\text{Area When }n=3\hspace{1cm}\rightarrow\hspace{1cm}6n^2+3n=6(3)^2+3(3)=6(9)+9=54+9=63

\text{Area When }n=4\hspace{1cm}\rightarrow\hspace{1cm}6n^2+3n=6(4)^2+3(4)=6(16)+12=96+12=108

\text{Area When }n=5\hspace{1cm}\rightarrow\hspace{1cm}6n^2+3n=6(5)^2+3(5)=6(25)+15=150+15=165

We can now compare the perimeters and area when their n values are the same, because these will be the same rectangles. Putting these areas and perimeters into a table will help compare them.

We can now start looking for some counter examples.

A – Perimeter is always odd.

When n=1, the perimeter is even. A can’t be true.

In fact, \text{Perimeter }=14n+6=2(7n+3) so is always even

B – The perimeter and area will always be equal.

When n=1, the perimeter and area aren’t equal. B can’t be true.

In fact, they’re never equal. We can see that once n=3, then the area is bigger and is actually growing at a faster rate than the perimeter. We can however prove this algebraically as well

6n^2+3n=14n+6

6n^2+3n-14n=6

6n^2-11n=6

6n^2-11n-6=0

And now we can use the quadratic formula

If we just look at the rooty bit (\sqrt{b^2-4ac}) we get:

Because of this, for the perimeter and area to be equal, n has to be a non-integer, which isn’t allowed.

C – The area will always be a multiple of 3

Looking at our table, we can see that all of our areas are multiples of 3. However, this doesn’t prove it. To prove it, we just have to be able to take 3 out as a factor.

We can take 3 out, so the area will always be a multiple of 3.

D – The perimeter will always be smaller than the area.

Looking at n=1 we can see that the perimeter is bigger than the area, so this can’t be true.

Question 4

LEVEL 8

Given the expression (3n+3)^2+(5n-5)^2, select the true statement from the list below.

n is an integer greater than 0.

Select the correct answer from the list below:

A: (3n+3)^2+(5n-5)^2 is always even

B: (3n+3)^2+(5n-5)^2 is always odd

C: 3n+3 is a factor of (3n+3)^2+(5n-5)^2

D: (3n+3)^2+(5n-5)^2 is divisible by 8

CORRECT ANSWER:    A: (3n+3)^2+(5n-5)^2 is always even

WORKED SOLUTION:

A – (3n+3)^2+(5n-5)^2 is always even

To start we need to expand our two brackets.

(3n+3)^2=9n^2+18n+9

(5n-5)^2=25n^2-50n+25

(3n+3)^2+(5n-5)^2=9n^2+18n+9+25n^2-50n+25  

And now we can collect the like terms

9n^2+18n+9+25n^2-50n+25=34n^2-32n+34.

And finally, if this is even, we should be able to take 2 out as a factor

34n^2-32n+34 =2(17n^2-16n+17).

(3n+3)^2+(5n-5)^2 =2(17n^2-16n+17).

We were able to take 2 out as a factor, so this must be even. This is therefore our true statements.

Just to check, we need to disprove the other ones.

B – (3n+3)^2+(5n-5)^2 is always odd

Well, we just showed that (3n+3)^2+(5n-5)^2 is always even, so this can’t be even once. So this is definitely not true.

C – 3n+3 is a factor of (3n+3)^2+(5n-5)^2

To see if this is a factor, we need to be able to take this out as a factor. So let’s go from what we got in A.

(3n+3)^2+(5n-5)^2 =2(17n^2-16n+17).

To see if 3n+3 is a factor, we should be able to take it out of 2(17n^2-16n+17). However, this is the full factorisation, so 3n+3 can’t be a factor.

D – (3n+3)^2+(5n-5)^2 is divisible by 8

Using A again as the full factorisation, we can see that 8 can’t be taken out, so it can’t be a factor.

Question 5

LEVEL 8

Given the expression (4n-3)^2-(2n+5)^2, select the true statement from the list below.

n is an integer greater than 0.

Select the correct answer from the list below:

A: (4n-3)^2-(2n+5)^2 can be prime

B: (4n-3)^2-(2n+5)^2 is divisible by 6

C: (4n-3)^2-(2n+5)^2 is a multiple of n-4

D: (4n-3)^2-(2n+5)^2 is always a multiple of 5

CORRECT ANSWER:     C: (4n-3)^2-(2n+5)^2 is a multiple of n-4

WORKED SOLUTION:

To start we need to expand our two brackets.

(4n-3)^2=16n^2-24n+9

(2n+5)^2=4n^2+20n+25

(4n-3)^2-(2n+5)^2=16n^2-24n+9 - (4n^2+20n+25)

Multiplying through with the minus in front of the bracket

16n^2-24n+9 - (4n^2+20n+25) =16n^2-24n+9 - 4n^2-20n-25 .

And now we can collect the like terms

16n^2-24n+9 - 4n^2-20n-25=12n^2-44n-16 .

(4n-3)^2-(2n+5)^2=12n^2-44n-16 .

And now we can go through the other statements, showing that they aren’t true.

A – (4n-3)^2-(2n+5)^2 can be prime

We have:

(4n-3)^2-(2n+5)^2=12n^2-44n-16 .

However, we can factorise the right side of the equation, even by just pulling out a number:

12n^2-44n-16 =4(3n^2-11n-4).

So, we can clearly see that this will be a multiple of 4, and is therefore not going to be prime.

B – (4n-3)^2-(2n+5)^2 is divisible by 6

From A we had:

12n^2-44n-16 =4(3n^2-11n-4).

There is no way to get a 6 outside the bracket, so this can’t be divisible by 6.

C – (4n-3)^2-(2n+5)^2 is a multiple of n-4

To show that n-4 is a multiple of (4n-3)^2-(2n+5)^2 we need to be able to pull it outside the bracket (i.e. factorise).

12n^2-44n-16 =4(3n^2-11n-4).

So, let’s try and factorise that bracket on the right

3n^2-11n-4=(3n+1)(n-4).

Therefore, putting this back in, we get

12n^2-44n-16 =4(3n+1)(n-4) .

(4n-3)^2-(2n+5)^2=4(3n+1)(n-4) .

And so, n-4 is a factor, and this statement is true.

D – (4n-3)^2-(2n+5)^2 is always a multiple of 5

Again, using any of our previous factorisations, we can see that 5 can’t be taken out as a factor, (4n-3)^2-(2n+5)^2 is not a multiple of 5.

Question 6

LEVEL 8

Which of the following expressions is a multiple of 3?

Select the correct answer from the list below:

A: 13^{12} - 5^{15}

B: 13^{12} - 15^{5}

C: 12^{13} - 5^{15}

D: 12^{13} - 15^{5}

CORRECT ANSWER:    D: 12^{13} - 15^{5}

WORKED SOLUTION:

Take out a factor of 3 from each term:

12^{13} - 15^{5}

(12 \times 12^{12}) - (15 \times 15^{4})

(3 \times 4 \times 12^{12}) - (3 \times 5 \times 15^{4})

Factorise by 3:

We know that 3 multiplied by any number is a multiple of 3, so

12^{13} - 15^{5} = 3([4 \times 12^{12}] - [5 \times 15^{4}]) is a multiple of 3.

Question 7

LEVEL 8

Given the following expression

5^{37} - 287

Select the correct statement from the list below:

A: The answer is even and prime

B: The answer is odd and prime

C: The answer is even and not prime

D: The answer is odd and not prime

CORRECT ANSWER:    C: The answer is even and not prime

WORKED SOLUTION:

We know that \text{Odd} \times \text{Odd} = \text{Odd}, so

5^{37} is \text{Odd}

We also know that \text{Odd} - \text{Odd} = \text{Even},

so since 287 is also odd, we have that the answer is even.

Even numbers cannot be prime (except for 2), so the answer is even and not prime.