Q1

Above is a scale drawing of a Heterodontosaurus, what is the real life length of the dinosaur in metres?
Answer: 1.17 m
1.3 m
117 m
1.04 m
WORKING:
9\times13 cm =117 cm=1.17 m.
Q2
Pat is using a map with scale a 1:100000 to find the distance to the nearest petrol station.
The distance on the map is 11.8 cm.
What is the actual distance to the petrol station in km?
Answer: 11.8 km
Wrong Answers:
1.18 km
118 km
0.118 km
WORKING:
11.8\times100000=1180000 cm = 1180 m = 11.8 km.
Q3
The diagram shows the location of several towns.

Using the diagram, find the distance town F from town H.
Answer: 80 km
Wrong Answers:
90 km
70 km
100 km
WORKING:
There are 8 squares between town F and town H, so the distance is 8\times10 km = 80 km.
Q4
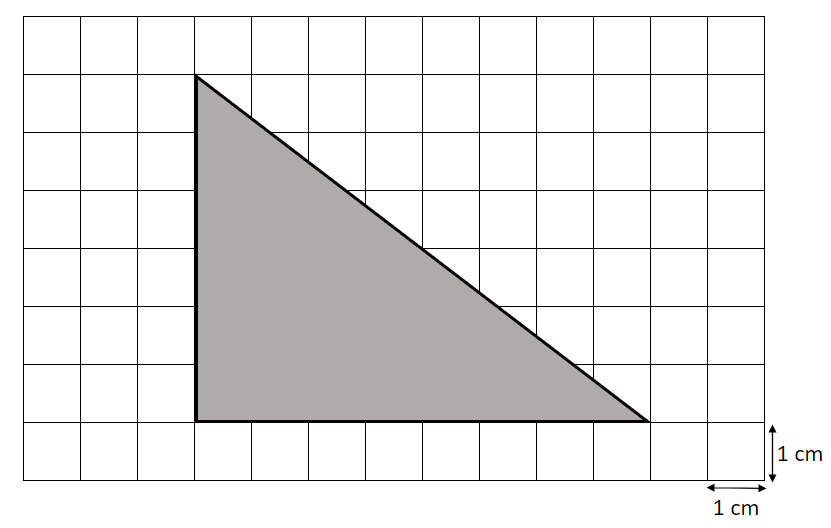
The diagram above shows a scale drawing of a right-angle triangle, which has height of 1.26 m and length of 1.68 m.
What scale has been used to make the scale drawing?
Answer: 1:21
Wrong Answers:
1:6
5:1
1:18
WORKING:
The height of the scale drawing is 6 cm.
The height of the original triangle is 1.26 m = 126 cm.
126\div6=21, hence the scale is 1:21.
Q5

The cuboid shown above has been drawn on 1 cm isometric paper.
Work out the volume of the cuboid.
Answer: 8 cm^3
Wrong Answers:
10 cm^3
28 cm^3
14 cm^3
WORKING:
Area of side front facing side = 2\times4=8 cm^2.
Volume of cuboid = 8\times1=8 cm^3.
Q6
A rectangle has height 1.75 m and width 1 m.
Which of the following scale drawings represents the rectangle with the scale 1:25?
Answer:

Wrong Answers:



WORKING:
If we convert the measurements for the original rectangle into cm, we get that the height is 175 cm and the width is 100 cm.
We can now use the scale 1:25 to calculate the height and width of the scale drawing.
175 cm \div 25=7 cm.
100 cm \div 25=4 cm.
So the height is 7 cm and the width is 4 cm.
Q7

A scale drawing of Ben’s bedroom is shown above.
Ben wants to put a wardrobe between his left wall and his window, he wants there to be at least a 25 cm gap on both sides of the wardrobe.
What is the maximum width (in metres) the wardrobe can be to fit Ben’s requirements?
Answer: 2.25 m
Wrong Answers:
2.75 m
2.5 m
2 m
WORKING:
From Ben’s requirements we can work out the maximum width of the wardrobe is (11-2)\times25=225 cm = 2.25 m.
Q8
The diagram shows the locations of several towns.

Using the diagram, find the distance of town C from town D.
Answer: 40 km
30 km
50 km
60 km
WORKING:
There are 4 squares between town C and town D, so the distance is 4\times10 km = 40 km.
