15. Angles in 2D Shapes (Practice Questions)

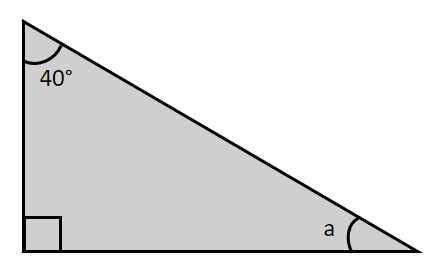
Work out the angle $a$ .

Answer: $50\degree$

$60\degree$

$40\degree$

$30\degree$

WORKING:

Angles in a triangle add up to $180\degree$ .

$180\degree-90\degree-40\degree=50\degree$ .

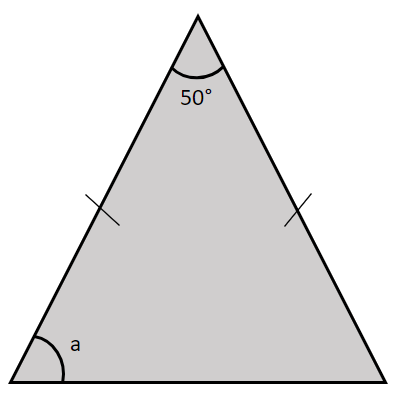
The triangle shown above is an isosceles triangle.

Find angle $a$ .

Answer: $65\degree$

Wrong Answers:

$50\degree$

$60\degree$

$70\degree$

WORKING:

As the triangle is an isosceles one. The two angles at the base of the triangle will be equal.

So $a=\dfrac{180\degree-50\degree}{2}=65\degree$ .

Below is a parallelogram.

Find angle $x$ .

Answer: $180\degree$

Wrong Answers:

$70\degree$

$100\degree$

$80\degree$

WORKING:

Because the shape is a parallelogram, $x+70+180$ .

$x=180-70=110\degree$ .

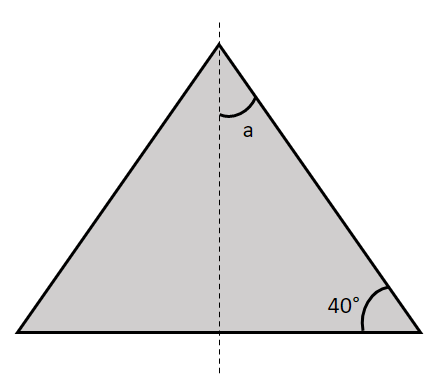
The diagram above shows a triangle with a line of symmetry.

Find angle $a$ .

Answer: $50\degree$

Wrong Answers:

$60\degree$

$90\degree$

$70\degree$

WORKING:

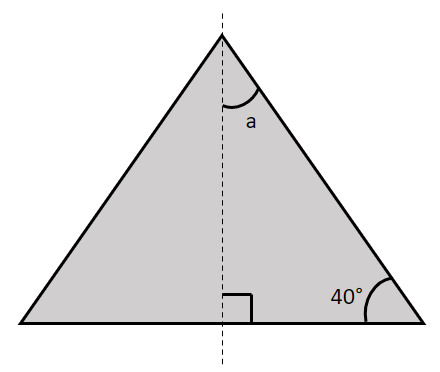
As the triangle has a line of symmetry, we can deduce that the larger triangle is made up of two smaller right-angle triangles.

Thus, $a=180-90-40=50\degree$ .

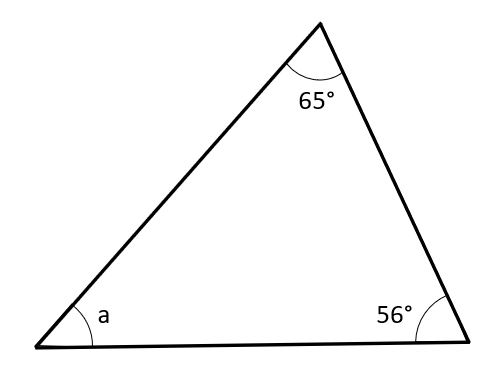
Find angle $a$ .

Answer: $59\degree$

Wrong Answers:

$56\degree$

$69\degree$

$49\degree$

WORKING:

Angles in a triangle add up to $180\degree$ .

$a=180-65-56=59\degree$ .

The diagram below shows a parallelogram.

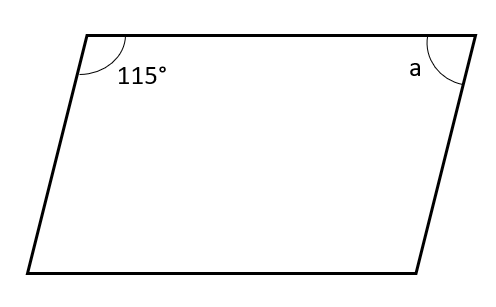
Find angle a.

Answer: $65\degree$

Wrong Answers:

$115\degree$

$75\degree$

$55\degree$

WORKING:

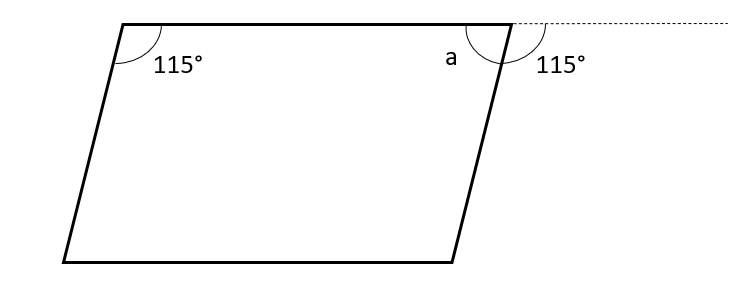
As shown in the diagram above, the exterior angle of $a$ is $115\degree$ .

Thus, $a=180-115=65\degree$ .

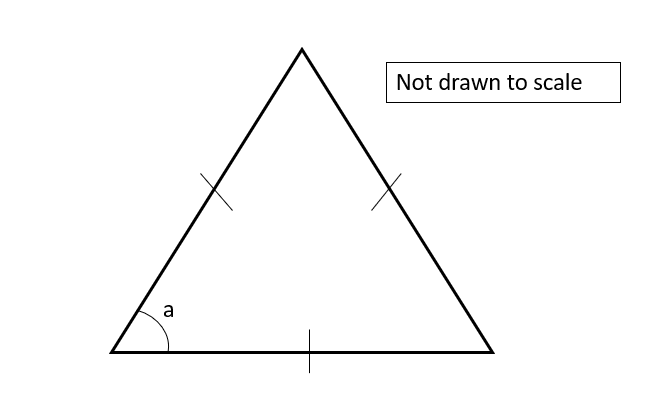
The diagram above shows an equilateral triangle.

Find angle $a$ .

Answer: $60\degree$

Wrong Answers:

$50\degree$

$70\degree$

$90\degree$

WORKING:

The interior angles in an equilateral triangle are equal.

Hence, $a=180\div3=60\degree$ .

The diagram below shows a quadrilateral.

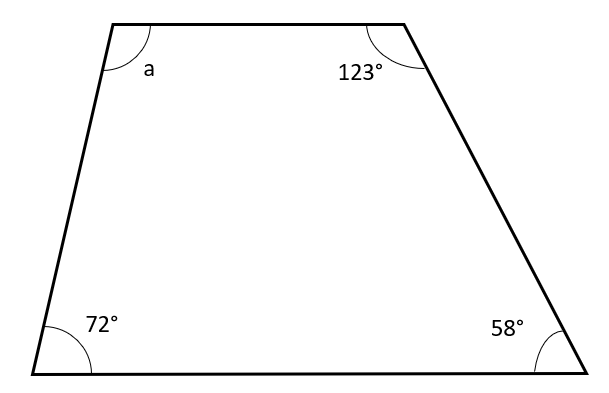
Find angle $a$ .

Answer: $107\degree$

Wrong Answers:

$97\degree$

$117\degree$

$101\degree$

WORKING:

Interior angles in a quadrilateral add up to $360\degree$ .

Thus, $a=360-72-58-123=107\degree$ .

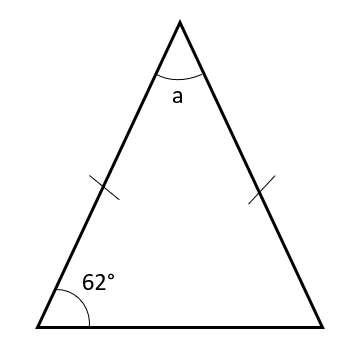
The diagram above shows an isosceles triangle.

Find angle $a$ .

Answer: $56\degree$

Wrong Answer:

$62\degree$

$66\degree$

$54\degree$

WORKING:

As the triangle is an isosceles one. The two angles at the base of the triangle will be equal.

So we can deduce that the third angle in the triangle is $62\degree$ .

Thus, $a=180-(62\times2)=56\degree$ .

Q10

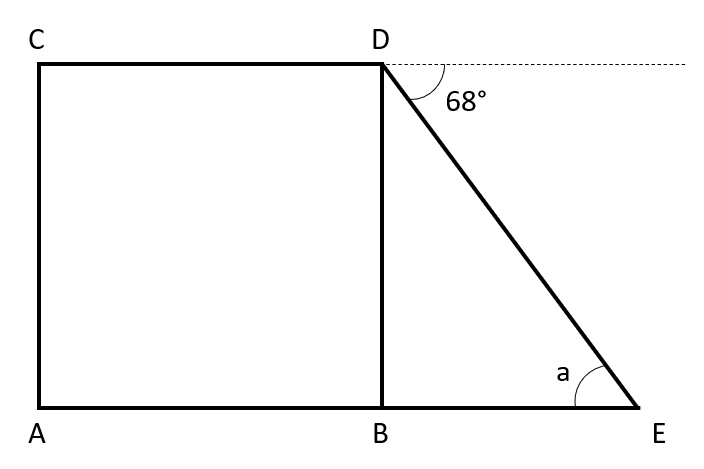
The diagram above shows the square ACDB and a triangle DBE, where ABE is a straight line.

Find angle $a$ .

Answer: $68\degree$

Wrong Answers:

$22\degree$

$58\degree$

$48\degree$

WORKING:

Because ACDB is a square, we know that all four angles in the square are $90\degree$ .

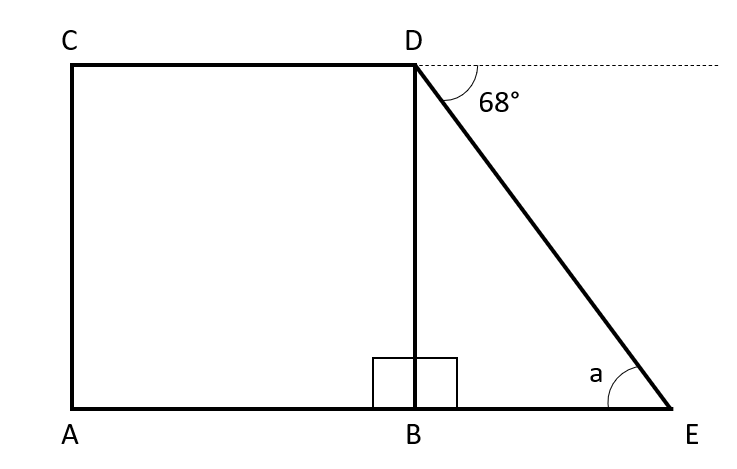
Therefore we can deduce that the triangle BDE is a right-angle triangle (as shown in the diagram above).

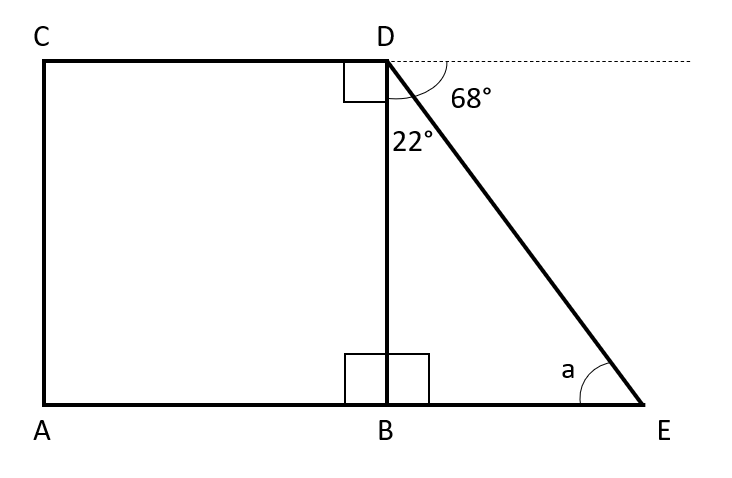
We can also find the third angle of the triangle by using the fact that angles on a straight line sum to $180\degree$ .

As shown on the diagram, $180-68-90=22\degree$ .

Finally, to find $a$ , we use the fact that angles in a triangle sum to $180\degree$ .

$a=180-90-22=68\degree$ .