Question 1: [3 marks]
A diagram of a rectangular garden is shown below.
Each length is measured to the nearest 0.1 m
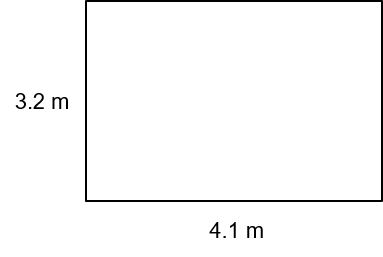
Calculate the minimum and maximum possible values for the area of the garden.
Give your answers to 1 decimal place.
Answer type: Multiple answers type 1
ANSWER:
13.5\leq Area < 12.813\leq Area < 14 3.15\leq Area < 3.25 4.05\leq Area < 4.15
WORKING:
Max area = 4.15 \times 3.25 = 13.4875 = 13.5 (1 dp)
Min area = 4.05 \times 3.15 = 12.7575 = 12.8 (1 dp)
Question 2: [2 marks]
The distance from Sarah’s house to Peter’s house is 230 miles measured to the nearest 10 miles.
Sarah took exactly 4 hours to complete this journey.
Sarah says: “My average speed was 60 mph for the journey to Peter’s house”
Is Sarah correct?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: B: No
WORKING: Min speed = \dfrac{225}{4} = 56.25
Max speed = \dfrac{235}{4} = 58.75
The average speed is between 56.25 and 58.75, not 60.
Question 3:
x and y are measured to 3.42 m and 0.92 m, both correct to the nearest 0.01 m.
Question 3(a): [2 marks]
Find the upper and lower bounds of x and y.
Answer type: Multiple answers type 1
ANSWER:
x min =3.415 m
x max =3.425 m
y min =0.915 m
y max =0.925 m
Question 3(b): [2 marks]
z = \dfrac{1}{x} + y.
Find the maximum and minimum possible values of z.
Give answers to 3 decimal places.
Answer type: Multiple answers type 1
ANSWER:
z min =1.207 m
z max =1.218 m
WORKING:
z min = \dfrac{1}{3.425} + 0.915 = 1.207 (3 dp)
z max = \dfrac{1}{3.415} + 0.925 = 1.218 (3 dp)
Question 4:
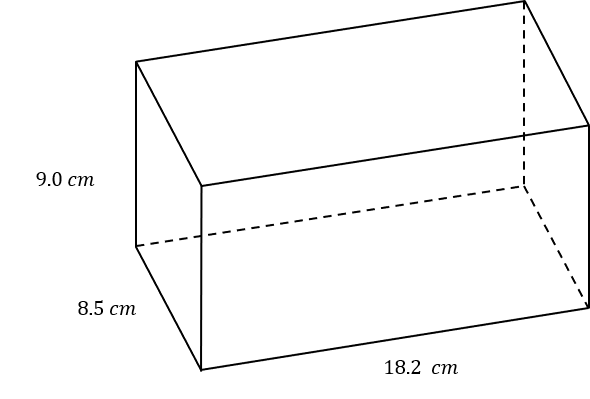
The dimensions of a cuboid container are shown below.
Each length has been measured to 1 decimal place.
Question 4(a): [2 marks]
Calculate the upper bound for the volume of the cuboid.
Give you answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 1412.14
WORKING: Upper bound = 9.05 \times 8.55 \times 18.25 = 1412.14 (2 dp)
Question 4(b): [2 marks]
Joe has a bucket containing 1370 cm^3 of water measured to the nearest 10 cm^3
Joe Says: “If I tip my bucket of water in the cuboid container, it will never overflow”
Is Joe correct?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: B: No
WORKING:
Upper bound of water is 1375 cm^3.
Lower bound of the bucket is 8.95 \times 8.45 \times 18.15 = 1372.63 cm^3.
The container could overflow, since the upper bound of the water is greater than the lower bound of the container volume.
So Joe is incorrect.
Question 5:
A ball is dropped from a height of d meters.
The time, t seconds, taken for the ball to reach the ground is given by
t = \sqrt{\dfrac{2d}{g}}
where g is the acceleration due to gravity.
g = 9.8 \, m/s^2 correct to 2 significant figures.
d = 12.4 \, m correct to 3 significant figures.
Question 5(a): [1 mark]
Find the lower bound of d.
Answer type: Simple text answer
ANSWER: 12.35 m
Question 5(b): [3 marks]
Find the minimum value of t. Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 1.58
WORKING: t = \sqrt{\dfrac{2 \times 12.35}{9.85}} = 1.584 = 1.58 (2 dp)
We need to choose the lower bound of d, since it is on the top of the fraction, and the upper bound of g, since it is on the bottom of the fraction. This gives us the lower bound of t.
Question 6: [3 marks]
x and y are measured to 53.4 and 33.9 both correct to 3 significant figures.
Question 6(a): [2 marks]
Find the upper and lower bounds of x and y.
Answer type: Multiple answers type 1
ANSWER:
=53.35 x \leq
x > =53.45
=33.85 y \leq
y > =33.95
Question 6(b): [2 marks]
z = \sqrt{xy}.
Find the maximum and minimum possible values of z.
Give answers to 4 significant figures.
Answer type: Multiple answers type 1
ANSWER:
=42.50z \leq
z > =42.60
WORKING:
z min = \sqrt{53.35 \times 33.85} = 42.50 (4 sf)
z max = \sqrt{53.45 \times 33.95} = 42.60 (4 sf)
