Question 1:
Here are the 5 first terms of a linear sequence.
,7, 11, 15, 19, 23
1(a):
Write down the next two terms of the sequence.
ANSWER: Multiple Answers (Type 1)
Answer: 27 & 31
Workings:
Sequence increases by 4 for each term
6^{th} term: 23+4=27
7^{th} term: 27+4=31
Marks = 2
1(b):
Give the n^{th} term for the sequence.
ANSWER: Multiple Choice (Type 1)
A: 3n+3
B: 4n+2
C: 4n+3
D: 4n+1
Answer: C
Workings:
Difference between terms n and n+1 is 4
Using n=1
7-4n =7-4\times 1 = 3
n^{th} term is 4n+3
Marks = 1
Question 2:
The n^{th} term of a sequence can be found using,
2n+2where n is the position in the sequence.
2(a):
Write the first 5 terms of the sequence.
ANSWER: Multiple Answers (type 1)
Answer: 4,6,8,10,12
Workings:
For n=1: n^{th} term = 2 \times 1 + 2 = 4
Repeat for n=2,3,4,5
Marks= 2
2(b):
Work out the 100^{th} term in this sequence.
ANSWER: Simple Text Answer
Answer: 202
Workings:
2 \times 100 +2 = 202
Marks= 1
2(c):
Explain why the number 155 will not occur in this sequence.
ANSWER: Multiple Choice (Type 1)
A: 155 is a multiple of 2.
B: The sequence won’t go that high.
C: All terms in the sequence are even.
D: All terms in the sequence are odd.
Answer: All terms in the sequence are even.
Workings:
Every term multiplied by 2 gives an even value.
Adding on 2 will give another even number.
Marks= 1
Question 3:
Here are the first 5 terms of a linear sequence,
5, 9, 13,17,21
3(a):
Write down the next term of the sequence.
ANSWER: Simple Text Answer
Answer: 25
Workings:
Sequence increases by 4 each term.
21+5=25
Marks = 1
3(b):
Find the n^{th} term of this sequence.
ANSWER: Multiple Choice (Type 1)
A:3n+1
B: 4n+1
C:4n+2
D:3n+2
Answer: B
Workings:
Sequences by 4 each time.
5-4n=1 for n=1
n^{th} term is 4n+1
Marks=2
3(c):
Hence, or otherwise, find the 47^{th} term in this sequence.
ANSWER: Simple Text Answer
Answer: 189
Workings:
Substitute n=47 into the n^{th} term
4 \times 47 +1 = 189
Marks= 1
Question 4:
Here are the first 5 terms of a linear sequence.
3, 9, 15, 21, 27
4(a):
Write down the next term of the sequence.
ANSWER: Simple Text Answer
Answer: 33
Workings:
Sequence increases by 6 each term
27+6=33
Marks= 1
4(b):
Find the n^{th} this sequence.
ANSWER: Multiple Choice (Type 1)
A: 6n-3
B: 6n-2
C: 6n-1
D: 6n
Answer: A
Workings:
Increasing by 6 each time so 6n gives common difference
For n=1:
3-6 \times 1 = -3
Gives 6n-3 as n^{th} term
Marks= 2
4(c)
Hence, or otherwise, find the 9^{th} term in this sequence.
ANSWER: Simple Text Answer
Answer: 51
Workings:
6 \times 9 - 3 = 51
Marks=1
Question 5:
The n^{th} term of a sequence can be found using
4n -2where n is the position in the sequence.
5(a):
Write the first 5 terms of the sequence.
ANSWER: Multiple Answers (Type 1)
Answer: 2,6,10,14,18
Workings:
Substitute each of n=1,2,3,4,5 into the n^{th} term
For n=1:
4 \times 1 - 2 = 2
Marks= 2
5(b):
Find the position number for the term with the value 82.
ANSWER: Simple Text Answer
Answer: 21
Workings:
4n-2 = 82
4n=84
n=21
Marks= 2
5(c):
Explain how you know whether the number 80 will occur in this sequence or not.
ANSWER: Multiple Choice (Type 1)
A: It will not because 82 is in the sequence and therefore 78.
B: It will not because 82 is not a multiple of 4.
C: It will because 80 is a multiple of 4.
D: It will because 80 is even.
Answer: A
Workings:
We know that 82 is in the sequence, so the term before it is 78.
Therefore 80 is not in the sequence
Marks= 1
Question 6:
Each table can fit a maximum of four chairs. Once tables are pushed together the chairs where the tables join can no longer be placed.

The image above shows the layout of different numbers of tables with chairs.
6(a)
Complete the table below with the correct number of chairs for tables.
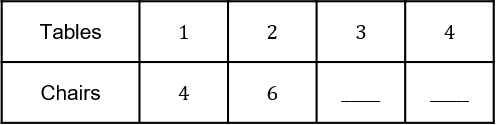
ANSWER: Multiple Answers (Type 1)
Answer: 8 & 10
Workings:
When a table is added on only 2 additional spaces for chairs become available.
Marks= 2
6(b)
Sara’s street party will need chairs for 115 people.
Chairs cost £2.00 each and tables cost £10.00.
Work out how many tables Sara will need and use this to calculate the total cost in £.
ANSWER: Simple Text Answer
Answer: 800
Workings:
n^{th} term =2t + 2
2t+2=115
2t=113
t=56.5 so 57 tables are needed
Cost =(57 \times 10)+(115 \times 2)=570+230 = £800.00
Marks= 4
