Question 1
Solve x - 2 = 0.
Answer: Multiple Choice (Type 1)
A: x = - 2
B: x = 0
C: x = \dfrac{1}{2}
D: x = 2
Answer: D
Marks = 1
Question 2
5a = 13.
What is the value of 15a?
ANSWER: Simple text answer
Answer: 39
Workings:
15 \div 5 = 3
3 \times 13 = 39
Marks = 2
Question 3
Given that 2x - 3 = 7
What is the value of x?
ANSWER: Simple text answer
Answer: 5
Workings:
2x = 10
x = 5
Marks = 2
Question 4
Solve the following equations:
4(a) 3x - 2 = 9
ANSWER: Fraction
Answer: x = \dfrac{11}{3}
Workings:
3x = 11
x = \dfrac{11}{3}
Marks = 2
4(b) 2x - 5 + x - 2 = 5
ANSWER: Simple text answer
Answer: x = 4
Workings:
3x -7 = 5
3x = 12
x = 4
Marks = 2
4(c) 6x - 2 = 4x + 14
ANSWER: Simple text answer
Answer: x = 8
Workings:
2x = 16
x = 8
Marks = 2
4(d) \dfrac{x}{3}-5 = 7
ANSWER: Simple text answer
Answer: x = 36
Workings:
\dfrac{x}{3} = 12
x = 36
Marks = 2
Question 5
Susie knows that the length of the rectangle below is 4 cm greater than the width.
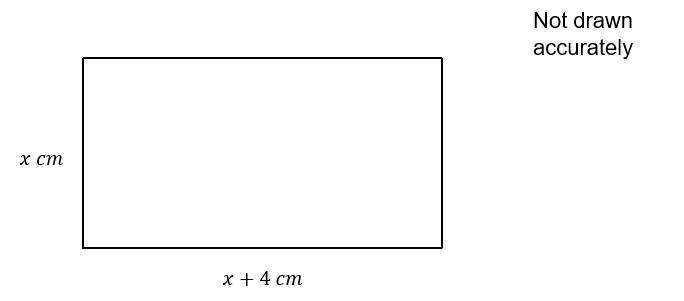
5(a) Write down an expression for the perimeter
ANSWER: Simple text answer
Answer: 4x + 8
Workings:
2(x) + 2(x + 4)
= 4x + 8
Marks = 1
5(b) Given that the perimeter is 32 cm , find the value of x.
ANSWER: Simple text answer
Answer: x = 6
Workings:
4x + 8 = 32
4x =24
x = 6
Marks = 2
Question 6
Mackey’s milk company use the following formula to calculate their sale price:
\bm{C} = \bold{55}\bm{P_f} + \bold{40}\bm{P_s}
\it{C} = cost (in pence)
\it{P_f} = pints of full fat milk
\it{P_s} = pints of skimmed milk
6(a) Terry gets 1 pint of full fat milk and 2 pints of skimmed milk.
Work out the cost in pounds (£).
ANSWER: Simple text answer
Answer: £1.35
Workings:
C = 55(1) + 40(2) = 135p
135p = £1.35
Marks = 2
6(b) Dickie’s Dairy Services Ltd charges the following for their milk.
\bm{C} = \bold{25}\bm{P_f} + \bold{15}\bm{P_s} + \bold{90}
How much would it cost Terry for an order in Dickie’s Dairy Services Ltd if he bought the same amount that he did at Mackey’s milk?
ANSWER: Simple text answer
Answer: £1.45
Workings:
C = 25(1) + 15(2) + 90 = 145p
145p = £1.45
Marks = 2
Question 7
Bill calculates his income tax T based on his earnings E in the following way
Bill is not taxed on the first £12,500 he earns.
He is taxed 25% on the rest of his earnings.
7(a) Which of the following equations links T and E?
ANSWER: Multiple Choice (Type 1)
A: T = \dfrac{1}{4}(E + 12500)
B: T = \dfrac{1}{4}(E - 12500)
C: T = \dfrac{12500}{4} +E
D: T = \dfrac{E}{4} + 12500
Answer: B
Workings:
Tax is 25% of (E - 12500)
T = \dfrac{1}{4}(E - 12500)
Marks = 2
7(b) Bill payed £5,500 tax this year.
How much did his earnings amount to?
ANSWER: Simple text answer
Answer: £34500
Workings:
5500 = \dfrac{1}{4}(E - 12500)
22000 = E - 12500
E = £34500
Marks = 2
