Question 1:
Midpoints are points that are found exactly half way along a line.
Question 1(a): [1 mark]
Find the x and y coordinates of the midpoint for the line AB , shown below.
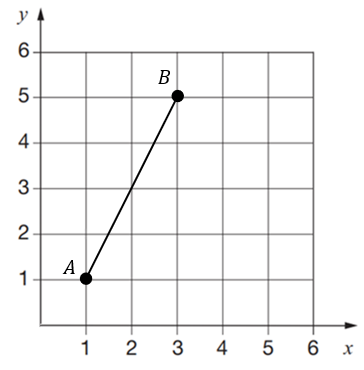
Answer type: Multiple answers type 1
ANSWER: x = 2, y = 3
WORKING:
x = \dfrac{1+3}{2} = 2
y = \dfrac{1+5}{2} = 3
Question 1(b): [1 mark]
Find the x and y coordinates of the midpoint for the line CD , shown below.

Answer type: Multiple answers type 1
ANSWER: x = 0, y = 0
WORKING:
x = \dfrac{-3+3}{2} = 0
y = \dfrac{-3+3}{2} = 0
Question 1(c); [1 mark]
Find the x and y coordinates of the midpoint for the line EF , shown below.
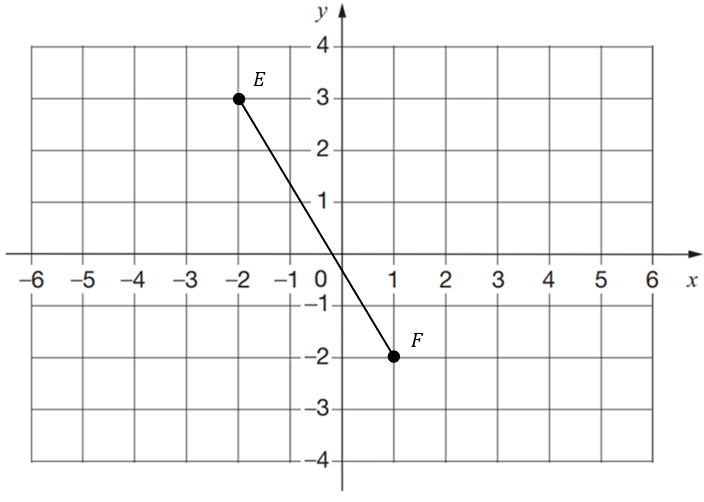
Answer type: Multiple answers type 1
ANSWER: x = -0.5, y = 0.5
WORKING:
x = \dfrac{-2+1}{2} = -0.5
y = \dfrac{-2+3}{2} = 0.5
Question 2(a): [1 mark]
The points A and B form a line segment AB. M is the midpoint of AB.
A = (5, 10), B = (17,8)
Find the x and y coordinates of M.
Answer type: Multiple answers type 1
ANSWER: x = 11, y = 9
WORKING:
x = \dfrac{5+17}{2} = 11
y = \dfrac{10+8}{2} = 9
Question 2(b): [1 mark]
The points C and D form a line segment CD. M is the midpoint of CD.
C = (-2, -10), D = (-7,-14)
Find the x and y coordinates of M.
Answer type: Multiple answers type 1
ANSWER: x = -4.5, y = -12
WORKING:
x = \dfrac{-2-7}{2} = - 4.5
y = \dfrac{-10-14}{2} = -12
Question 2(c): [1 mark]
The points E and F form a line segment EF. M is the midpoint of EF.
E = (0, -10), F = (-6,0)
Find the x and y coordinates of M.
Answer type: Multiple answers type 1
ANSWER: x = -3, y = -5
WORKING:
x = \dfrac{0-6}{2} = -3
y = \dfrac{-10+0}{2} = -5
Question 3: [2 marks]
A and B are two points of a square ABCD.

Choose a possible sets of coordinates for C and D.
Answer type: Multiple choice type 2
1: C = (5,0) and D = (-2, 3)
2: C = (1,4) and D = (2, -1)
3: C = (4,1) and D = (2, -1)
4: C = (1,4) and D = (-1, 2)
ANSWER: 4: C = (1,4) and D = (-1, 2)
Question 4: [2 marks]
The midpoints of the lines AB, BC and AC are X, Y and Z respectively.

Which of the following shapes is the correct representation?
Answer type: Multiple choice type 2
A: 
B: 
C: 
D: 
ANSWER:
C: 
WORKING: X(2,-5), Y(-5,0), Z(2, -9)
Question 5:
Calculate the midpoint of the line segment between the following sets of points.
Question 5(a): [2 marks]
(-2,3) and (10,7)
Answer type: Multiple choice type 1
A: (4,5)
B: (5,4)
C: (0.5, 8.5)
D: (0,0)
ANSWER: A: (4,5)
WORKING:
The x and y coordinates of the midpoint are
x = \dfrac{-2+10}{2} = 4
y = \dfrac{3+7}{2} = 5
Hence, the midpoint is (4,5)
Question 5(b): [2 marks]
(-5,-7) and (-8,7)
Answer type: Multiple choice type 1
A: (-6.5,0)
B: (0,-6.5)
C: (-6, -0.5)
D: (0,0)
ANSWER: A: (-6.5,0)
WORKING:
The x and y coordinates of the midpoint are
x = \dfrac{-5-8}{2} = -6.5
y = \dfrac{-7+7}{2} = 0
Hence, the midpoint is (-6.5,0)
Question 5(c): [2 marks]
(-3.5,1) and (-2,8.5)
Answer type: Multiple choice type 1
A: (-2,75 ,4.75)
B: (2,75 , -4.75)
C: (-2,25 ,4.25)
D: (4,75 , -2.75)
ANSWER: A: (-2,75 ,4.75)
WORKING:
The x and y coordinates of the midpoint are
x = \dfrac{-3.5-2}{2} = -2.75
y = \dfrac{1+8.5}{2} = 4.75
Hence, the midpoint is (-2,75 ,4.75)
Question 6:
M is the midpoint of the line segment PQ in each of the following questions.
Find the coordinates of Q in each case, when:
Question 6(a): [2 marks]
P = (1,5) and M = (-2,-2)
Answer type: Multiple choice type 1
A: Q = (-5, -9)
B: Q = (-0.5, 1.5)
C: Q = (-9, -5)
D: Q = (3,1)
ANSWER: A: Q = (-5, -9)
WORKING:
We want to find the coordinates (x,y) of Q, by reversing the calculation for finding the midpoint.
(-2,-2) = \left(\frac{1+x}{2}, \frac{5+y}{2} \right)
(-4,-4) = (1+x , 5+y)
(-5, -9) = (x, y)
Hence, the coordinates of Q are (-5,-9)
Question 6(b): [2 marks]
P = (-3,-6) and M = (8,-11)
Answer type: Multiple choice type 1
A: Q = (19, -16)
B: Q = (-19, 16)
C: Q = (16, -19)
D: Q = (2.5, -8.5)
ANSWER: A: Q = (19, -16)
WORKING:
We want to find the coordinates (x,y) of Q, by reversing the calculation for finding the midpoint.
(8, -11) = \left(\frac{x-3}{2}, \frac{y-6}{2} \right)
(16,-22) = (x-3 , y-6)
(19, -16) = (x, y)
Hence, the coordinates of Q are (19,-16)
