Question 1(a): [3 marks]
Point D lies on a line AB such that AD is \dfrac{2}{3} of the total length of AB.
Given that A(2, 4) and B(17, 13), find the x and y coordinates of the point D.
Answer type: Multiple answers type 1
ANSWER: x = 12, y = 10.
WORKING:
17 - 2 = 15 ; 13 - 4 = 9
15 \times \dfrac{2}{3} = 10 ; 9 \times \dfrac{2}{3} = 6
2 + 10 = 12 ; 4 + 6 = 10
(12, 10)
Question 1(b): [3 marks]
Point E lies on a line AB such that AD is \dfrac{5}{7} of the total length of AB.
Given that A(0, 10) and B(-21, -25), find the x and y coordinates of the point D.
Answer type: Multiple answers type 1
ANSWER: x = - 15, y = - 15.
WORKING:
-21 - 0 = - 21 ; -25 -10 = -35
-21 \times \dfrac{5}{7} = - 15 ; - 35 \times \dfrac{5}{7} = - 25
0 + (-15) = -15 ; 10 + (-25) = - 15
(- 15, - 15)
Question 2:
Point C lies on the line segment AB. C is such that the ratio AC:CB = 1:2.

Question 2(a): [2 marks]
What are the x and y coordinates of the point C?
Answer type: Multiple answers type 1
ANSWER: x = - 2, y = -2.
WORKING:
A(-4,-5) , B(2,4)
2 - (- 4) = 6 ; 4 - (-5) = 9
6 \times \dfrac{1}{3} = 2 ; 9 \times \dfrac{1}{3} = 3
- 4 + 2 = - 2 ; - 5 + 3 = - 2
( -2, -2)
Question 2(b): [2 marks]
Another point X lies on the line segment AB.
This divides the line segment in the ratio AC:CX:XB = 2:1:3
What are the x and y coordinates of the point X?
Answer type: Multiple answers type 1
ANSWER: x = - 1, y = - 0.5.
WORKING:
C(-2,-2), B(2,4)
CX:XB = 1:3
-2 - 2 = -4; -2 - 4 = -6
4 \times \dfrac{1}{4} = 1 ; 6 \times \dfrac{1}{4} = 1.5
-2 + 1 = -1 ; -2 + 1.5 = -0.5
(-1 , -0.5)
Question 3:
F lies on a line AB such that AF is \dfrac{3}{4} of the length of AB.
Question 3(a): [2 marks]
Given that A(0,0) and B(20,-8), find the x and y coordinates of the point F.
Answer type: Multiple answers type 1
ANSWER: x = 15, y = - 6
WORKING:
Change in x = +20, Change in y = -8.
20 \times \dfrac{3}{4} = 15 ; - 9 \times \dfrac{3}{4} = - 6
(15, - 6)
Question 3(b): [1 mark]
G lies on AF such that AG:GF=1:2.
Write down the ratio AG:GF:FB, in terms of a:b:c.
Answer type: Multiple answers type 1
ANSWER: a = 1, \, b = 2, \, c = 1
Question 3(c): [2 marks]
Hence find the x and y coordinates of G.
Answer type: Multiple answers type 1
ANSWER: x = 5, y = - 2
WORKING:
A(0,0) and F(15,-6)
Change in x = + 15 ; Change in y = - 6.
15 \times \dfrac{1}{3} = 5 ; - 6 \times \dfrac{1}{3} = - 2
(5, - 2)
Question 4: [2 marks]
X is a point on the line segment AB.
Y is a point on the line segment CD.
AX:XB = CY:YD = 1:2.

Which of the following graphs is the correct representation of the line XY.
Answer type: Multiple choice type 2
A: 
B: 
C: 
D: 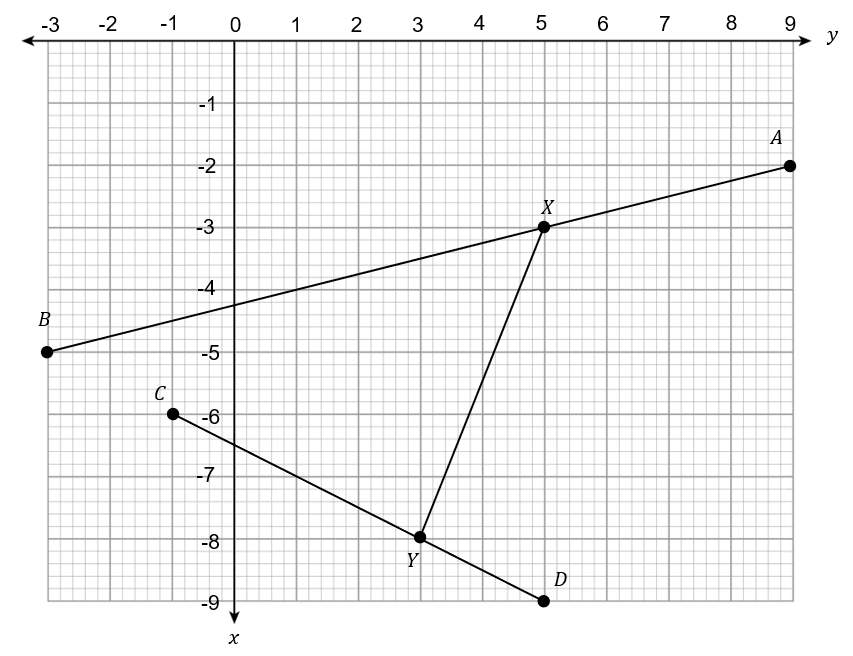
ANSWER:
A: 
WORKING:
X(5, -3) ; Y(1, -7)
y \text{intercept} = - 8
\text{Gradient} = 1
y = x - 8
Question 5:
The point R lies on the line segment PQ such that the ratio PR:RQ = 1:4
The point T lies on the line segment QS such that the ratio QT:TS = 3:1
The point U lies on the line segment TR such that the ratio TU:UR = 1:2
Given that P = (2,1), Q = (12,6) and S = (0,10):
Question 5(a): [3 marks]
Find the coordinates of the point R
Answer type: Multiple choice type 1
A: (4,2)
B: (2,4)
C: (10,5)
D: (5,10)
ANSWER: A: (4,2)
WORKING:
In a ratio of 1:4 there are 5 parts in total, and the distance from P to R constitutes 1 of those parts. Therefore, the distance from P to R counts for \frac{1}{5} of the total distance between P and Q.
First, the x coordinates: 12-2=10, then
\frac{1}{5}\times 10 = 2
Adding this to the x coordinate of P, gives the x coordinate of R:
2+2=4
Second, the y coordinates: 6-1=5, then
\frac{1}{5}\times 5=1
Adding this to the y coordinate of P, gives the y coordinate of R:
1+1=2
Therefore, the coordinates of R are (4,2)
Question 5(b): [3 marks]
Find the coordinates of the point T
Answer type: Multiple choice type 1
A: (3,9)
B: (9,3)
C: (9,7)
D: (-2,-6)
ANSWER: A: (3,9)
WORKING:
In a ratio of 3:1 there are 4 parts in total, and the distance from Q to T constitutes 3 of those parts. Therefore, the distance from Q to T counts for \frac{3}{4} of the total distance between Q and S.
First, the x coordinates: 0-12=-12, then
\frac{3}{4}\times (-12) = -9
Adding this to the x coordinate of Q, gives the x coordinate of T:
12-9=3
Second, the y coordinates: 10-6=4, then
\frac{3}{4}\times 4=3
Adding this to the y coordinate of Q, gives the y coordinate of T:
6+3=9
Therefore, the coordinates of T are (3,9)
Question 5(c): [3 marks]
Find the coordinates of the point U
Answer type: Multiple choice type 1
A: \left(\dfrac{10}{3}, \dfrac{20}{3} \right)
B: \left(\dfrac{23}{4}, \dfrac{13}{4} \right)
C: (3,9)
D: (4,2)
ANSWER: A: \left(\dfrac{10}{3}, \dfrac{20}{3} \right)
WORKING:
In a ratio of 1:2 there are 3 parts in total, and the distance from T to U constitutes 1 of those parts. Therefore, the distance from T to U counts for \frac{1}{3} of the total distance between T and R.
First, the x coordinates: 4-3=1, then
\frac{1}{3}\times (1) = \frac{1}{3}
Adding this to the x coordinate of T, gives the x coordinate of U:
3 + \frac{1}{3} = \frac{10}{3}
Second, the y coordinates: 2-9=-7, then
\frac{1}{3}\times (-7)= - \frac{7}{3}
Adding this to the y coordinate of T, gives the y coordinate of U:
9 - \frac{7}{3} = \frac{20}{3}
Therefore, the coordinates of T are \left(\dfrac{10}{3}, \dfrac{20}{3} \right)
Question 6: [4 marks]
Point B lies on a line AC such that AB:BC = 3:2
Given that A = (3,q), B = (9,4q) and C = (p,6), find the values of p and q
Answer type: Multiple answers type 1
ANSWER:
p = 13
q = 1
WORKING:
In a ratio of 3:2 there are 5 parts in total, and the distance from A to B constitutes 3 of those parts. Therefore, the distance from A to B counts for \frac{3}{5} of the total distance between A and C.
First, the x coordinates of B:
p-3, then
\dfrac{3}{5}\times (p-3) = \dfrac{3p-9}{5}Adding this to the x coordinate of A, gives the x coordinate of B:
3 + \dfrac{3p-9}{5} = \dfrac{3p+6}{5}
We know that the x coordinate of B is 9, therefore we can form an equation and solve for p:
\dfrac{3p+6}{5} = 9
3p+6=45
3p=39
p=13
Second, the y coordinates of B:
6-q, then
\dfrac{3}{5}\times (6-q)= \dfrac{18-3q}{5}Adding this to the y coordinate of A, gives the y coordinate of B:
q + \dfrac{18-3q}{5} = \dfrac{18+2q}{5}
We know that the y coordinate of B is 4q, therefore we can form an equation and solve for q:
\dfrac{18+2q}{5}=4q
18+2q=20q
18q=18
q=1
