Question 1:
Answer the following questions.
Question 1(a): [1 mark]
Which of the following equations represents a circle with a centre at (0,0) and a radius of 8?
Answer type: Multiple choice type 1
A: x^2 + y^2 = 16
B: (x+8)^2 + y^2 = 0
C: x^2 + y^2 = 64
D: x^2 + (y+8)^2 = 0
ANSWER: C: x^2 + y^2 = 64
Question 1(b): [1 mark]
Which of the following equations represents a line that passes through the point (0,7) and is tangent to a circle at point (3,4)?
Answer type: Multiple choice type 1
A: y = \dfrac{3}{4}x + 7
B: y = -x+7
C: y = 7x + \dfrac{3}{4}
D: y= 7x -1
ANSWER: B: y = -x+7
Question 1(c): [1 mark]
Choose the correct description for the equation x^2 + y^2 = 25.
Answer type: Multiple choice type 1
A: Centre (0,0), Radius 50
B: Centre (0,0), Radius 10
C: Centre (0,0), Radius 12.5
D: Centre (0,0), Radius 5
ANSWER: D: Centre (0,0), Radius 5
Question 2:
Consider the following circle with centre at (0,0) which crosses the point (-4,0).

Question 2(a): [1 mark]
What is the diameter of this circle?
Answer type: Simple text answer
ANSWER: 8
Question 2(b): [2 marks]
Find the equation of this circle. Choose the correct answer.
Answer type: Multiple choice type 1
A: x^2 + y^2 = 64
B: x^2 + y^2 = 16
C: x^2 + y^2 = 8
D: x^2 + y^2 = 4
ANSWER: B: x^2 + y^2 = 16
WORKING:
x^2 + y^2 = r^2
r = 4
x^2 + y^2 = 16
Question 3:
Answer the following questions.
Question 3(a): [2 marks]
Determine the radius for the following circle in surd form: x^2 + y^2 = 32.
Choose the correct answer.
Answer type: Multiple choice type 1
A: 4 \sqrt{2}
B: 2 \sqrt{2}
C: \sqrt{2}
D: 8 \sqrt{2}
ANSWER: A: 4 \sqrt{2}
WORKING:
Radius = \sqrt{32} = 4 \sqrt{2}
Question 3(b): [2 marks]
If the centre of the circle was moved 3 places to the left and 5 places up, what would the origin be?
Answer type: Multiple choice type 1
A: (-3,5)
B: (3,5)
C: (3,-5)
D: (-3,-5)
ANSWER: A: (-3,5)
WORKING:
Original centre was (0,0).
Question 4: [2 marks]
Consider the following circle, with centre (0,0).
Point P has the coordinates (-3,-5).
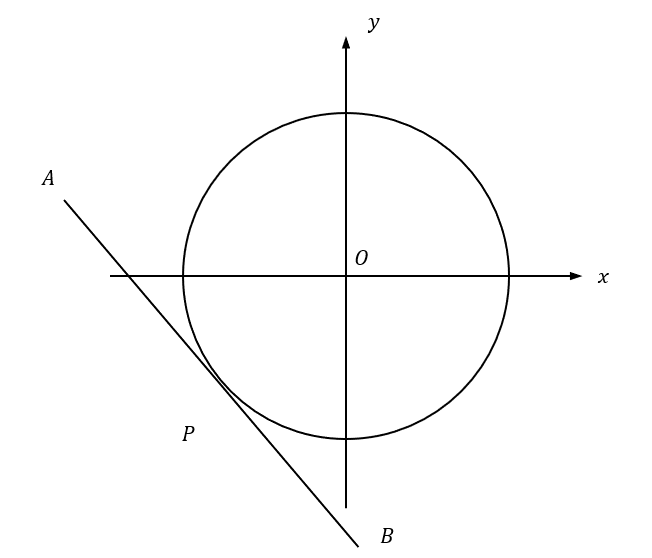
Work out the equation of the tangent, AB, to the circle at point P.
Choose the correct answer.
Answer type: Multiple choice type 1
A: 5y = -3x - 34
B: y = -15x - 34
C: 5y = -3x - 16
D: y = -15x - 16
ANSWER: A: 5y = -3x - 34
WORKING:
Equation of the line for the radius, through (-3,-5) is y = \dfrac{5}{3} x.
Slope of the tangent is - \dfrac{3}{5}.
y = - \dfrac{3}{5} x + c.
y-intercept:
-5 = - \dfrac{3}{5} (-3) + c
c = - 5 - \dfrac{9}{5} = \dfrac{34}{5}
y = - \dfrac{3}{5} x - \dfrac{34}{5}
5y = -3x - 34
Question 5: [2 marks]
Consider the following circle, with centre (0,0) and radius of 5.
Point P has the coordinates (-3,4).

Work out the equation of the tangent, AB, to the circle at point P.
Choose the correct answer.
Answer type: Multiple choice type 1
A: 4y = 3x + 25
B: 4y = 3x - 25
C: 3y = 4x + 25
D: 3y = 4x - 25
ANSWER: A: 4y = 3x + 25
WORKING:
Equation of the line for the radius, through (-3,4) is y = - \dfrac{4}{3} x.
Slope of tangent is \dfrac{3}{4}.
y = \dfrac{3}{4}x + c
y-intercept:
4 = \dfrac{3}{4}(-3) + c
c = 4 + \dfrac{9}{4} = \dfrac{25}{4}
y = \dfrac{3}{4}x + \dfrac{25}{4}
4y = 3x + 25
Question 6: [2 marks]
Consider the following circle, with centre (0,0) and a radius of 12.
Point Q has the coordinates (5,13).

Work out the equation of the tangent, AB, to the circle at point Q.
Choose the correct answer.
Answer type: Multiple choice type 1
A: 13y = -5x + 194
B: 5y = -13x + 194
C: 13y = 5x - 194
D: 5y = -13x - 194
ANSWER: A: 13y = -5x + 194
WORKING:
Equation of the line for the radius through (5,13) is y = \dfrac{13}{5} x
Slope of tangent is - \dfrac{5}{13}
y = - \dfrac{5}{13} x + c
y-intercept:
13 = - \dfrac{5}{13}(5) + c
c = 13 + \dfrac{25}{13} = \dfrac{194}{13}
y = - \dfrac{5}{13} x + \dfrac{194}{13}
13y = -5x + 194
Question 7: [2 marks]
Consider the following circle, with centre (-1,2), and a radius of 5.
Point P has coordinates (2,-2).
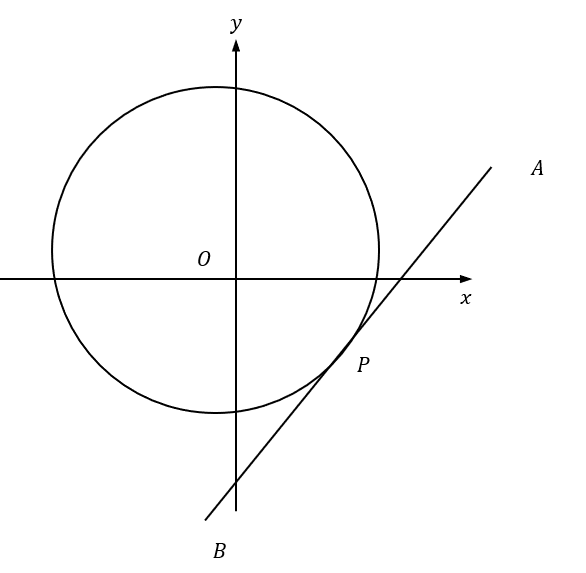
Work out the equation of the tangent, AB, to the circle at point P.
Choose the correct answer.
Answer type: Multiple choice type 1
A: 4y = 3x - 14
B: 3y = 4x - 14
C: 4y = 3x + 14
D: 3y = 4x + 14
ANSWER: A: 4y = 3x - 14
WORKING:
Equation of the line for the radius through (2,-2) is y = - \dfrac{4}{3} x.
Slope of tangent is \dfrac{3}{4}
y = \dfrac{3}{4}x + c
y-intercept:
-2 = \dfrac{3}{4}(2) + c
c = -2 - \dfrac{3}{2} = -\dfrac{7}{2}
y = \dfrac{3}{4}x -\dfrac{7}{2}
y = \dfrac{3}{4}x -\dfrac{7}{2}
Question 8: [2 marks]
Find the equation of a circle, with centre (0,0), where the tangent meets the circle at \bigg( \dfrac{12}{5}, - \dfrac{4}{5} \bigg).
Choose the correct answer.
Answer type: Multiple choice type 1
A: x^2 + y^2 = 6.4
B: x^2 + y^2 = 5.8
C: x^2 + y^2 = 5.4
D x^2 + y^2 = 6
ANSWER: A: x^2 + y^2 = 6.4
WORKING:
Given the centre of the circle is (0,0), by Pythagoras’ theorem, the radius is c, from
a^2 + b^2 = c^2
\bigg( \dfrac{12}{5} \bigg)^2 + \bigg( - \dfrac{4}{5} \bigg)^2 = c^2
c^2 = 6.4
c = \sqrt{6.4}
x^2 + y^2 = 6.4
