Question 1
1(a):
How long would it take you to travel 3 kilometres, if you walked at 6 km/h?
Give your answer in minutes.
ANSWER: Simple Text Answer
Answer: 30
Workings:
Using the equation: \text{Time} = \dfrac{\text{Distance}}{\text{Speed}} gives
Time = \dfrac{3}{6}=\dfrac{1}{2} hours = 30 minutes
Marks = 1
1(b):
What is Laura’s average speed in mph if she travels 126 miles in 2 hours?
ANSWER: Simple Text Answer
Answer: 63
Workings:
\text{Speed} = \dfrac{\text{Distance}}{\text{Time}}
\text{Speed} = \dfrac{126}{2}=63 mph
Marks = 1
1(c):
Emma travels at a speed of 23 miles per hour for 3.5 hours.
How far has she travelled in miles?
ANSWER: Simple Text Answer
Answer: 80.5
Workings:
\text{Distance} = \text{Speed} \times \text{Time}
\text{Distance} = 23 \times 3.5= 80.5 miles
Marks = 1
Question 2
2(a):
A car journey of 214 miles took Jack a total 7 hours and 15 minutes to complete.
Calculate his average speed across the journey to 2 decimal places.
ANSWER: Multiple Choice (Type 1)
A: 43.01 km/h
B: 29.52 mph
C: 33.43 mph
D: 45.38 km/h
Answer: B
Workings:
\text{Speed} = \dfrac{\text{Distance}}{\text{Time}} = \dfrac{214}{7.25} = 29.52 mph
Marks = 2
2(b):
Jack completed the return journey in half the time.
What was his average speed in mph on the return journey to 2 dp?
ANSWER: Multiple Choice (Type 1)
A: 59.03 mph
B: 54.55 km/h
C: 68.17 km/h
D: 64.19 mph
Answer: A
Workings:
\text{Time} = 3.625 hours
\text{Speed} = \dfrac{\text{Distance}}{\text{Time}} = \dfrac{214}{3.625} = 59.03 mph
Marks = 2
Question 3
3(a):
Nabeel travelled to London by train, her journey was made up of two parts.
One train into York and then another train into London.
The first train departed at 07:05 and the journey lasted for 12 minutes.
The second train departed at 07:27 and the journey lasted for 122 minutes.
The total distance travelled was 197 miles.
What was Nabeela’s average speed for the entire journey in mph to 2 dp?
ANSWER: Simple Text Answer
Answer: 82.08
Workings:
The length of the journey = 12+10+122 = 144 minutes = 2.4 hours
\text{Speed} = \dfrac{\text{Distance}}{\text{Time}} = \dfrac{197}{2.4} = 82.08 mph
Marks = 2
3(b):
York to London is a distance of 175 miles.
How many miles an hour faster was the first part of the journey to 2 dp?
ANSWER: Simple Task Answer
Answer: 23.93
Workings:
It took 12 minutes to travel 22 miles on the first train.
12 minutes = 0.2 hours
\text{Speed} = \dfrac{\text{Distance}}{\text{Time}} = \dfrac{22}{0.2} = 110 mph
The second train takes 122 minutes = 2.03 hours
\text{Speed} = \dfrac{175}{2.03} = 86.07 mph
To get the difference: Subtract the smaller speed from the bigger one.
110-86.07 = 23.93 mph difference
Marks = 3
Question 4
Trihao is driving from Cambridge to London.
Assume the distance between Cambridge and London is 100 km.
4(a):
Given that Trihao drives at an average speed of 80 km/h, work out his journey time.
ANSWER: Multiple Choice (Type 1)
A: 1 hour 6 minutes
B: 1 hour 57 minutes
C: 1 hour 15 minutes
D: 2 hours 28 minutes
Answer: C
Workings:
\text{Time} = \dfrac{\text{Distance}}{\text{Speed}} = \dfrac{100}{80} = 1.25 hours = 1 hour 15 minutes
Marks = 2
4(b):
Chris instead decides to take the train.
He leaves Cambridge at the same time as Trihao, but arrives in London 20 minutes before Trihao arrives.
Calculate the average speed of the train in km/h to the nearest integer.
ANSWER: Simple Text Answer
Answer: 109
Workings:
\text{Time} = 55 minutes = 0.917 hours
\text{Speed} = \dfrac{\text{Distance}}{\text{Time}} = \dfrac{100}{0.917} = 109
Marks = 2
Question 5
5(a):
Jordan finishes college at 16:30 h.
He walks to the his mum’s work 0.24 km away, at a speed of 2 km/h.
He waits there 7 minutes for his mum to finish work before she drives them both 7 km back home at an average speed of 26 km/h.
What time does Jordan arrive home?
Give your answer to the nearest minute.
ANSWER: Multiple Choice (Type 1)
A: 17:00
B: 17:07
C: 17:11
D: 17:12
Answer: A
Workings:
For the walking part of the journey
\text{Time} = \dfrac{\text{Distance}}{\text{Speed}} = \dfrac{0.24}{2} = 0.12 hours = 7 minutes
For the driving part of the question
\text{Time} = \dfrac{\text{Distance}}{\text{Speed}} = \dfrac{7}{26} = 0.2692 hours = 16 minutes
We can get the total journey time by adding the three parts together to get
7 + 7 + 16 = 30 minutes
Adding this to 16:30 gives an arrival time of 17:00
Marks = 3
5(b):
If Jordan jogs 7.1 km directly home at a speed of 7.4 km/h, at what time would he arrive home?
Give your answer to the nearest minute.
ANSWER: Multiple Choice (Type 1)
A: 17:17
B: 17:25
C: 17:28
D:17:35
Answer: C
Workings:
\text{Time} = \dfrac{\text{Distance}}{\text{Speed}} = \dfrac{7.1}{7.4} = 0.9595 hours = 57.5676 minutes
So Jordan would arrive home at 17:28
Marks = 2
Question 6
Anna needs to be at the museum for the open evening at 18.00 h.
She will walk to the museum from the bus depot at a speed of 3 mph.
To arrive at the bus depot she will catch the bus at the stop from near her house. The bus travels at an average speed of 25 mph.
On the walk from her house to the bus stop she will average a speed of 6mph.
The bus depot is 0.7 miles from the museum.
The bus journey from bus stop to bus depot is 2.2 miles.
The walk from her house to the bus stop is 0.3 miles.
Buses leave the bus stop at [/latex]15[/latex] minute intervals starting from 07:00 h.
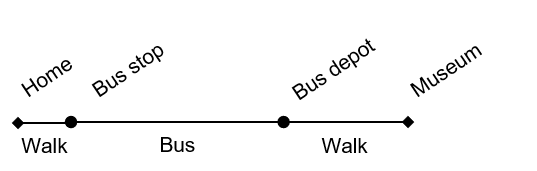
What is the latest bus Anna can catch and still arrive at the museum on time?
ANSWER: Multiple Choice (Type 1)
A: 17:45
B: 17:30
C: 17:15
D: 17:00
Answer: B
Workings:
To calculate the time for the walk from the depot to the museum:
\text{Time} = \dfrac{\text{Distance}}{\text{Speed}} = \dfrac{0.7}{3} = 0.23 hours = 14 minutes
To calculate the time for the bus journey:
\text{Time} = \dfrac{2.2}{25} = 0.088 hours = 5 minutes
To calculate the time or the walk from her house to the bus stop:
\text{Time} = \dfrac{0.3}{6} = 0.05 hours = 3 minutes
Adding the times together gives us a 22 minutes journey time
Subtracting this from 18:00 gives 17:38 but, because the buses go every 15 minutes, the last bus she can get is 17:30 to get her there before 18:00.
Marks = 4
Question 7
7(a):
Mrs Smith travels on Plane M, which flies at an average speed of 825 km/h for 7 hours and 24 minutes from Location A to Location B.
She then waits at Location B for 2 hours and 11 minutes, before flying to Location C on Plane N, which flies at an average speed of 722 km/h for 4 hours and 48 minutes.
Both planes fly in a straight line to their respective destinations.
What is the total distance of her journey in km to 1 dp?
ANSWER: Simple Text Answer
Answer: 9570.6
Workings:
Calculate the distance from A to B:
\text{Distance} = \text{Speed} \times \text{Time} = 825 \times 7.4 = 6105 km
Calculate the distance from B to C:
\text{Distance} = 722 \times 4.8 = 3465.6 km
Adding the two journeys together gives us a total distance travelled:
6105 + 3465.6 = 9570.6 km
Marks = 3
7(b):
The journey from Location A to Location B to Location C is such that it forms a right angle at Location B.
Plane Z flies directly from Location A to Location C at a speed of 795 km/h
If Plane Z leaves Location A at 11:53 h, what time does it arrive at Location C?
ANSWER: Multiple Choice (Type 1)
A: 20:22
B: 20:31
C: 20:37
D: 20:42
Answer: D
Workings:
Calculate the direct distance from A to C by using Pythagoras’ Theorem:
(AB)^2 + (BC)^2 = (AC)^2
AC = \sqrt{6105^2 + 3465.6^2} = 7020.1 km
\text{Time} = \dfrac{\text{Distance}}{\text{Speed}} = \dfrac{7020.0718}{795} = 8.8303 hours = 8 hours 50 minutes
Adding this onto 11:53 gives an arrival time of 20:43
Marks = 3
