01. Geometry Problems Foundation

Question 1

1(a):

Line $ADB$ is a straight line.

Find the angle $CDB$ shown below.

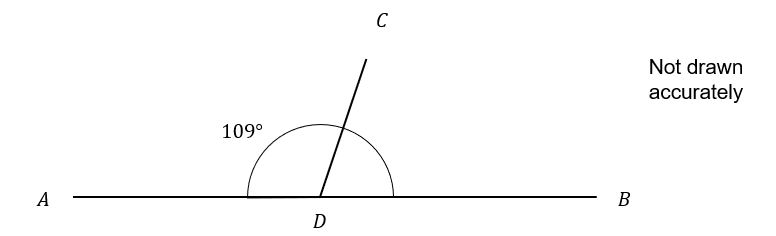
ANSWER: Multiple Choice (Type 1)

A: $41\degree$

B: $19\degree$

C: $71\degree$

D: $26\degree$

Answer: C

Workings:

Angles on a straight line add up to $180\degree$

We have two angles on the straight line, one of which is $109\degree$

So the other angle must be $180-109=71\degree$

Marks = 2

 

1(b):

$ABCD$ are points around a circle.

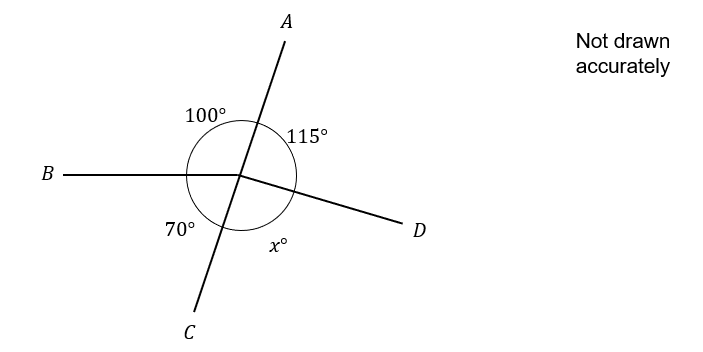
Find the value of $x$

ANSWER: Simple Text Answer

Answer: 75

Workings:

Angles around a point add up to $360\degree$

The existing angles added together gives $100+115+70=285$

We can find the missing angle by subtracting this from 360 to get $360-285=75$

Marks = 2

---

Question 2

$ACB$ forms a triangle shown below

$ABD$ is a straight line.

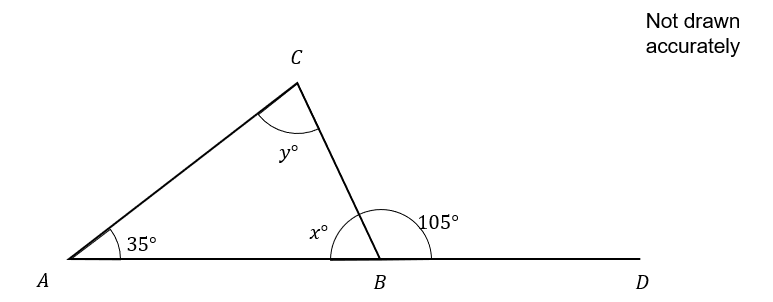
2(a):

Find angle $x$

ANSWER: Simple Text Answer

Answer: 75

Workings:

Angles on a straight line add up to $180\degree$

We can find the missing angle by subtracting the existing angle from 180 to get $180-105=75\degree$

Marks = 2

 

2(b):

Find angle $y$

ANSWER: Simple Text Answer

Answer: 70

Workings:

Angles in a triangle add up to $180$

We can subtract the existing angles from $180$ to get $180-35-75=70\degree$

Marks = 2

---

Question 3

$ACBD$ forms a quadrilateral shown below.

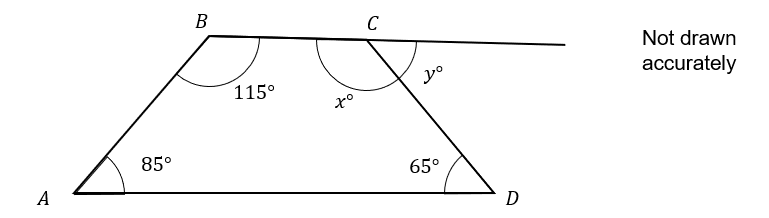
3(a):

Find $x$

ANSWER: Simple Text Answer

Answer: 95

Workings:

Angles in a quadrilateral add up to $360$.

We can subtract the quadrilateral’s existing angles from $360$ to find the missing angle.

This gives us $360-115-85-65=95\degree$.

Marks = 2

 

3(b):

Find $y$

ANSWER: Simple Text Answer

Answer: 85

Workings:

Angles on a straight line add up to $180$

To find the missing angle subtract the existing angle from $180$

This gives us $180-95=85\degree$

Marks = 2

---

Question 4

4(a):

$ABC$ forms an isosceles triangle shown below.

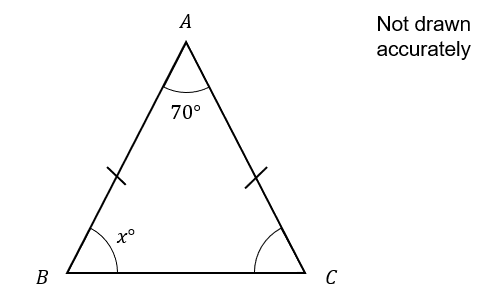
Find $x$

ANSWER: Simple Text Answer

Answer: 55

Workings:

Angles in a triangle add up to $180$

In an isosceles triangle the base angles are identical

We can subtract the given angle from $180$ and divide the result by $2$ to find the size of each.

$180-70=110$

$x=\dfrac{110}{2}=55\degree$

Marks = 2

 

4(b):

$EDF$ forms an isosceles triangle shown below.

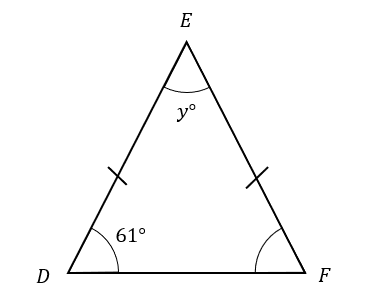
Find the value of $y$

ANSWER: Simple Text Answer

Answer: 58

Workings:

The base angles of an isosceles triangle are identical, so $F$ must also be $61\degree$

All angles in a triangle add up to $180\degree$

We can subtract the existing angles from $180$ to find $E$

$180-61-61=58\degree$

Marks = 2

---

Question 5

A compound shape is shown in the diagram below.

$ADEC$ forms a quadrilateral

$ABC$ is an isosceles triangle

$FAD$ is a straight line

Angle $CAD = x\degree$

Angle $BAC = y\degree$

Angle $ABC = z\degree$

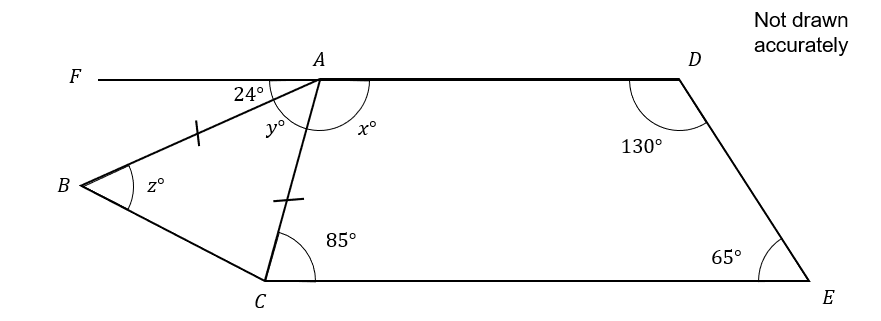
5(a):

Find $x$

ANSWER: Simple Text Answer

Answer: 80

Workings:

The angles of a quadrilateral add up to $360$

We can subtract the existing angles from $360$ to find the missing angle

$360-130-85-65=80\degree$

Marks = 2

 

5(b):

Find $y$

ANSWER: Simple Text Answer

Answer: 76

Workings:

Angles on a straight line add up to $180$

We can subtract the given angles from $180$ to find the missing angle

$180-24-80=76\degree$

Marks = 2

 

5(c):

Find $z$

ANSWER: Simple Text Answer

Answer: 52

Workings:

The base angles in an isosceles triangle are identical

The angles in a triangle add up to $180$

We can subtract the existing angle from $180$ and divide the result by $2$ to find $z$

$180-76=104$

$\dfrac{104}{2}=52\degree$

Marks = 2