Question 1
The two triangles below are congruent.
What is the value of y?

ANSWER: Multiple Choice (Type 1)
A: 40\degree
B: 50\degree
C: 60\degree
D: 70\degree
Answer: B
Workings:
Because the shape is congruent and has a right angle, both the other angles must be the same in each diagram.
The missing angle is 180-90-40=50\degree
Marks = 1
Question 2
Look at the shapes on the grid below.

2(a):
Which of these is a pair of congruent shapes
ANSWER: Multiple Choice (Type 1)
A: D & G
B: N & R
C: B & E
D: K & M
Answer: D
Workings:
K and M both have exactly the same side lengths and there are no other shapes with those dimensions.
Marks = 1
2(b):
Which of these is a triplet of congruent shapes
ANSWER: Multiple Choice (Type 1)
A: B, L & O
B: A, H & R
C: E, F & L
D: J, P & Q
Answer: A
Workings:
Shapes B, L & O all have the same side lengths
There are no other shapes with these dimensions
Marks = 1
Question 3
Below is a shape drawn on a centimetre grid.

3(a):
Which of the following diagrams shows the shape divided into four congruent shapes.
ANSWER: Multiple Choice (Type 1)
A:

B:

C:

D:

Answer: B
Workings:
Shape B is divided into 4 shapes of exactly the same size
This means the shapes are congruent
Marks = 1
3(b):
Dan believes that the shape can be divided into 8 congruent shapes.
Is he correct?
You must explain your answer
ANSWER: Multiple Choice (Type 1)
A: Yes, There are 4 lines of symmetry
B: Yes, There is enough space to make more shapes
C: No, There are only 2 lines of symmetry
D: No, The shape is too small
Answer: C
Workings:
To divide a shape into congruent shapes it must have at least one line of symmetry.
None of the congruent shapes found in part (a) have lines of symmetry so it is not possible to create any more congruent shapes.
Marks = 2
Question 4
ABC and XYZ are triangles
AB=XZ CB=XY \angle CBA= \angle ZXY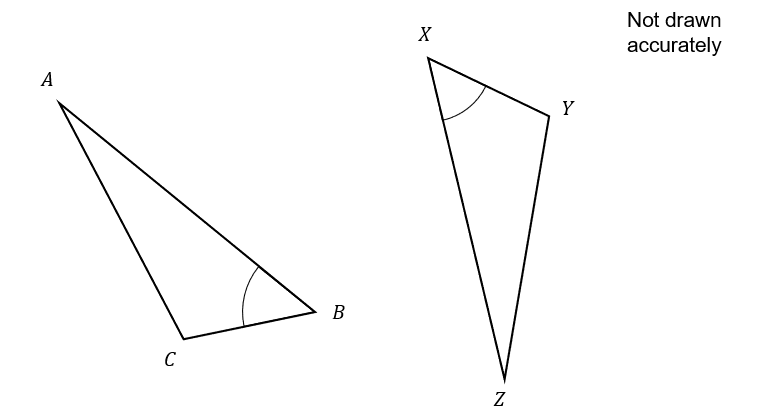
Which of the following conditions proves the triangles are congruent (using only information we know)
ANSWER:
A: The triangles have three sides of equal length
B: The triangles have two angles and a corresponding side that match up
C: The triangles have two sides and an angle between them that match up
D: The triangles have a right angle as well as the hypotenuse and one other side that all match up
Answer: C
Workings:
One of the conditions of congruence is that two identical side length with an identical angle between them.
This is true of these two triangles so they must be congruent.
Marks = 2
Question 5
Sophie draws a triangle with angles x, 4x and 7x.
Ben then uses this information to draw the triangle below.

5(a):
Is his triangle correct, based on the information given?
You must justify your answer.
ANSWER: Multiple Choice (Type 1)
A: Yes, We can work out that x = 15\degree
B: No, We can work out that x =20\degree
C: No, We can work out that x = 25\degree
D: No, We can work out that x = 30\degree
Answer: A
Workings:
Adding the angles together gives x + 4x + 7x =180
12x=180
x = 15
This matches the drawing given, so Ben is correct
Marks = 2
5(b):
Is Ben’s triangle congruent to Sophie’s?
You must explain your answer
ANSWER: Multiple Choice (Type 1)
A: Yes, because we know all the angles
B: Yes, because there is an equal difference between angle sizes
C: No, because none of the angles are equal
D: We don’t know, because we don’t know any of the side lengths
Answer: D
Workings:
In order to tell whether a triangle is congruent, we must know at least one of the side lengths in order for it to meet one of the congruence conditions.
Because we don’t have any side lengths it is not possible for us to tell from the angles alone whether the triangles are congruent.
Marks = 1
Question 6
In the diagram below:
\angle GFE = \angle EGFAB is parallel and equal to DC
E is the midpoint of BC
FA : AE = 1 : 3 GD : DE = 1 : 3
Using RHS, show that the triangles ABE and ECD are congruent.
ANSWER: Multiple Choice (Type 1)
A: BE = EC, \angle ABC=\angle DCE=90°, DE = AE
B: BE = DC, \angle ABC= \angleDCE=90°, DE = CE
C: BE = ED, \angle ABC=\angle CDE=90°, DE = AE
D: BE = ED, \angle ABC=\angle BEA=90°, DE = CE
Answer: A
Workings:
Using the given information, we know EFG is an isosceles triangle, so EF and EG are equal length
Given the ratios, we can therefore deduce AE = DE
We already know that AB = DC
E is the midpoint of BC so BE = CE
Because the sides on each triangle match each other we know the triangles must be congruent
Marks = 2
Question 7
Of the following, which can be used to prove two triangles are congruent?
AAA
AAS
SAS
RHS
SSS
SSA
ASA
ANSWER: Multiple Choice (Type 1)
A: AAA, AAS, RHS, ASA
B: AAS, RHS, SSA, ASA
C: AAS, RHS, SSS, ASA
D: AAS, SAS, RHS, SSS
Answer: D
Workings:
The four conditions that can prove that two triangles are congruent are:
ASA: Two angles and the side between them match up
AAS: Two angles and a corresponding side match up
SAS: Two sides and an angle between them match up
RHS: A right angle, the hypotenuse and one other side all match up
SSS: three sides are the same
Marks = 3
