Question 1
A delivery company uses two mathematically similar cardboard boxes.
The height of the smaller cuboid box is x.
The volume of the larger box is 8 times that of the smaller box.
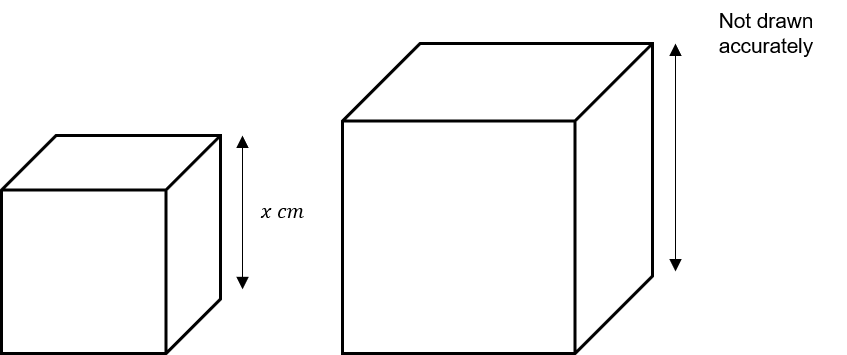
Find the height of the larger box.
Give your answer in terms of x.
ANSWER: Simple Text Answer
Answer: 2x
Workings:
The ratio of scale factors for lengths, SF_L, and for volumes, SF_V, is
SF_V = (SF_L)^3
Substituting in the volume of the larger box
8 = (SF_L)^3
Rearranging gives
SF_L = \sqrt[3]{8} = 2
So the height of the larger box must be 2x
Marks = 4
Question 2
Two mathematically similar wooden door wedges are shown below
The height of the smaller wedge is 6 cm and the width is 9 cm
The height of the larger wedge is 12 cm and the base is 16 cm
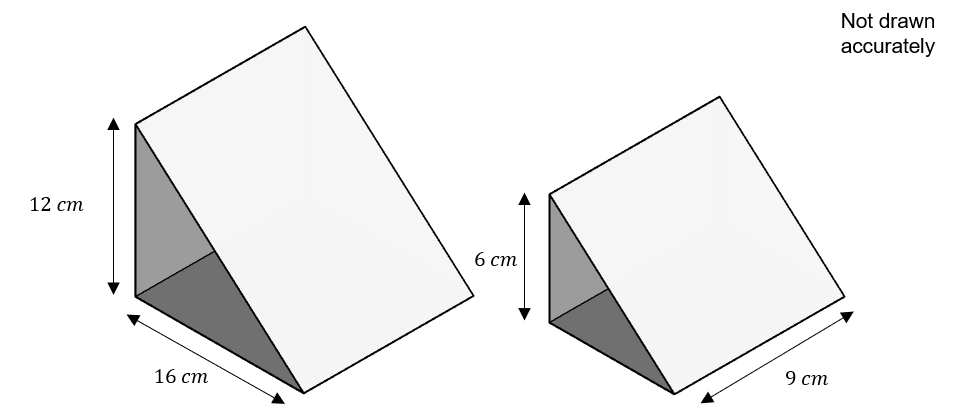
Find the volume of the smaller door wedge in cm^2.
ANSWER: Simple Text Answer
Answer: 216
Workings:
Using the heights of the two wedges to find the scale factor of side lengths
\dfrac{12}{6} = 2
Use this to find the length of the base of the smaller wedge
\dfrac{16}{2} = 8 cm
Calculate the area of the triangular side of the smaller wedge
\dfrac{1}{2}\times 8\times 6 = 24 cm^2
Multiply this area by the width of the smaller wedge to find its volume
24\times 9 = 216 cm^3
Marks = 3
Question 3
The diagram below shows a solid shape, with a section cut from the centre.
This section is mathematically similar to the original solid.
The scale factor of the larger shape to the smaller shape is 0.5
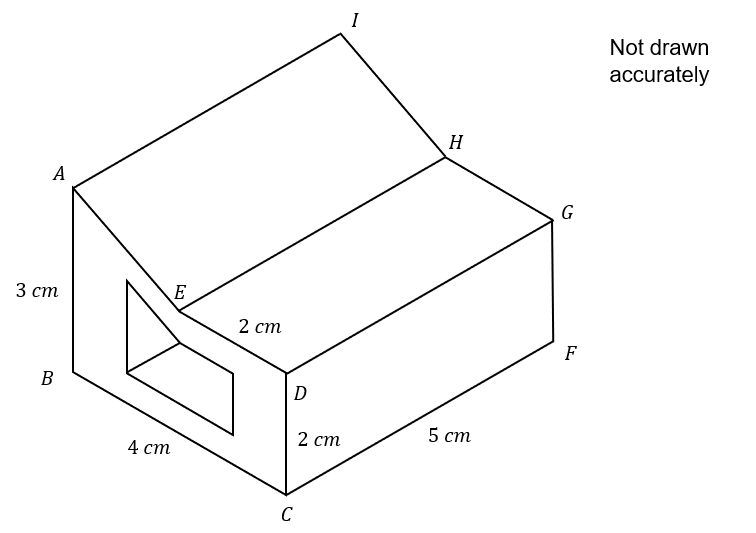
Calculate the volume of the shape shown above.
Give your answer to 3 significant figures in cm^3.
ANSWER: Simple Text Answer
Answer: 39.4
Workings:
The volume of the shape can be calculate as the volume of a trapezium prism and cuboid added together
\dfrac{1}{2}(2+3)\times (4-2) \times 5 + 2\times 2\times 5 = 25 + 20 = 45 cm^3
The scale factor for side lengths is 0.5
The scale factor for volume can be calculated as
0.5^3 = 0.125
This can be used to find the volume of the cut out area
0.125\times 45 = 5.625 cm^3
The total volume is found by subtracting the cut out shape from the larger shape
45 - 5.625 = 39.4 cm^3 (3 s.f.)
Marks = 5
Question 4
Two mathematically similar spheres are shown below.
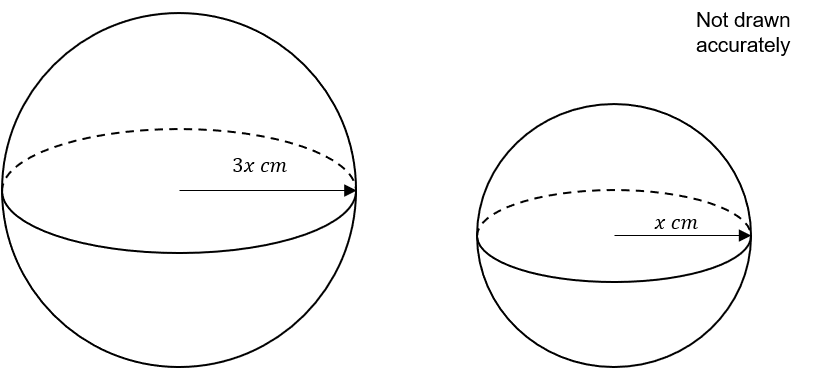
Work out the ratio of the surface area of the two similar spheres shown below.
Give your answer in its simplest form.
ANSWER: Multiple Choice (Type 1)
A: 9 : 1
B: 10 : 1
C: 11 : 1
D: 12 : 1
Answer: A
Workings:
Substituting the radius lengths into the formula for area of a sphere: 4\pi r^2
Smaller Sphere = 4\pi \times x^2
Larger Sphere = 4\pi \times (3x)^2 = 4\pi \times 9x^2
The ratio for larger : smaller sphere surface area
4\pi \times 9x^2 : 4\pi \times x^2
This gives the ratio for surface area
9 : 1
Marks = 3
Question 5
Two mathematically similar ice cream cones are delivered to a shop.
The height of the smaller cone is \dfrac{3}{4} that of the larger cone, shown below.
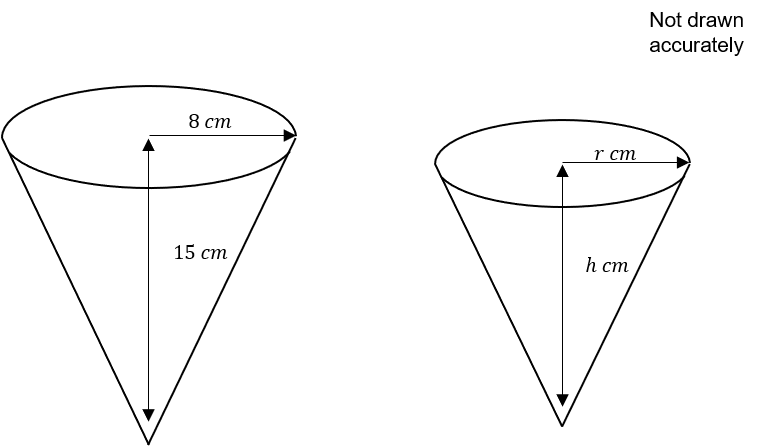
Work out the volume of the smaller cone.
Give your answer in terms of \pi.
ANSWER: Multiple Choice (Type 1)
A: 125\pi
B: 130\pi
C: 135\pi
D: 140\pi
Answer: C
Workings:
Volume of Cone = \dfrac{1}{3}\pi r^2h = \dfrac{1}{3}\pi \times 8^2 \times 15 = 320\pi
Scale Factor for cone volume can be found using
\dfrac{3}{4}^3 = \dfrac{27}{64}
Volume of smaller cone = \dfrac{27}{64}\times 320\pi = 135\pi
Marks = 4
Question 6
Two similar cylinders are shown below.
The height of the smaller cylinder is 10 cm and the height of the larger cylinder is 30 cm
Given the surface area of the smaller cone is 30π cm^2
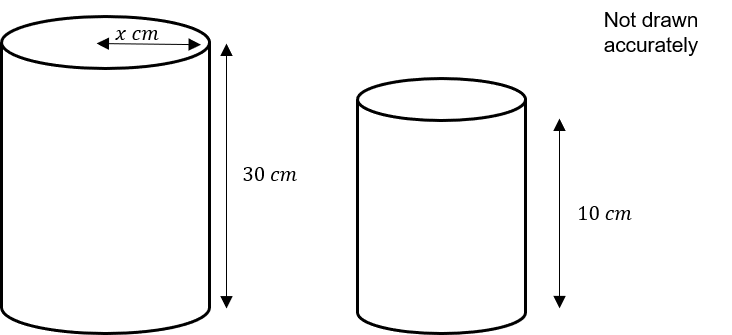
Find the radius of the larger cylinder.
Give your answer to 2 decimal places in cm.
Hint: surface area of a cylinder = 2\pi rh+2πr^2
ANSWER: Simple Text Answer
Answer: 3.97
Workings:
Using the cylinder heights, the scale factor must be \dfrac{1}{3}
The scale factor of the surface area can be found using
\dfrac{1}{3}^2 = \dfrac{1}{9}
The surface area of the larger cylinder can therefore be found using
9\times 30\pi = 270\pi cm^2
Use the formula for surface area of a cylinder: 2\pi r^2 + 2\pi rh
2\pi r^2 + 2\pi \times 30r = 270\pi
This cancels to get
r^2 + 30r - 135 = 0
Use quadratic formula
r = \dfrac{-30\pm \sqrt{1440}}{2} = 3.97 cm (2 d.p.)
Marks = 4
