Question 1
1(a):
Translate the shape R by the vector
\begin{pmatrix}-7\\-2\end{pmatrix}
ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: D
Workings:
The top left corner of Shape R has coordinates (2,5).
A translation by the vector \begin{pmatrix}-7\\-2\end{pmatrix} means the new shape will have coordinates
(2-7, 5-2) = (-5, 3)
This is given by Shape D
Marks = 2
1(b):
Translate the shape R by the vector
\begin{pmatrix}-3\\-5\end{pmatrix}
ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: C
Workings:
The top left corner of Shape R has coordinates (2,5)
A translation by the vector \begin{pmatrix}-3\\-5\end{pmatrix} means the new shape will have coordinates
(2-3, 5-5) = (-1,0)
This is given by Shape C
Marks = 2
1(c):
Describe the transformation that takes Shape A to Shape B

ANSWER: Multiple Choice (Type 1)
A: \begin{pmatrix}-3\\-3\end{pmatrix}
B: \begin{pmatrix}-6\\-6\end{pmatrix}
C: \begin{pmatrix}-1\\-1\end{pmatrix}
D: \begin{pmatrix}-4\\-4\end{pmatrix}
Answer: B
Workings:
Using the top left corner of both shapes
A has coordinates (2,5) and B has coordinates (-4,-1)
The translation can be found by subtracting the coordinates for A from the coordinates for B.
\begin{pmatrix}-4-2\\-1-5\end{pmatrix} = \begin{pmatrix}-6\\-6\end{pmatrix}
Marks = 2
Question 2
2(a):
Rotate the shape E by 180° clockwise about (0,0).
Which answer gives the transformed shape?

ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: C
Workings:
Using tracing paper, draw Shape E onto it and hold pencil onto point (0,0) while rotating the paper 180\degree
The new position of Shape E should now sit over the position of Shape C.
Marks = 2
2(b):
Rotate the shape E by 90° anticlockwise about (0,0).
Which answer gives the transformed shape?

ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: B
Workings:
Using tracing paper, draw Shape E onto it and hold pencil onto point (0,0) while rotating the paper 90\degree anticlockwise.
The new position of Shape E should now sit over the position of Shape B.
Marks = 2
Question 3
Which of the shapes A – D in the diagram below gives an incorrect reflection in the horizontal line of reflection?

ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: C
Workings:
Looking at the images below the reflection line, all of them are perfect reflections, except for Shape C which has been rotated around a point on the line of reflection instead.
Marks = 2
Question 4
4(a):
Which shape is a reflection of Shape G in the line y = 3?

ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
Answer: B
Workings:
Because Shape G is reflected in the line y=3, the points on the line of reflection must be the same: (1,3) and (3,3).
Shape B is the shape that matches this condition.
Marks = 1
4(b):
Which shape is a reflection of Shape G in the line x=-1?

ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
Answer: A
Workings:
The points in Shape G are all the same distance from the line x=-1 to the left of it as the points in Shape G to the right of it.
Therefore Shape A must be a reflection of Shape G in the line x=-1.
Marks = 1
4(c):
Which shape is a reflection of Shape G in the line y = 4 - x?

ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
Answer: A
Workings:
The line y=4-x passes through the point (1,3) on Shape A.
Because of this, a reflection in the line would mean the new shape also had a point at (1,3) (an invariant point).
This means Shape A must be the new shape.
Marks = 1
Question 5
Which shape is an enlargement of Shape Q by scale factor 0.5 with centre of enlargement (1,1)?

ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
Answer: B
Workings:
Draw ray lines onto the image, starting from point (1,1) and extending across the graph, passing through the points (5,7) and (7,4) on Shape Q.
The difference between points (1,1) and (5,7) is (5-1, 7-1) = (4,6).
The scale factor is 0.5 giving a difference between the new point and (1,1) of (2,3).
Adding this to point (1,1) will give the new point as (3,4).
Doing the same for the point (5,4) on Shape Q gives a difference between that point and (1,1) of (4,3).
Using the scale factor of 0.5, the new difference will be (2,1.5).
Adding to (1,1) will give the new point as (3,2.5).
These new points match Shape B in the diagram which must be the enlarged shape.
Marks = 3
Question 6
Each shape below has undergone a single transformation, starting from shape L.
Describe fully each transformation.

6(a):
From shape L to shape M:
ANSWER: Multiple Choice (Type 1)
A: Reflection in line y=0
B: Reflection in line y=3
C: Rotation 180\degree around point (0,0)
D: Reflection in line x=0
Answer: D
Workings:
Shape M is the same distance from the line x=0 as Shape L and has been flipped horizontally.
It is therefore a reflection of L in x=0.
Marks = 1
6(b):
From shape L to shape N:
ANSWER: Multiple Choice (Type 1)
A: Translation \begin{pmatrix}-6\\-4\end{pmatrix}
B: Translation \begin{pmatrix}-4\\-1\end{pmatrix}
C: Translation \begin{pmatrix}4\\-6\end{pmatrix}
D: Translation \begin{pmatrix}-2\\-1\end{pmatrix}
Answer: A
Workings:
The Shape L has moved 6 places to the left and 4 places down to reach Shape N.
This is a translation of \begin{pmatrix}-6\\-4\end{pmatrix}
Marks = 1
6(c):
From Shape L to Shape P:
ANSWER: Multiple Choice (Type 1)
A: Rotation 180\degree around the point (1,-1)
B: Reflection in the line y=-2x
C: Translation \begin{pmatrix}-4\\-6\end{pmatrix}
D: Reflection in the line y=-x
Answer: A
Workings:
The midpoint between the bottom left corner of Shape L and the top right corner of Shape P is (1,-1).
Using tracing paper, draw Shape L onto it and hold the pencil on point (1,-1).
Rotate the paper 180\degree to see that the shape on the tracing paper now sits above Shape P.
Therefore the transformation from Shape L to P is a rotation of 180\degree around the point (1,-1).
Marks = 1
6(d):
From Shape L to Shape Q:
ANSWER: Multiple Choice (Type 1)
A: Reflection in the line x=3
B: Rotation 180\degree around the point (3,-0.5)
C: Reflection in the line y=-0.5
D: Translation \begin{pmatrix}0\\-5\end{pmatrix}
Answer: B
Workings:
The midpoint between the bottom left corner of Shape L and the top right corner of Shape Q is (3,-0.5).
Using tracing paper, draw Shape L onto it and hold the pencil on point (3,-0.5).
Rotate the paper 180\degree to see that the shape on the tracing paper now sits above Shape Q.
Therefore the transformation from Shape L to Q is a rotation of 180\degree around the point (3,-0.5).
Marks = 1
7(e):
From Shape L to Shape R:
ANSWER: Multiple Choice (Type 1)
A: Rotation 180\degree around the point (3,1)
B: Translation \begin{pmatrix}1\\-1\end{pmatrix}
C: Rotation 180\degree around the point (4,2)
D: Reflection in the line y=x-2
Answer: D
Workings:
Adding a line y=x-2 to the graph shows that both shapes L and R have two points that sit on the line (invariant points).
Each point in Shape L is the same distance from y=x-2 as the corresponding point in Shape R.
Therefore Shape R must be a reflection of Shape L in the line y=x-2.
Marks = 1
Question 7
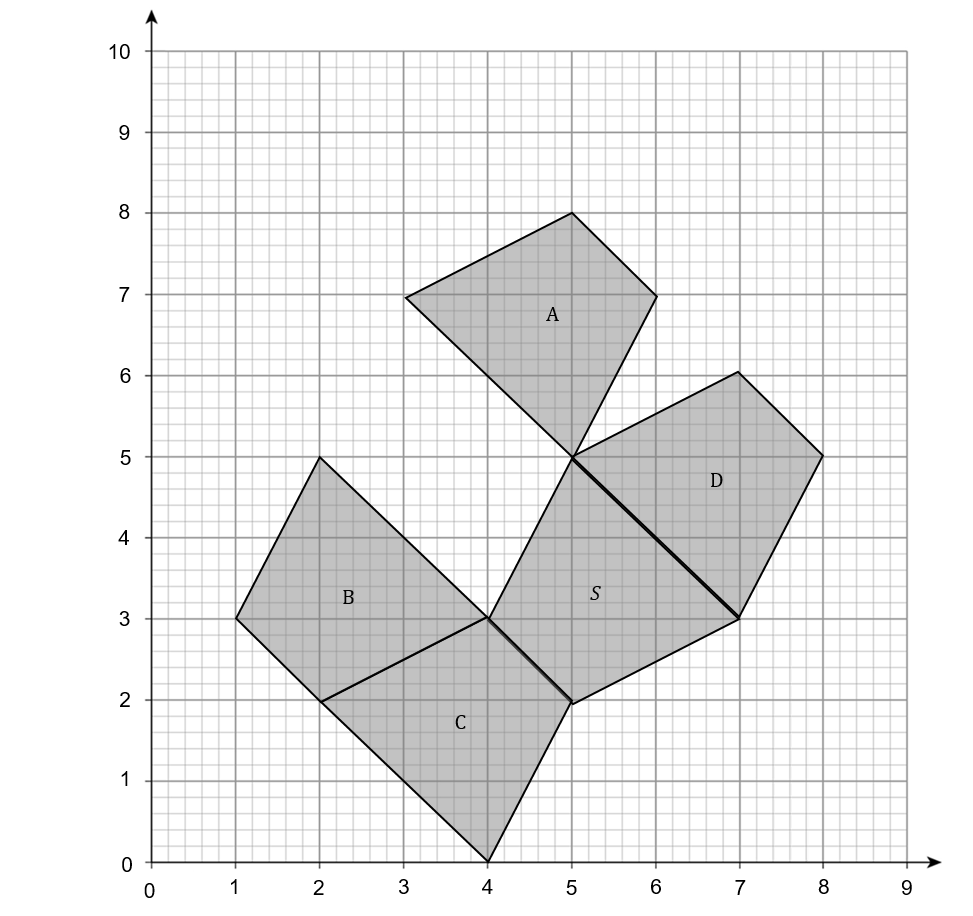
7(a):
Which shape gives a reflection of S in the line y=7-x?
ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: C
Workings:
Shape C is Shape S after being mirrored in the line y=7-x
Marks = 1
7(b):
Which shape gives a translation of Shape S by \begin{pmatrix}-3\\0\end{pmatrix}?
ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: B
Workings:
Moving Shape S three units to the left leaves it in the position of Shape B.
Marks = 1
7(c):
Which shape gives a rotation of Shape S by 180\degree around point (5,5)?
ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: A
Workings:
Using tracing paper, draw Shape S onto it. Hold the pencil at point (5,5) and rotate the paper 180\degree.
The shape is now in the position of Shape A.
Marks = 2
Question 8
8(a):
Which shape shows P enlarged by scale factor 2.5 with centre of enlargement (-7,5)?

ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: D
Workings:
Draw two ray lines from the point (-7,5); one passing through the point (-3,7) on Shape P and the other passing through point (-3,4) on the
same shape.
To get from point (-7,5) to (-3,7) there is an increase of 4 horizontally and 2 vertically.
Because the scale factor is 2.5, the new point will be a horizontal distance of 10 from the centre of enlargement and a vertical distance of 5.
This means the new point must be at (-7+10, 5+5) = (3,10)
To get from point (-7,5) to (-3,4) there is an increase of 4 horizontally and -1 vertically.
Because the scale factor is 2.5, the new point will be a horizontal distance of 10 from the centre of enlargement and a vertical distance of -2.5.
This means the new point must be at (-7+10, 5-2.5) = (3,2.5)
Therefore the new shape that matches these points must be Shape D.
Marks= 2
8(b):
Which shape shows P enlarged by scale factor 1.5 with centre of enlargement (-7,9)?

ANSWER: Multiple Choice (Type 1)
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: C
Workings:
Draw two ray lines from the point (-7,9); one passing through the point (-3,7) on Shape P and the other passing through point (-3,4) on the same shape.
To get from point (-7,9) to (-3,7) there is an increase of 4 horizontally and -2 vertically.
Because the scale factor is 1.5, the new point will be a horizontal distance of 6 from the centre of enlargement and a vertical distance of -3.
This means the new point must be at (-7+6, 9-3) = (-1,6)
To get from point (-7,9) to (-3,4) there is an increase of 4 horizontally and -5 vertically.
Because the scale factor is 1.5, the new point will be a horizontal distance of 6 from the centre of enlargement and a vertical distance of -7.5.
This means the new point must be at (-7+6, 9-7.5) = (-1,1.5)
Therefore the new shape that matches these points must be Shape C.
Marks = 2
8(c):
What centre of enlargement is used to enlarge Shape J to Shape K?

ANSWER: Multiple Choice (Type 1)
A: (-5,2)
B: (-8,3)
C: (-7,0)
D: (-4,2)
Answer: C
Workings:
Draw a line passing through the points (3,10) and (-1,6).
Draw another line, this one passing through the points (3,2.5) and (-1,1.5).
Where the two lines intersect gives us the centre of enlargement.
Marks = 2
