Question 1
The diagram below shows cuboid ABCDEFGH.
AB=3 cm
BC=12 cm
CF=16 cm
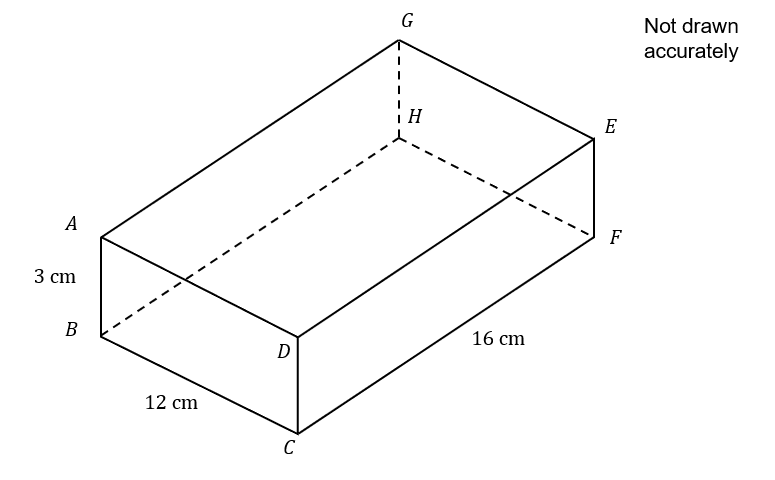
Calculate the total volume of the cuboid shown in cm^3.
ANSWER: Simple Text Answer
Answer: 576
Workings:
Calculate the area of the end face
3\times 12 = 36 cm^2
Multiply by the length to find the volume
36\times 16 = 576 cm^3
Answer: 1
Question 2
The diagram below shows a square based pyramid ABCDE.
The vertical height of the pyramid is 12 m
CD=5 m

Using the equation above, calculate the volume of the pyramid shown in m^3.
ANSWER: Simple Text Answer
Answer: 100
Workings:
Calculate the area of the base
5\times 5 = 25 m^2
Substitute into the equation for volume of a pyramid
\dfrac{25\times 12}{3} = 100 m^3
Marks = 2
Question 3
Two cuboids have been joined to make the shape below.
FG=7 cm
FC=3 cm
CA=4 cm
GH=2 cm
AB=4 cm
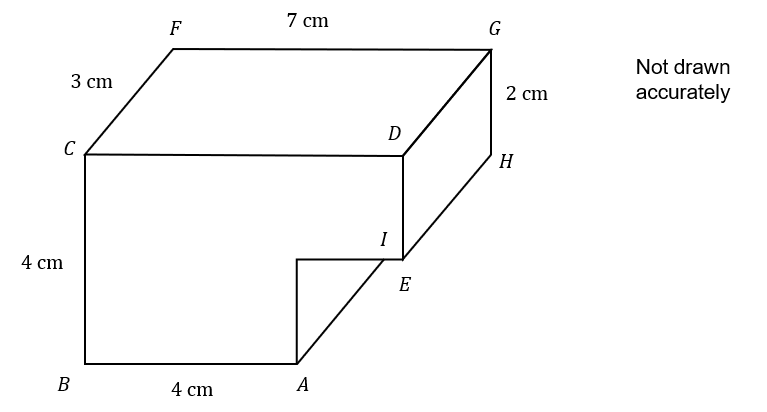
3(a):
Calculate the area of the face ABCDE in cm^2
ANSWER: Simple Text Answer
Answer: 22
Workings:
The shape ABCDE can be split into two shapes, one square with side length 4 cm and one rectangle with side lengths 3 cm and 2 cm.
The area of the square is 4\times 4 = 16 cm^2
The area of the rectangle is 3\times 2 = 6 cm^2
Adding these two areas together gives the the total area
16 + 6 = 22 cm^2
Marks = 2
3(b):
Calculate the total volume of the 3D shape shown above in cm^3.
ANSWER: Simple Text Answer
Answer: 66
Workings:
The volume of the shape is given by: area of the cross-section \times length
22\times 3 = 66 cm^3
Marks = 1
Question 4
The cylinder shown below has a diameter of 9 cm and height 2 cm.
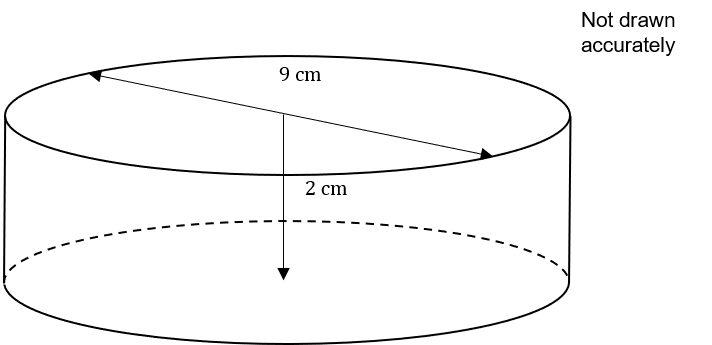
Calculate the volume of the cylinder shown above.
Give your answer to 2 decimal places in cm^3.
ANSWER: Simple Text Answer
Answer: 127.23
Workings:
Calculate the area of the circular face
\pi r^2 = \pi \times \dfrac{9}{2}^2 = \dfrac{81\pi}{4}
Multiply by the height to get the volume
\dfrac{81\pi}{4}\times 2 = \dfrac{81\pi}{2} = 127.23 cm^3
Marks = 2
Question 5
A sphere with radius 4 cm is shown below.
Volume of a sphere: V=\dfrac{4}{3}\pi r^3
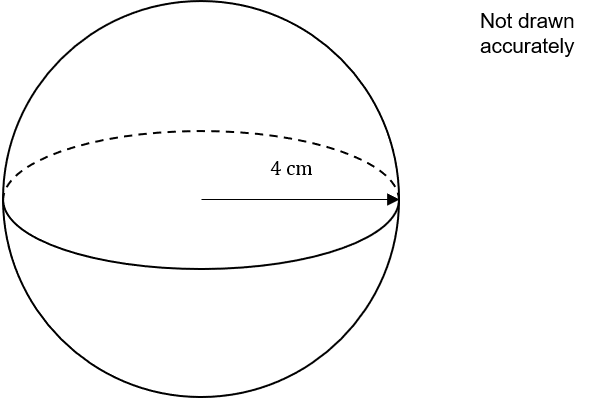
Calculate the volume of the sphere above.
Give your answer in terms of \pi
ANSWER: Multiple Choice (Type 1)
A: \dfrac{263\pi}{3}
B: \dfrac{250\pi}{3}
C: \dfrac{260\pi}{3}
D: \dfrac{256\pi}{3}
Answer: D
Workings:
Substitute the radius of the sphere into the equation for its volume
\dfrac{4}{3}\pi \times 4^3 = \dfrac{256\pi}{3}
Marks = 2
Question 6
1500 ml of water is poured into an open-topped cylinder with diameter 16 cm and height 12 cm.
1 ml=1 cm^3
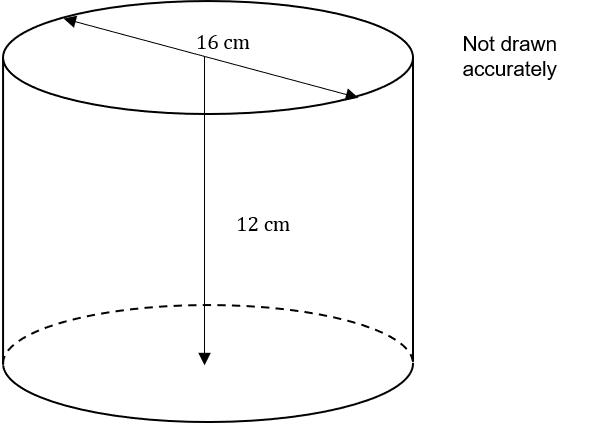
How high does the water reach from the base of the cylinder?
Give your answer to 2 decimal places in cm.
ANSWER: Simple Text Answer
Answer: 7.46
Workings:
Calculate the volume of the cylinder using the formula V = \pi r^2h
V = \pi \times \dfrac{16}{2}^2 \times 12 = 768\pi cm^3
Calculate the height of the water using
\dfrac{\text{volume of water}}{\text{volume of cylinder}}\times height of cylinder = \dfrac{1500}{768\pi}\times 12 = 7.46 cm
Marks = 3
Question 7
The diagram below shows an ice-cream cone.
This consists of a cone, of radius 3 cm and height 10 cm with an attached hemisphere of ice cream of radius 3 cm, as shown below.

Assuming the cone is completely filled, calculate the volume of Ice-cream held by the cone.
Give your answer in terms of \pi
ANSWER: Multiple Choice (Type 1)
A: 48\pi
B: 50\pi
C: 52\pi
D: 54\pi
Answer: A
Workings:
Volume of a cone is given by \dfrac{1}{3}\pi r^2h
Substituting in the given values gives the volume of the cone as \dfrac{1}{3}\times \pi \times 3^2 \times 10 = 30\pi cm^3
Calculate the volume of the hemisphere as {2}{3}\pi r^3
Substituting in the given values gives the volume of the hemisphere as \dfrac{2}{3}\times \pi \times 3^3 = 18\pi
Adding the two volumes together gives 30 + 18 = 48 cm^3
Marks = 4
Question 8
The diagram below shows a square based pyramid ABCDE.
The vertical height of the pyramid is 3h
Water fills the square based pyramid to a height of h.
The top of the water can be seen along line WXYZ.
AB=x\\ WX=\dfrac{1}{2}x
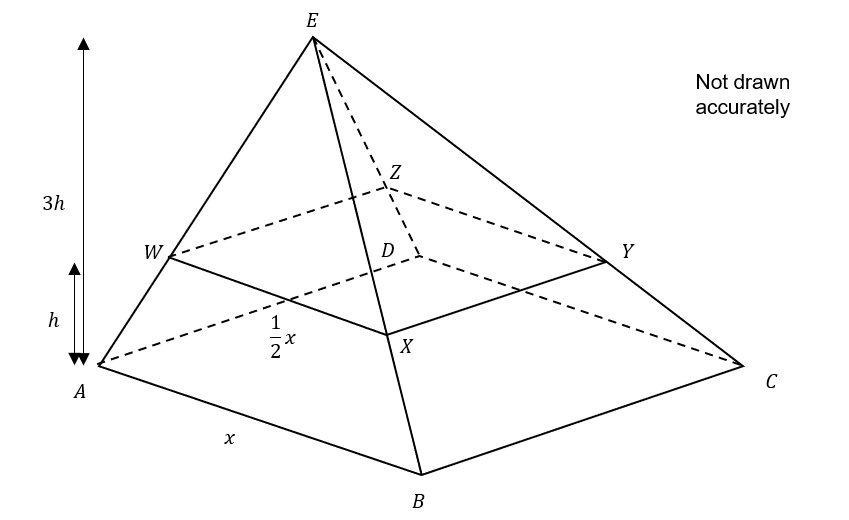
Calculate the proportion of the pyramid that is filled with water.
Give your answer as a fraction in its simplest form.
ANSWER: Multiple Choice (Type 1)
A: \dfrac{2}{7}
B: \dfrac{4}{5}
C: \dfrac{7}{10}
D: \dfrac{5}{6}
Answer: D
Workings:
Calculate the volume of the full pyramid
\dfrac{1}{3}\times x^2 \times 3h = hx^2
Calculate the volume of the smaller pyramid
\dfrac{1}{3}\times \dfrac{1}{4}x^2\times 2h = \dfrac{hx^2}{6}
Calculate the volume of the frustum by subtracting the small pyramid from the large pyramid
hx^2 - \dfrac{hx^2}{6} = \dfrac{5hx^2}{6}
Divide the volume of the frustum by the total volume of the pyramid to get the proportion filled with water
\dfrac{(\dfrac{5hx^2}{6})}{hx^2}=\dfrac{5}{6}
Marks = 4
