Question 1
A cone with a height of 35 cm has had part of the shape removed.
This has the left the frustum shown below.
The vertical height is 15 m
The radius of the base is 7 m
The top radius is 4 m
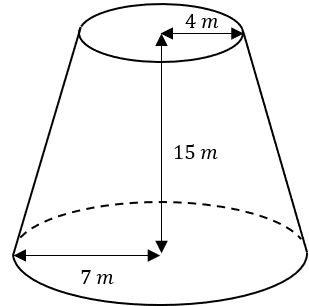
Calculate the volume of the frustum.
Give your answer to 2 decimal places in m^3.
ANSWER: Simple Text Answer
Answer: 1460.84
Workings:
Calculate the volume of the original cone using the formula V = \dfrac{1}{3}\pi r^2h
V = \dfrac{1}{3}\pi \times 7^2\times 35 = 1795.9438
Now calculate the volume of the top cone that has been removed
V = \dfrac{1}{3}\pi \times 4^2 \times 20 = 335.1032
Subtract the removed cone from the original cone to get the answer
1795.9438-335.1032 = 1460.84 m^3
Marks = 4
Question 2
A frustum is shown below.
The slanted height of the frustum 14 m
The slanted height of the original cone is 23.3. m
The radius of the base is 10 m
The top radius is 4 m
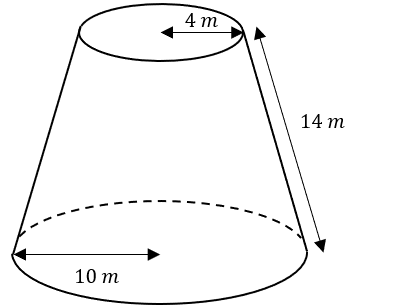
Calculate the surface area of the frustum above.
Give your answer to 2 decimal places.
ANSWER: Simple Text Answer
Answer: 979.55
Workings:
Calculate the surface area of the original cone
\pi r^2 + \pi rl = \pi \times 10^2 + \pi \times 10\times 23.3 = 333\pi
Calculate the area of the curved face of the removed cone
\pi \times 4\times 9.3 = \dfrac{186\pi}{5}
Calculate the area of the top circle on the frustum
\pi \times 4^2 = 16\pi
Add the area of the top frustum circle to the original surface area and subtract the area of the removed section
333\pi + 16\pi - \dfrac{186\pi}{5} = 979.55
Marks = 5
Question 3
A frustum is cut from a square based pyramid as shown below.
The height of the frustum is 7 m
The height of the pyramid on top of the frustum is 8.75 m
The large square base is 9 m wide.
The square top is 5 m wide.
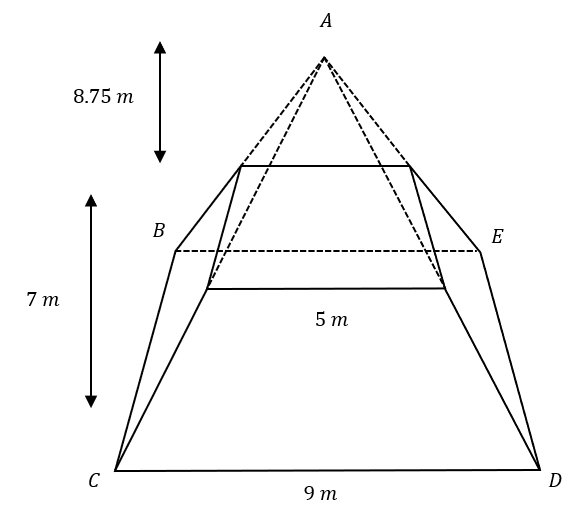
Calculate the volume of the frustum.
Give your answer to 2 decimal places.
ANSWER: Simple Task Answer
Answer: 352.33
Workings:
Calculate the volume of the full pyramid using V = \dfrac{1}{3}a^2h
V = \dfrac{1}{3}\times 9^2\times 15.75 = 425.25
Calculate the volume of the smaller pyramid
V = \dfrac{1}{3}\times 5^2\times 8.75 = 72.9167
Subtract the smaller pyramid from the full pyramid to get the volume of the frustum
425.25-72.9167 = 352.33 m^3
Marks = 3
Question 4
A section is cut from the top of a square-base pyramid of height 14 cm to create a frustum as shown below.
The base of the frustum has a width of 7 cm.
The top of the frustum has a width of 2 cm.
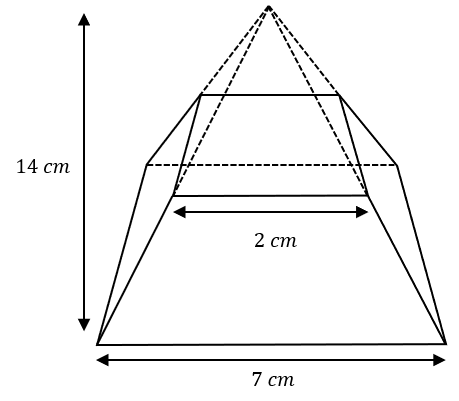
Calculate the exact volume of the frustum shown above.
ANSWER: Multiple Choice (Type 1)
A: \dfrac{580}{3} cm^3
B: \dfrac{610}{3} cm^3
C: \dfrac{640}{3} cm^3
D: \dfrac{670}{3} cm^3
Answer: D
Workings:
Calculate the volume of the full pyramid
\dfrac{1}{3}\times 7^2\times 14 = \dfrac{686}{3}
Calculate the volume of the smaller pyramid
\dfrac{1}{3}\times 2^2\times 4 = \dfrac{16}{3}
Calculate the volume of the frustum by subtracting the smaller pyramid from the full pyramid
\dfrac{686}{3}-\dfrac{16}{3} = \dfrac{670}{3}
Marks = 3
Question 5
A cone with radius 7 cm and height 10 cm, has a smaller cone of radius 3 cm, cut from its top.
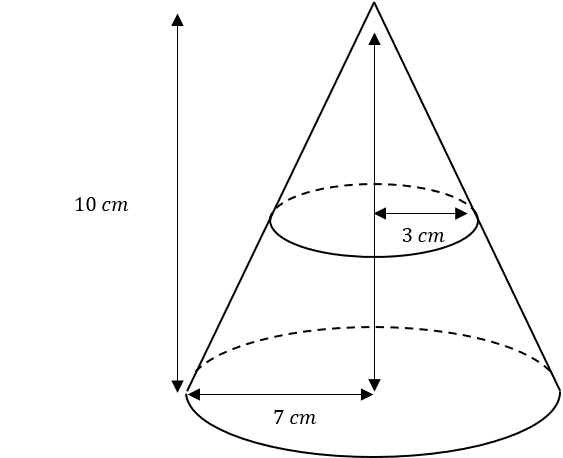
Find the height of the frustum after the smaller cone is removed.
Give your answer to 2 decimal places.
ANSWER: Simple Text Answer
Answer: 5.71
Workings:
Using ratios of bases, the height of the smaller cone is \dfrac{3}{7} of the bigger cone, \dfrac{30}{7} cm
Subtract the height of the smaller cone from the height of the bigger cone to find the height of the frustum
10-\dfrac{30}{7} = 5.71 cm
Marks = 3
Question 6
A cone has a radius of 12 m and a slanted height 15 m.
A smaller cone of radius 3 m is cut from its top.
x is the slanted height of the frustum remaining.
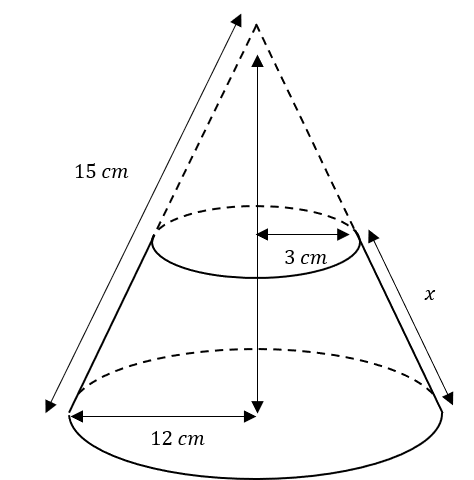
Find x
Give your answer to2 decimal places.
ANSWER: Simple Text Answer
Answer: 11.25
Workings:
Because the cones are mathematically similar the smaller cone is an enlargement of scale factor \dfrac{3}{12} = 0.25 of the big cone
This means the small cone has slanted height \dfrac{15}{4}=3.75 cm
The slanted side, x, of the frustum can be found as x=15-3.75=11.25 cm
Marks = 3
Question 7
A triangular pyramid is 20 cm tall.
The top is cut off leaving a 6 cm tall frustum.
The base of the pyramid is an equilateral triangle, with each length 11 cm.
The top of the frustum has a width of 7 cm.
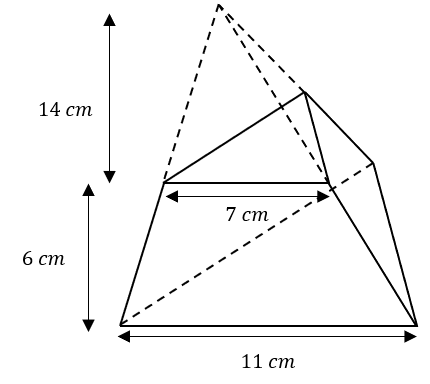
Calculate the volume of the 6 cm tall frustum to 2 decimal places in cm^3.
ANSWER: Simple Text Answer
Answer: 250.28
Workings:
Calculate the area of the base
\sqrt{11^2-5.5^2} = \dfrac{11\sqrt{3}}{2} gives the height of the triangle
\dfrac{1}{2}\times 11\times \dfrac{11\sqrt{3}}{2} = 52.3945 cm^2 gives the area
Calculate volume of full pyramid
\dfrac{1}{3}\times 52.3945\times 20 = 349.2967 cm^3
Calculate base area of small pyramid
\sqrt{7^2-3.5^2} = \dfrac{7\sqrt{3}}{2} gives height of the base
\dfrac{1}{2}\times 7\times \dfrac{7\sqrt{3}}{2} = \dfrac{49\sqrt{3}}{4} gives the area
Calculate volume of small pyramid
\dfrac{1}{3}\times \dfrac{49\sqrt{3}}{4}\times 14 = 99.0156 cm^3
Subtract the volume of the smaller pyramid from the volume of the large pyramid
349.2967-99.0156 = 250.28 cm^3
Marks = 4
