Question 1
In the diagram below, AB is parallel to line CD.
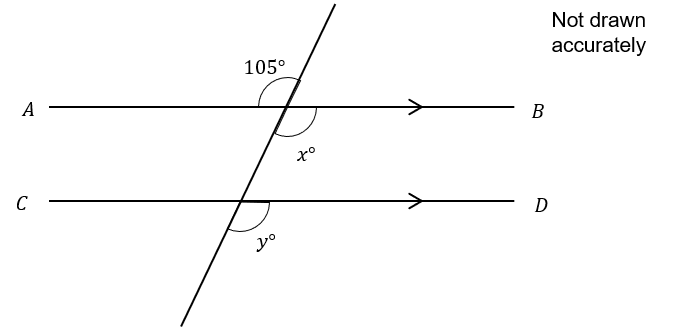
1(a):
Find the value of x
ANSWER: Simple Text Answer
Answer: 105
Workings:
Opposite angles at a point are equal
x=105\degree
Marks = 2
1(b):
Find the value of y
ANSWER: Simple Text Answer
Answer: 105
Workings:
Corresponding angles on parallel lines will always be the same. So x=y=105\degree
Marks = 2
Question 2
In the diagram below, AB is parallel to line CD.
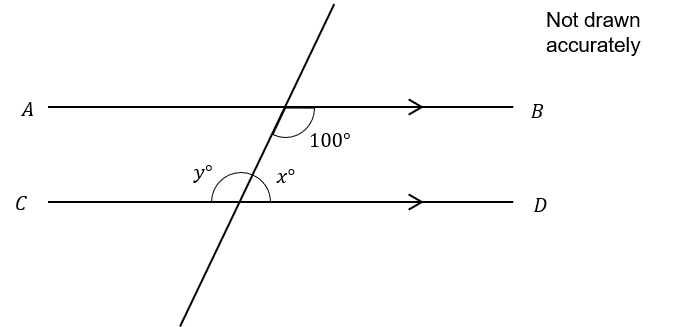
2(a):
Find the value of x
ANSWER: Simple Text Answer
Answer: 80
Workings:
Co-interior angles add up to 180
We can find the missing angle by subtracting the existing angle from 180
x=180-100=80\degree
Marks = 1
2(b):
Find the value of y
ANSWER: Simple Text Answer
Answer: 100
Workings:
Angles on a straight line add up to 180
We can find the missing angle by subtracting the existing angle from 180
y=180-80=100\degree
Marks = 2
Question 3
In the diagram below, AB is parallel to line CD.

Find the value of x
ANSWER: Simple Text Answer
Answer: 75
Workings:
Alternate angles are equal
Angles on a straight line add up to 180
We can find the missing angle by subtracting the existing angle from 180
x=180-105=75
Marks = 3
Question 4
In the diagram below, AB is parallel to line CD and EF.
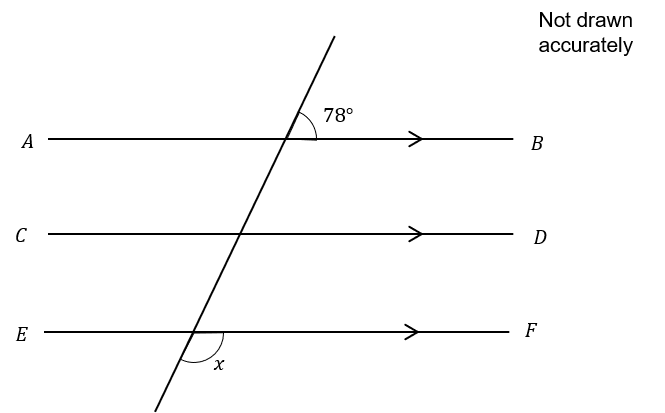
Find the value of x
ANSWER: Simple Text Answer
Answer: 102
Workings:
Angles on a straight line add up to 180 so the angle adjacent to 78 will be 102
All three lines AB, CD, EF are parallel
So x is a corresponding angle and x=102
Marks = 3
Question 5
ABC is an isosceles triangle shown below
Lines DE and BC are parallel
AB = AC
Find the value of x
ANSWER: Simple Text Answer
Answer: 40
Workings:
Corresponding angles are equal, so C = 40
Base angles of an isosceles triangle are equal, so x=40\degree
Marks = 3
Question 6
The diagram below shows two parallel lines and a rectangle
AB=FEBCED is a rectangle
Angle ABD=50°
Angle DEF=x°
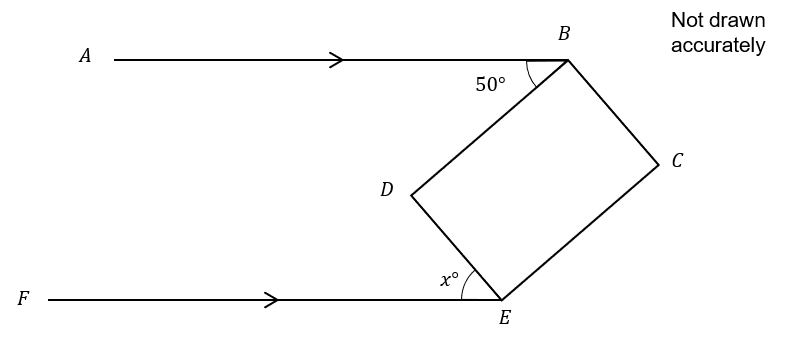
Find the value of x
ANSWER: Simple Text Answer
Answer:40
Workings:
Using exterior angles of a quadrilateral the two angles must equal 90\degree
x=90-50=40\degree
Marks = 2
