Question 1
1(a):
Which drawing gives the locus of all points that are 4 cm from the central point shown below?
ANSWER: Multiple Choice (Type 2)
A:

B:

C:

D:
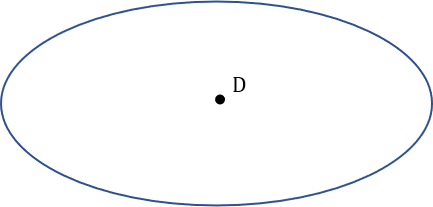
Answer: B
Workings:
All points on a circle are the same distance from the centre.
Marks = 1
1(b):
Which locus represents all points 2 away from the given line segment?
ANSWER: Multiple Choice (Type 2)
A:

B:
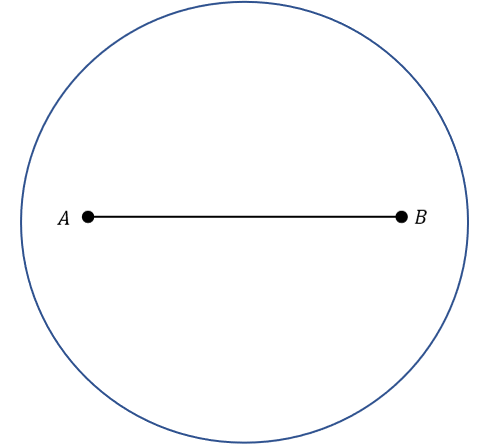
C:

D:
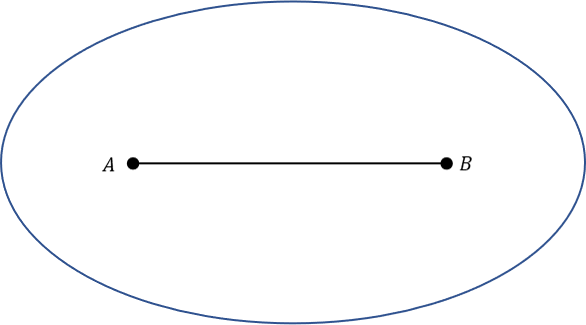
Answer: A
Workings:
To find the locus of points around either point A or point B, a circle would be drawn around the point.
The locus between A and B will consist of two parallel lines, both equidistant from AB.
Therefore the complete locus will consist of two parallel lines either side of AB, with a semi circle connecting the lines at both ends.
Marks = 2
Question 2
Which diagram shows the correct construction lines for finding the locus of all points equidistant from A and B?
ANSWER: Multiple Choice (Type 2)
A:

B:

C:
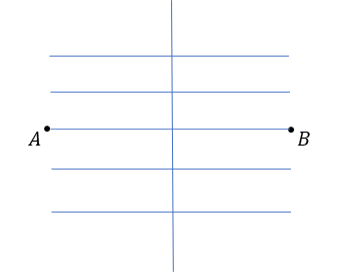
D:

Answer: A
Workings:
The locus of the points equidistant from A and B will be the line that perpendicularly bisects the line AB.
Using a compass, draw an arc around point A of radius at least \dfrac{1}{2}AB.
Keeping the compass the same length, draw a similar arc around point B.
Draw a line that passes through the points of intersection of the two arcs.
This is the required locus.
Marks = 2
Question 3
Which diagram shows the construction lines required to draw a perpendicular line that crosses the mid-point of AB?
ANSWER: Multiple Choice (Type 2)
A:
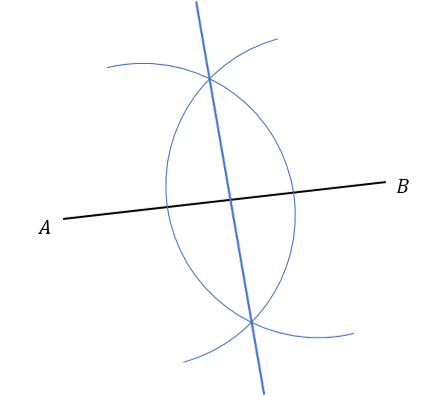
B:
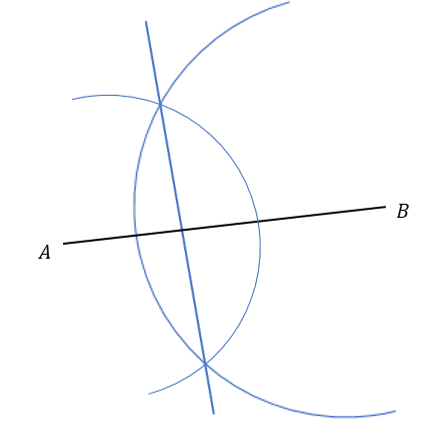
C:
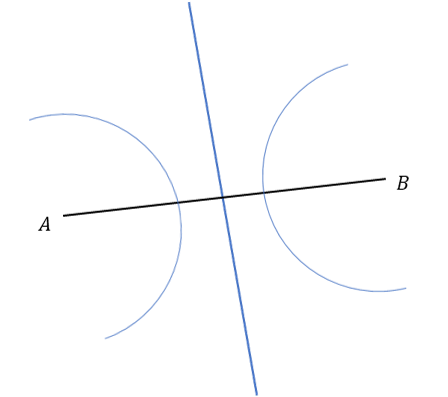
D:

Answer: A
Workings:
The perpendicular line that crosses the midpoint of AB is the same as the locus of all points equidistant from A and B.
Using a compass, draw an arc around point A of radius at least \dfrac{1}{2}AB.
Keeping the compass the same length, draw a similar arc around point B.
Draw a line that passes through the points of intersection of the two arcs.
This is perpendicular to the line AB and passes through its midpoint.
Marks = 2
Question 4
4(a):
Define the bisector of an angle.
ANSWER: Multiple Choice (Type 1)
A: The bisector of an angle is a line segment which divides the angle into two equal parts.
B: The bisector of an angle is a line segment that creates an angle of 180\degree with an existing line segment.
C: The bisector of an angle is a line segment that completes a triangle, where the other two sides make the original angle.
D: The bisector of an angle is a line segment that passes through the point where two line segments makes an angle, but doesn’t cross either line.
Answer: A
Marks = 1
4(b):
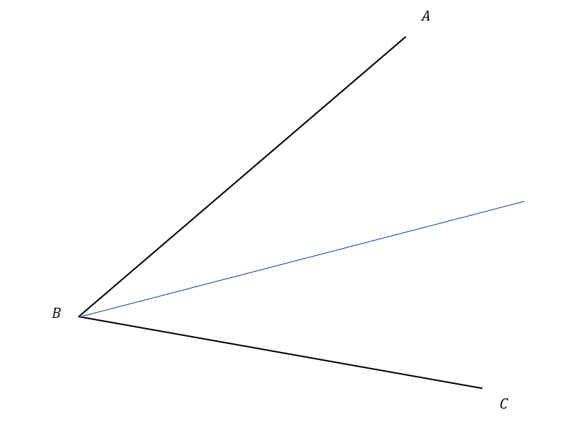
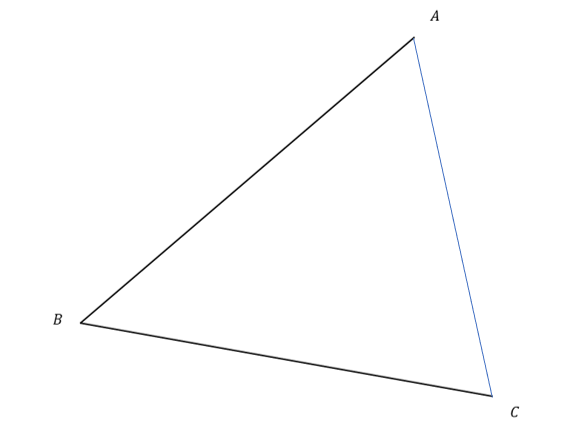
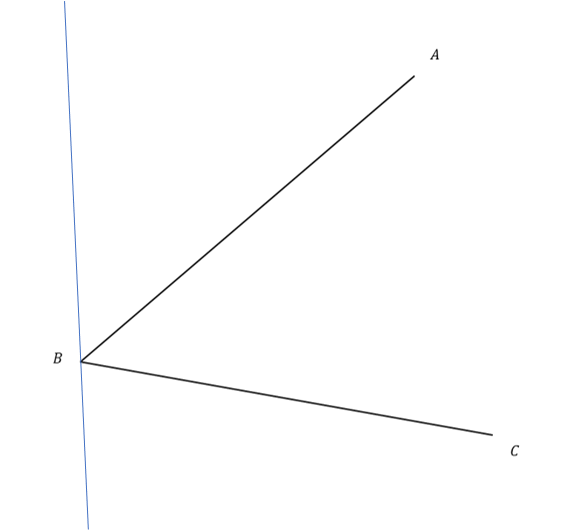
Which diagram shows a bisection of the angle ABC.
ANSWER: Multiple Choice (Type 2)
A:
B:

C:
D:
Answer: A
Workings:
The diagram shown features a line that splits the angle ABC into two equal parts and therefore bisects it.
Marks = 2
Question 5
Triangle ABC is shown below
AC=7 cm
CB=5 cm
AB=8 cm
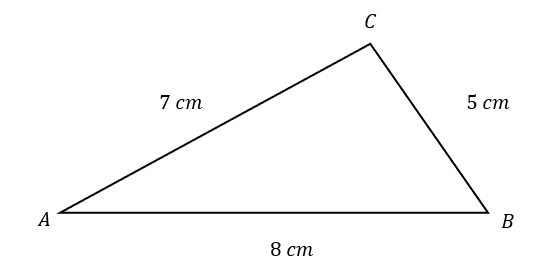
Given that line AB has already been drawn, which diagram shows the construction lines required to accurately draw triangle ABC?
ANSWER: Multiple Choice (Type 2)
A:
B:
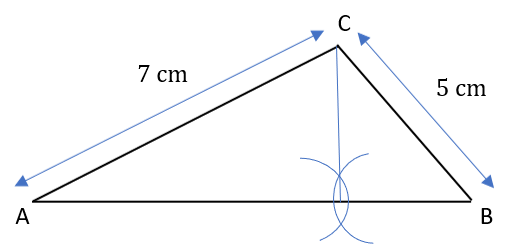
C:
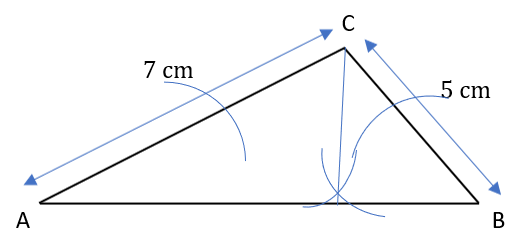
D:
Answer: A
Workings:
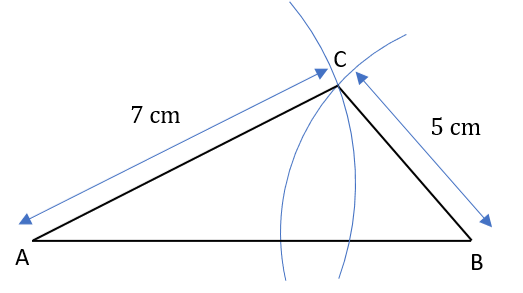
Place a compass on point A, extend it to 7 cm and draw an arc.
Place it on point B, extend it to 5 cm and draw an arc.
Draw a line from the point of intersection of the arcs to both points A and B.
This gives the required triangle.
Marks = 3
Question 6
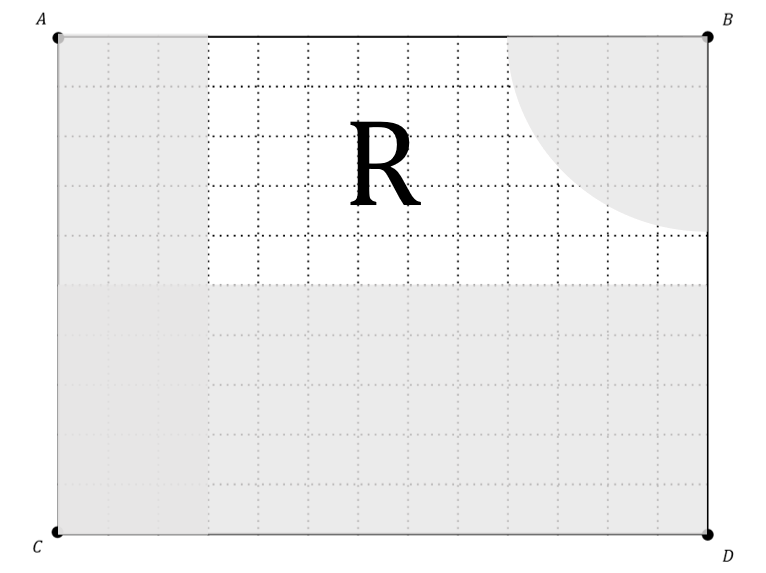
A scale plan for a garden is shown below.
Some of the key features are missing from the diagram.
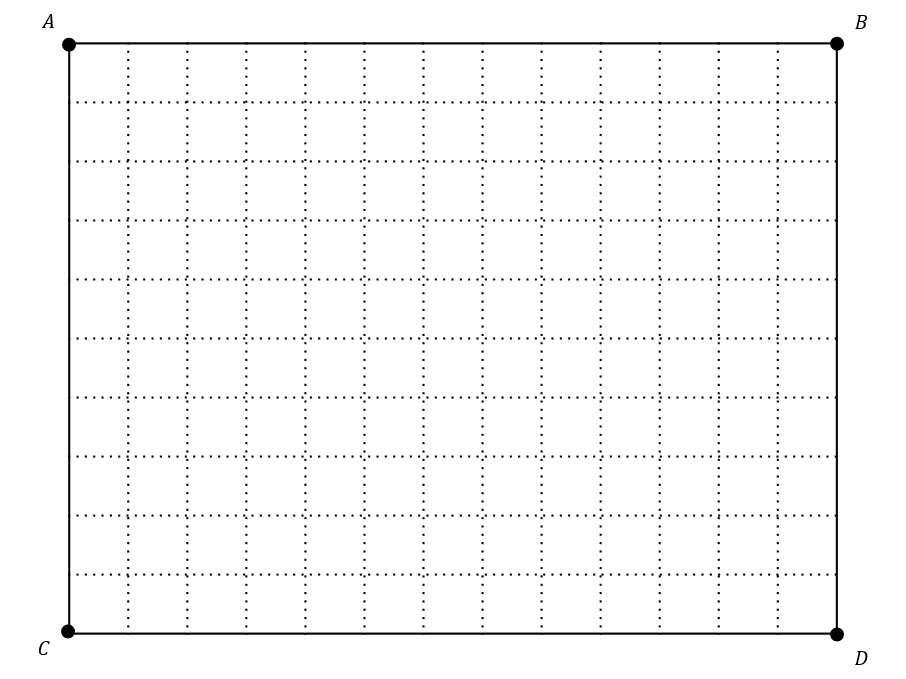
Decking covers a region that is 3 m from AC
Decking also covers a region that is 4 m from C.
Decking will also cover all the regions closer to DB than CD.
The area not covered by decking is marked with an R.
The scale for the plane is 1 square = \, 1 m
ANSWER: Multiple Choice (Type 2)
A:

B:
C:

D:

Answer: A
Workings:
There will be an area of decking of width 3 and length 10 on the far left hand side of the diagram.
The area of decking 4 metres from point C will consist of a circle quarter, as C is in a corner.
This circle sector will have radius 4, with C acting as the circle centre.
The final section of decking covers all points closer to DB than CD.
Because these two lines intersect at point D, the edge of the decking can be shown as a line connecting points A and D.
The decking will be placed above the line.
Marks = 3
Question 7
Triangle ABC is shown below
CAB=45\degree
CBA=45\degree
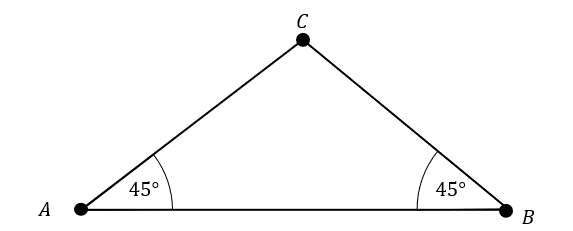
Which diagram shows the construction lines for an accurate drawing of ABC , with AB as a starting line?
![]()
ANSWER: Multiple Choice (Type 2)
A:
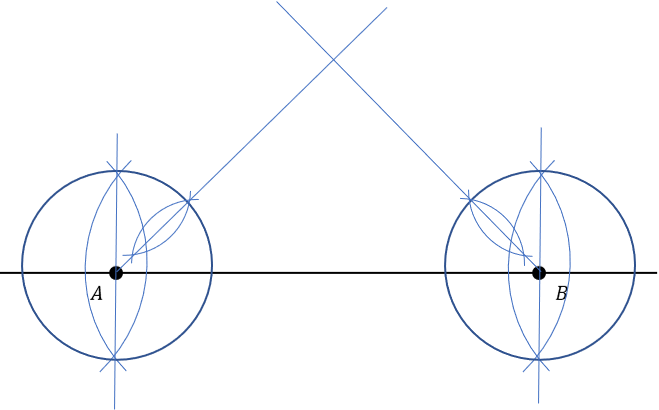
B:
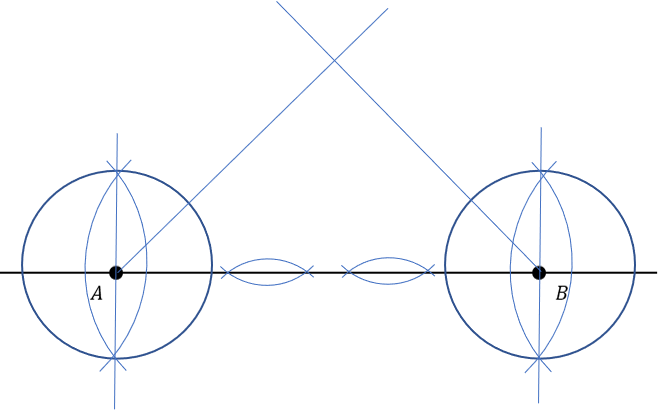
C:
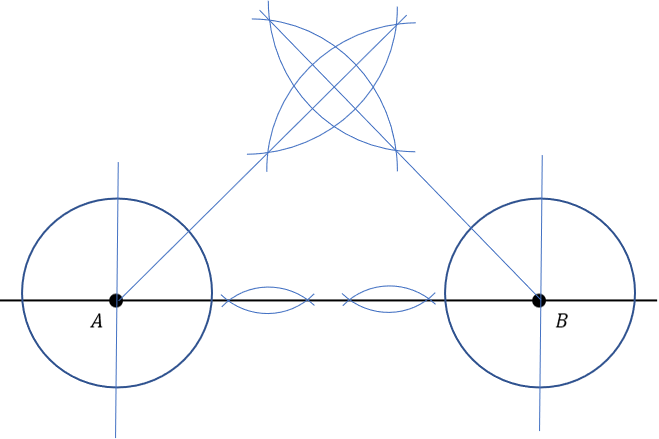
D:
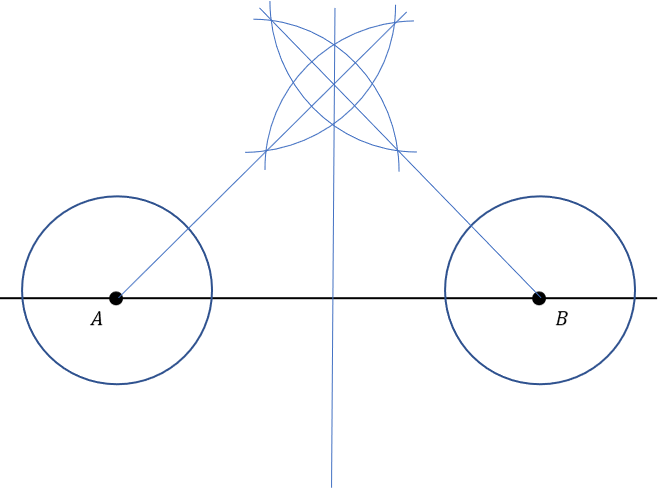
Answer: A
Workings:
Start by drawing a circle around point A.
Place the compass on a point of intersection between the circle and the extended line AB. Draw an arc of radius greater than the distance between the centre of the circle and point of intersection.
Do the same for the other point of intersection.
Draw a line that passes through the two points of intersection of the arcs just drawn. This is perpendicular to line AB.
From the point of intersection of the perpendicular line and the circle, draw an arc, then draw another from the point of intersection of the circle and lineAB.
Draw a line passing through the intersection points of these two new arcs, called AC.
Complete all previous steps for point B, creating the line BC at the end.
Therefore the lines AB, AC and BC form the isosceles triangle ABC shown in the question.
Marks = 3
