Question 1
The diagram below shows a regular pentagon.
ABC is a straight line
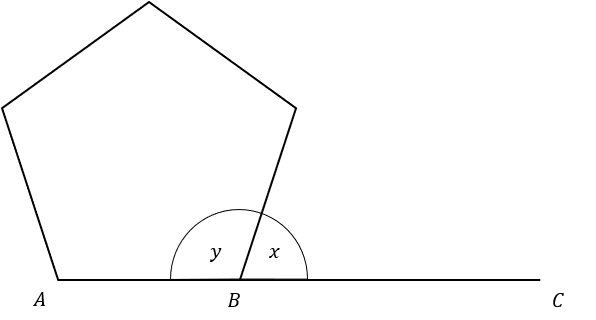
1(a):
Find x
ANSWER: Multiple Choice (Type 1)
A: 80\degree
B: 66\degree
C: 72\degree
D: 75\degree
Answer: C
Workings:
The formula for the exterior angle of a shape with n sides is \dfrac{360}{n}
The shape has 5 sides so the Exterior Angle, x=\dfrac{360}{5}=72\degree
Marks = 2
1(b):
Find y
ANSWER: Multiple Choice (Type 1)
A: 100\degree
B: 105\degree
C: 114\degree
D: 108\degree
Answer: D
Workings:
Angles on a straight line add up to 180 so we can subtract x from 180 to find y
180-72=108\degree
Marks = 2
Question 2
The diagram below shows a regular polygon.
The exterior angle is 20°

Find the number of sides of the polygon shown above.
ANSWER: Simple Text Answer
Answer: 18
Workings:
Rearranging the formula for the exterior angle we get number of sides, n=\dfrac{360}{Exterior Angle}
So in this case n=\dfrac{360}{20}=18
Marks = 2
Question 3
The diagram below shows a regular hexagon.
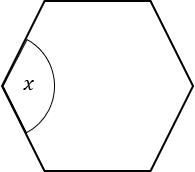
Find the value of x
ANSWER: Multiple Choice (Type 1)
A: 110\degree
B: 120\degree
C: 130\degree
D:140\degree
Answer: B
Workings:
The sum of interior angles in a polygon is (n-2)\times 180
In this case, the sum of interior angles = (6-2)\times 180 = 720
Dividing this by the number of sides gives x=\dfrac{720}{6}=120
Marks = 2
Question 4
The diagram shows a regular hexagon and regular pentagon attached

Find the value of x
ANSWER: Multiple Choice (Type 1)
A: 119\degree
B:125\degree
C: 132\degree
D: 139\degree
Answer: C
Workings:
We can find x by summing the exterior angles for the Hexagon and Pentagon
\dfrac{360}{5}+\dfrac{360}{6}=72+60=132
Marks = 2
Question 5
The diagram below shows an irregular heptagon

Find the value of x
ANSWER: Multiple Choice (Type 1)
A: 145\degree
B: 152\degree
C: 160\degree
D: 167\degree
Answer: A
Workings:
Using the equation for sum of interior angles
(7-2)\times 180 = 900
Find the sum of the existing angles
110+120+140+135+120+130=755
To find x subtract the sum of existing angles from the total sum of angles.
900-755=145\degree
Marks = 3
Question 6
The diagram below shows an irregular hexagon.
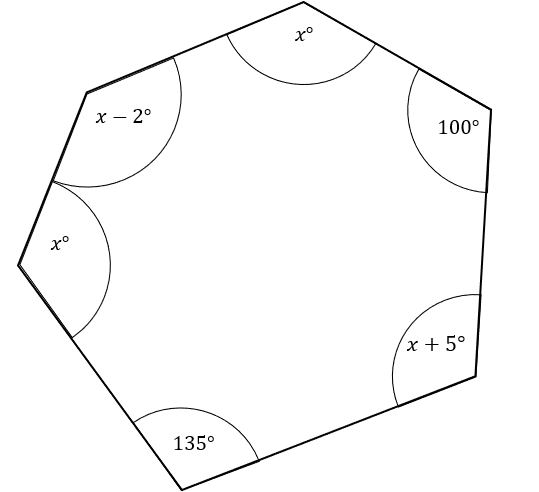
Find the value of x to 1 dp
ANSWER: Simple Text Answer
Answer: 120.5
Workings:
Using the equation for sum of interior angles
(6-2)\times 180 = 720
This is equal to the sum of the given angles, so
x+100+x+5+135+x+x-2=4x+238=720
Rearranging gives 482=4x
x=120.5\degree
Marks = 3
