Question 1
Below shows different parts of a circle indicated by an arrow.
X indicates the centre of the circle.
Match each part of a circle with the correct name.
One has been done for you.

1(a):
Which diagram shows the Arc?
ANSWER: Multiple Choice (Type 1)
A: Circle A
B: Circle B
C: Circle C
D: Circle D
E: Circle E
Answer: D
Workings:
An Arc is a section of the circle’s circumference.
Marks = 1
1(b):
Which diagram shows the Chord?
ANSWER: Multiple Choice (Type 1)
A: Circle A
B: Circle B
C: Circle C
D: Circle D
E: Circle E
Answer: B
Workings:
A Chord is a line that connects two different points on a circle’s circumference.
Marks = 1
1(c):
Which diagram shows the Sector?
ANSWER: Multiple Choice (Type 1)
A: Circle A
B: Circle B
C: Circle C
D: Circle D
E: Circle E
Answer: C
Workings:
A Sector is an area bounded by two different radii and an arc of the circle.
Marks = 1
1(d):
Which diagram shows the Diameter?
ANSWER: Multiple Choice (Type 1)
A: Circle A
B: Circle B
C: Circle C
D: Circle D
E: Circle E
Answer: E
Workings:
The Diameter is a line that connects two points on the circumference while also passing through the centre.
Marks = 1
1(e):
Which diagram shows the Tangent?
ANSWER: Multiple Choice (Type 1)
A: Circle A
B: Circle B
C: Circle C
D: Circle D
E: Circle E
Answer: A
Workings:
A Tangent is a line that touches a single point on the circumference of the circle but does not cross it.
Marks = 1
Question 2
Consider the following circle with centre at X and radius of 3.7 m.

2(a):
Find the diameter of this circle in metres.
ANSWER: Simple Text Answer
Answer: 7.4
Workings:
The diameter of a circle is twice the radius.
2\times 3.7 = 7.4
Marks = 1
2(b):
Find the circumference of this circle to 2 decimal places in metres.
ANSWER: Simple Text Answer
Answer: 23.25
Workings:
Circumference = \pi\times diameter
= \pi \times 7.4 = 23.25 m
Marks = 2
Question 3
The circle below has centre O and radius 3.6 cm

3(a):
Find the circumference of the circle, giving your answer in terms of \pi.
ANSWER: Multiple Choice (Type 1)
A: 7.0\pi cm
B: 7.2\pi cm
C: 7.4\pi cm
D: 7.6\pi cm
Answer: B
Workings:
The diameter is twice the radius, so diameter = 7.2 cm
\text{Circumference} = \pi \times \text{Diameter} = 7.2 \pi cm
Marks = 2
3(b):
Find the area of the circle.
Give your answer to 1 decimal place in cm^2.
ANSWER: Simple Text Answer
Answer: 40.7 cm^2
Workings:
Area = \pi \times radius^2 = \pi \times 3.6^2 = 40.7 cm^2
Marks = 2
Question 4
The semi-circle below has centre O and a radius of 8 cm.
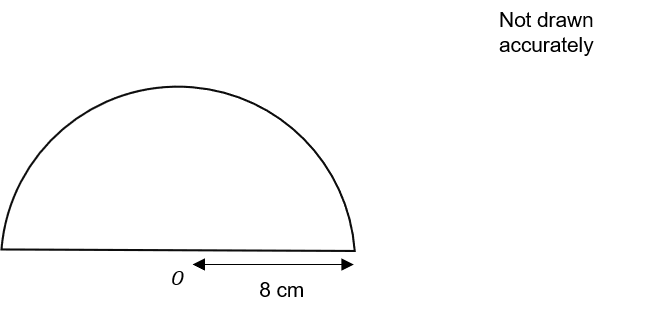
Find the perimeter of the semi-circle.
Give your answer to 1 decimal place in cm.
ANSWER: Simple Text Answer
Answer: 41.1
Workings:
We can find the length of the arc of the semi-circle using
\dfrac{1}{2}\times \pi \times 16 = 25.13
Add this to the diameter to get
25.13+16 = 41.1 cm (1 dp)
Marks = 3
Question 5
The circle below has centre O and a radius of x cm
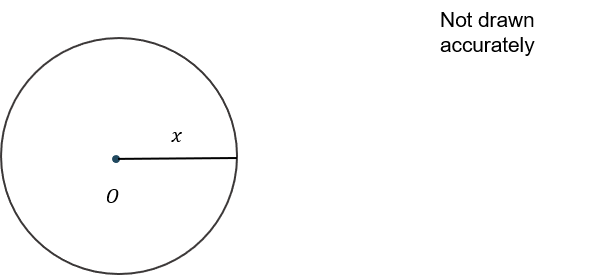
The area of the circle is 150 cm^2
Find the value of x.
Give your answer to 1 decimal place in cm.
ANSWER: Simple Text Answer
Answer: 6.9
Workings:
\pi \times x^2 = 150
x^2=\dfrac{150}{\pi}
x = 6.9 cm
Marks = 3
Question 6
Circle A has a radius of 16 cm
Circle B has a radius of 7 cm

6(a):
Calculate the area of circle A in terms of \pi.
ANSWER: Multiple Choice (Type 1)
A: 248\pi cm^2
B: 252\pi cm^2
C: 256\pi cm^2
D: 260\pi cm^2
Answer: C
Workings:
Area = \pi \times radius^2 = \pi \times 16^2 = 256\pi cm^2
Marks = 1
6(b):
Calculate the shaded area in cm^2.
Give your answer to 1 decimal place.
ANSWER: Simple Text Answer
Answer: 650.3
Workings:
First calculate the area of the Circle B
\pi \times 7^2 = 49\pi
Subtract this from the area of Circle A to get the shaded area
256\pi - 49\pi = 207\pi = 650.3 cm^2 (1 dp)
Marks = 2
Question 7
The largest circle in the diagram below has a radius of 10 m.
The radius of the white circle is 7 m.
Each small grey circle has a diameter of 2 m.
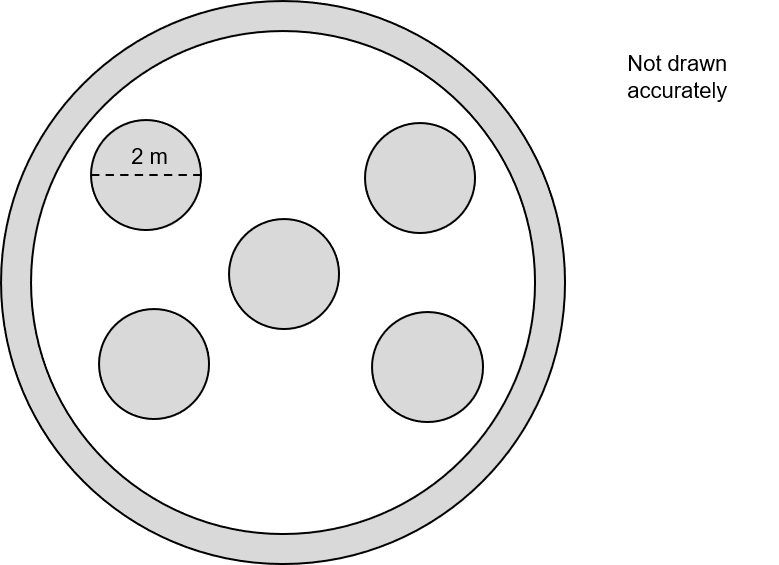
What percentage of the area in the diagram is shaded?
ANSWER: Multiple Choice (Type 1)
A: 44\%
B: 48\%
C: 52\%
D: 56\%
Answer: D
Workings:
First find the area of the largest circle
\pi \times 10^2 = 100\pi
Find the area of the white circle
\pi \times 7^2 = 49\pi
Subtract the area of the white circle from the largest circle to get the area of the outer shaded area
100\pi - 49\pi = 51\pi
The area of the five small shaded circles is
5\times \pi \times 1^2 = 5\pi
Add this to the area of the outer shaded area to get
51\pi + 5\pi = 56\pi
Divide this by the area of the largest circle to get
\dfrac{56\pi}{100\pi} = 0.56
So 56\% of the diagram is shaded.
Marks = 4
Question 8
A set of circles have radii in the ratio 1 : 2 : 3 : 5
What is the ratio of their areas?
Give your answer in its simplest terms.
ANSWER: Multiple Choice (Type 1)
A: 1 : 4 : 9 : 25
B: 2 : 3 : 4 : 5
C: 1 : 3 : 5 : 7
D: 1 : 5 : 10 : 25
Answer: A
Workings:
Each radius is multiplied by itself so we would square the radius ratios to get the correct area ratios
1^2 : 2^2 : 3^2 : 5^2
= 1 : 4 : 9 : 25
Marks = 2
Question 9
The diagram below shows a square inside a circle.
The vertices of the square touch the circumference of the circle.
The radius of the circle below is 6 cm.

9(a):
Calculate the area of the square, ABCD in cm^2
ANSWER: Simple Text Answer
Answer: 72
Workings:
The radius of the circle is the same as a line from the centre of the square to one of its corners
This means we have an isosceles right angled triangle connecting two adjacent corners to the centre.
We can calculate the side length of the square with
\sqrt{6^2 + 6^2} = 6\sqrt{2}
The area is therefore
(6\sqrt{2})^2 = 72 cm^2
Marks = 3
9(b):
Calculate the shaded area between the circle and the square.
Give your answer to 1 dp in cm^2
ANSWER: Simple Text Answer
Answer: 41.1
Workings:
Calculate the area of the circle
\pi \times 6^2 = 36\pi
We can find the shaded area by subtracting the area of the square from the area of the circle
36\pi - 72 = 41.1 cm^2
Marks = 2
