Question 1
Points A, B, and C are all on the circumference of the circle.
O represents the centre.

Calculate the angle x, giving a reason for your answer.
ANSWER: Multiple Choice (Type 1)
A: 47\degree
B: 48\degree
C: 49\degree
D: 50\degree
Answer: C
Workings:
The angle at the centre of a circle is twice the angle at the circumference
Marks = 2
Question 2
Points A, B, and C lie on the circumference of a circle.
The line BC passes through the centre of the circle, O.

Calculate the angle x.
ANSWER: Multiple Choice (Type 1)
A: 58\degree
B: 56\degree
C: 54\degree
D: 52\degree
Answer: A
Workings:
The angle opposite the diameter is a right angle.
x = 180 - 90 - 32 = 58\degree
Marks = 2
Question 3
The diagram below shows a cyclic quadrilateral ABCD.
Points A,B,C and D touch the circumference of the circle.
Line BD goes through centre O.

Work out the size of the angle marked x.
ANSWER: Multiple Choice (Type 1)
A: 80\degree
B: 90\degree
C: 100\degree
D: 110\degree
Answer: B
Workings:
The angle opposite the diameter is a right angle.
So x = 90\degree
Marks = 2
Question 4
Points A, B, and C are all on the circumference of a circle.
O represents the centre.

Calculate the angle x.
ANSWER: Multiple Choice (Type 1)
A: 30\degree
B: 35\degree
C: 40\degree
D: 45\degree
Answer: D
Workings:
Triangle AOC is Isosceles, so angle ACO = 22\degree
Triangle BOC is also Isosceles so angle BCO = 67\degree
Find angle BCA by subtracting angle ACO from angle BCO
67 - 22 = 45\degree
Marks = 2
Question 5
Points A, B, and C are all on the circumference of the circle.
O represents the centre.
DA and DC are tangents to the circle.
Angle CDO = 22 \degree

Calculate the angle x.
ANSWER: Multiple Choice Answer
A: 62\degree
B: 64\degree
C: 66\degree
D: 68\degree
Answer: D
Workings:
Two tangents drawn from an outside point are equal in length and create right angled triangles
So OAC and OCD are both 90\degree
To find angle COD
180-90-22 =68
Because the two right angled triangles are congruent
Angle AOD = COD = 68\degree
Therefore angle COA = 136\degree
Because the angle at the centre of a circle is twice the angle at the circumference
Angle ABC = \dfrac{1}{2}AOC = 68\degree = x
Marks = 4
Question 6
Points A, B, C, and D are all on the circumference of the circle.
Point X is the intersection between line AC and line DB
Angle CXB = 110 \degree
Angle XAB = 22 \degree
Angle BCX = 23 \degreee
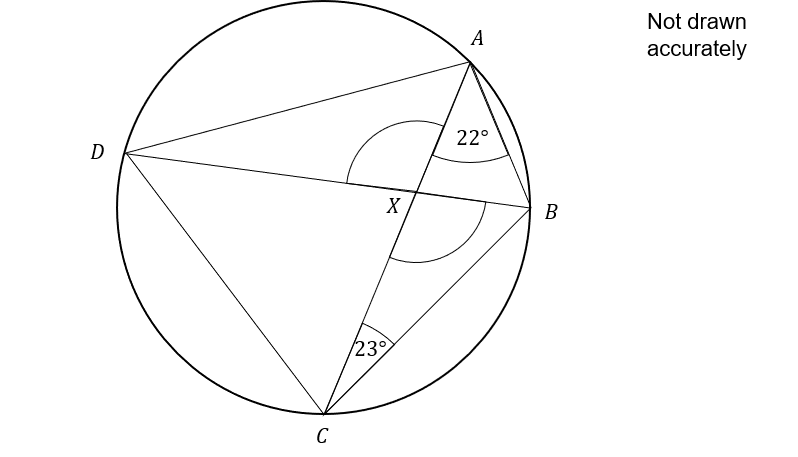
6(a):
Calculate the angle XBC
ANSWER: Multiple Choice (Type 1)
A: 47\degree
B: 50\degree
C: 53\degree
D: 56\degree
Answer: A
Workings:
Angles in a triangle add up to 180
XBC = 180 - 110 - 23 = 47\degree
Marks = 1
6(b):
Calculate the angle DAX
ANSWER: Multiple Choice (Type 1)
A: 41\degree
B: 43\degree
C: 47\degree
D: 50\degree
Answer: C
Workings:
Angles DAC and DBC are in the same segment of the chord DC so DAC = DBC = 47\degree
Marks = 2
Question 7
Points A, B, and C are all on the circumference of the circle.
O represents the centre.
Angle DOB = 2x+28
Angle DCB = 3x-70

Calculate the value of x.
ANSWER: Multiple Choice (Type 1)
A: 50\degree
B: 54\degree
C: 56\degree
D: 59\degree
Answer: D
Workings:
The angle at the centre of a circle is twice the angle at the circumference.
Because of this we know DAB = \dfrac{1}{2}DOB = \dfrac{1}{2}(2x+28) = x+14
Because points A, B, C and D all lie on the circumference of the circle so ABCD is a cyclic quadrilateral.
Opposite angles in a cyclic quadrilateral add up to 180\degree
3x-70+x+14 = 180
This can be rearranged to get
4x-56 = 180
x = 59\degree
Marks = 3
Question 8
Points A, B and C are on the circumference of a circle, with centre O.
Points C, D and E lie on a tangent line.
AB = AC
Calculate angle CDO.
ANSWER: Multiple Choice (Type 1)
A: 39\degree
B: 46\degree
C: 41\degree
D: 48\degree
Answer: A
Workings:
Triangle OBC is an isosceles triangle, so the base angles are identical.
We can calculate angle COB as 180-46-46=88
The angle at the centre of a circle is twice the angle at the circumference
BAC = \dfrac{1}{2}BOC = \dfrac{1}{2}\times 88 = 44\degree
ABC is an isosceles triangle so angles ABC = ACB = \dfrac{180-44}{2} = 68
Angle ACO = 68-46 = 22\degree
Angle DCO = 90\degree as a radius meets a tangent
Angle DCF = 90 - ACO = 90 - 22 = 68\degree
Angles on a straight line add up to 180\degree
Angle DFC = 180-107 = 73\degree
CDF = CDO = 180 - 68 - 73 = 39\degree
Marks = 5
