Question 1: [5 marks]
Line ABC is parallel to line DE.
\angle DAE = 13 \degree
\angle EAC = 31 \degree
DE = BC = 3 cm

Find the length of EC.
Give your answer to the nearest cm.
Answer type: Simple text answer
ANSWER: 5 cm
WORKING:

\dfrac{AE}{\sin(136)} = \dfrac{3}{\sin(13)}
AE = 9.2641...

\sin(31) = \dfrac{EC}{9.2641...}
EC = 4.7714... = 5 cm (nearest cm)
Question 2: [5 marks]
Two triangles CDB and ADB are joined along DB, shown below.
DC = 6 cm
CB = 7 cm
DB = 5 cm
BA = x cm
\angle DAB = 30 \degree
Find x from the diagram above.
Give your answer to 1 decimal place.
Answer type: Simple text answer
ANSWER: 9.8 cm
WORKING:
\cos(CDB) = \dfrac{6^2 + 5^2 - 7^2}{2(6)(5)} = 0.2
CDB = 78.4630 \degree
ADB = 180 - 78.4630 = 101.5470 \degree
\dfrac{x}{\sin(101.5470)} = \dfrac{5}{\sin(30)}
x = 9.8 cm (1 dp)
Question 3: [4 marks]
The tallest point of a building is given the letter A, shown below.
Points B and C are horizontal to the ground such that angle ABC is 22 \degree and ACB is 18 \degree, shown below.
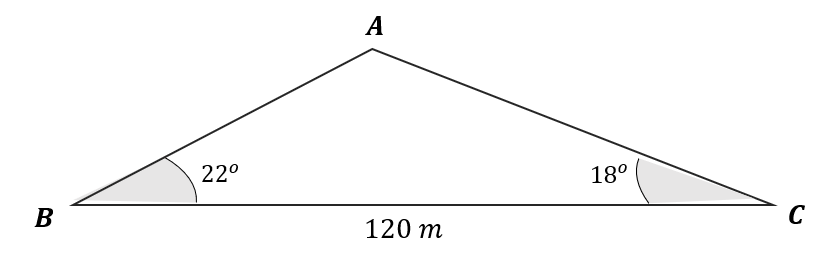
Given that the distance BC = 120 m, calculate the height of the building to the nearest metre.
Answer type: Simple text answer
ANSWER: 22 m
WORKING:

\dfrac{120}{\sin(140)} \times \sin(18) = 57.6894... m
h = 57.6894... \times \sin(22) = 21.61 = 22 m (nearest metre)
Question 4: [5 marks]
Allan is building an enclosure in his garden.
It is in the shape of the quadrilateral below.
AB = 5.3 m
BC = 6.4 m
BD = 6.2 m

Calculate the perimeter of the enclosure.
Give your answer to the nearest metre.
Answer type: Simple text answer
ANSWER: 25 m
WORKING:
\dfrac{\sin(ADB)}{5.3} = \dfrac{\sin(70)}{6.2}
ADB = 53.445...
DBA = 190 - 53.445... = 56.555...
\dfrac{AD}{\sin(56.555...)} = \dfrac{6.2}{\sin(70)}
AD = 5.5053...
\dfrac{\sin(BDC)}{6.4} = \dfrac{\sin(50)}{6.2}
BDC = 52.256...
DBC = 77.7438...
\dfrac{DC}{\sin(77.7438...)} = \dfrac{6.2}{\sin(50)}
DC = 7.9190...
\text{Perimeter } = 5.3 + 6.4 + 5.5053... + 7.9190... = 25 m (nearest metre)
Question 5: [5 marks]
The quadrilateral ABCD, is made up of two triangle ABD and BCD.
AB = 5.1 m
AD = 6.2 m
CD = 7.9 m

Find the angle ADB, shown on the diagram above.
Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 48.98 \degree
WORKING:
\dfrac{BD}{\sin(47)} = \dfrac{7.9}{\sin(71)}
BD = \dfrac{7.9}{\sin(71)} \times \sin(47) = 6.11 (2 dp)
\cos(x) = \dfrac{6.1^2 + 6.2^2 - 5.1^2}{2(6.1)(6.2)} = 0.656...
x = 48.98 \degree (2 dp)
Question 6:
Sophia and Grace are travelling in their cars away from a crossroads at O shown below.
Sophia is traveling to D through point A.
Grace is traveling to E, through point B.
AB=182.3 m
OA=170 m
AD=200 m
BE=300 m

Question 6(a): [4 marks]
Find the distance DE.
Give your answer to the nearest metre.
Answer type: Simple text answer
ANSWER: 452 m
WORKING:
\cos(EOD) = \dfrac{170^2 + 180^2 - 182.3^2}{2(170)(180)} = 0.4586...
EOD = 62.7023... \degree
DE^2 = 370^2 + 480^2 - 2(370)(480) \cos(62.7023...)
DE = 452.11... = 452 m (nearest metre)
Question 6(b): [3 marks]
Find the bearing of E from D.
Give your answer to the nearest degree.
Answer type: Simple text answer
ANSWER: 70 \degree
WORKING:
\dfrac{\sin(ODE)}{480} = \dfrac{\sin(62.7023...)}{452.11...}
ODE = 71 \degree (nearest degree)
