Question 1
A cuboid is pictured in the diagram below.
EH=4cm
GH = 3cm
CG=12cm

1(a):
Find the length CH to 2 decimal places.
ANSWER: Simple Text Answer
Answer: 12.37 cm
Workings:
CH^2 = 12^2 + 3^2 = 144 + 9 = 153
CH = \sqrt{153}
CH = 12.37 cm (2 dp)
Marks = 2
1(b):
Using your previous answer, find the length CE.
Give your answer to 2 decimal places.
ANSWER: Simple Text Answer
Answer: 13.00 cm
Workings:
CE^2 = 12.37^2 + 4^2 = 153.01 + 16 = 169.01
CE = \sqrt{169.01}
CE = 13.00 cm (2dp)
Marks = 2
Question 2
A cuboid is pictured in the diagram below.
AB=7 m
BC=5m
CY=5m
X is the midpoint of AE
Y is the midpoint of CG

2(a):
Find the length XY.
Give your answer to 2 decimal places
ANSWER: Simple Text Answer
Answer: 8.60 m
Workings:
CA^2 = 5^2 + 7^2 = 25 + 49 = 74
CA = \sqrt{74}
CA = 8.60
XY=CA=8.60 m
Marks = 2
2(b):
Using your answer to part (a), find the length CX.
Give your answer to 2 decimal places.
ANSWER: Simple Text Answer
Answer: 9.95 cm
Workings:
CX^2 = 5^2 + 8.6^2 = 25 + 73.96 = 98.96
CX = \sqrt{98.96}
CX = 9.95 cm (2 dp)
Marks = 2
Question 3
A square-based pyramid has the following properties.
Length DC=12 cm
The vertical height = 10 cm
Point X is the centre of the square base.
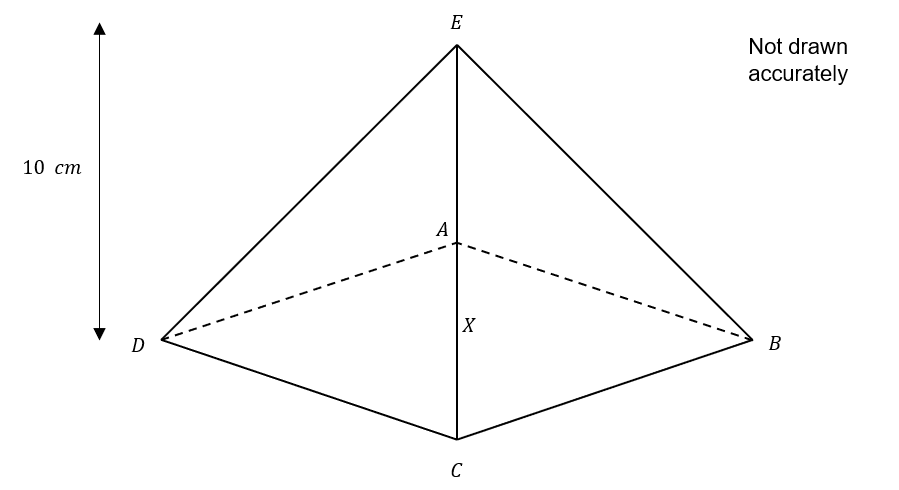
3(a):
Find length AE
Give your answer to 2 decimal places.
ANSWER: Simple Text Answer
Answer: 13.11 cm
Workings:
AC^2 = 12^2 + 12^2 = 144 + 144 = 288
AC = \sqrt{288}
AE^2 = 10^2 + (\dfrac{\sqrt{288}}{2})^2=100 + 72.08 = 172.08
AE = \sqrt{172.08} = 13.11 cm
Marks = 2
3(b):
Find the angle AEB
Give your answer to 2 decimal places.
ANSWER: Simple Text Answer
Answer: 54.45°
Workings:
cos(A)=\dfrac{(13.11^2+13.11^2)-12^2}{2\times 13.11\times 13.11} = 0.581
A = cos^{-1}(0.581) = 54.45\degree
Marks = 2
Question 4
The diagram below shows an isosceles triangular prism.
AC=8cm
Angle BCA=50°
Angle FCE=40°

Find the length EC.
Give your answer to 2 decimal places.
ANSWER: Simple Text Answer
Answer: 9.68 cm
Workings:
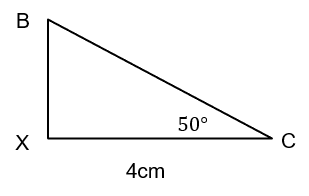
cos(50) = \dfrac{4}{BC}
BC = \dfrac{4}{cos(50)} = 6.22 cm
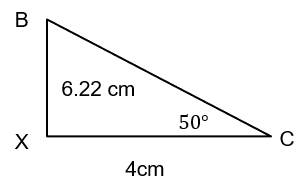
sin(40) = \dfrac{6.22}{EC}
EC = \dfrac{6.22}{sin(40)} = 9.68 cm
Marks = 3
Question 5
The diagram shows a tetrahedron
All faces are equilateral triangles with side length 2m.
Point X lies directly below point D.

Find the length DX
Give your answer to 2 decimal places.
ANSWER: Simple Text Answer
Answer: 1.63 m
Workings:
cos(30) = \dfrac{1}{AX}
AX = \dfrac{1}{cos(30)}=\dfrac{2\sqrt{3}}{3}m
XD^2 = 2^2 - (\dfrac{2\sqrt{3}}{3})^2 = 4 - \dfrac{4}{3} = \dfrac{8}{3}
XD = \sqrt{\dfrac{8}{3}} = 1.63 m (2dp)
Marks = 3
Question 6
In the triangular prism below
AC=7cm
Angle BCA=75°
Angle FCE=35°

Calculate the volume of the prism.
Give your answer to 1 decimal place.
ANSWER: Simple Text Answer
Answer: 882.9 cm^3
Workings:
cos(75) = \dfrac{3.5}{BC}
BC = \dfrac{3.5}{cos(75)} = 13.52 cm
CF = \dfrac{13.53}{tan(35)} = 19.31 cm
Area = \dfrac{1}{2}\times 13.52\times 7\times sin(75) = 45.71 cm^2
45.71\times 19.31 = 882.9 cm^3
Marks = 4
Question 7
The diagram below shows a doorstop, modelled as a triangular prism.
Angle ABC=90°
Angle ACB=30°
BC=4cm
AD=2ABX is a point on the centre of the face ADFC.
AX = \dfrac{a\sqrt{6}}{3}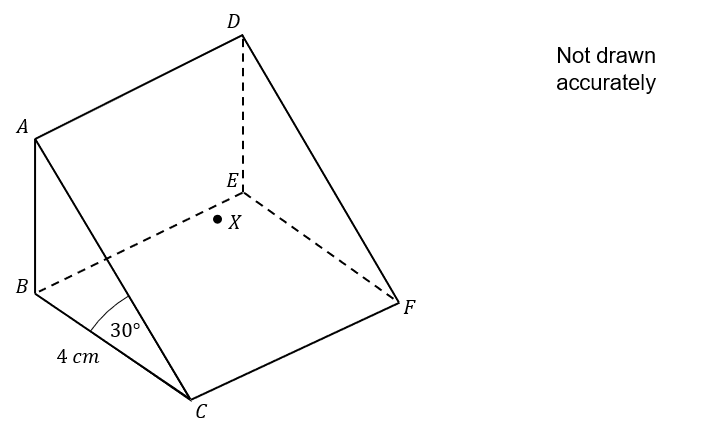
Find the value of a.
ANSWER: Simple Text Answer
Answer: 4
Workings:
tan(30) = \dfrac{AB}{4}
AB = 4\times tan(30) = \dfrac{4\sqrt{3}}{3}
AD = 2AB = 2\times \dfrac{4\sqrt{3}}{3}=\dfrac{8\sqrt{3}}{3}
cos(30) = \dfrac{4}{AC}
AC = \dfrac{4}{cos(30)} = \dfrac{8\sqrt{3}}{3}
DC^2 = (\dfrac{8\sqrt{3}}{3})^2 + (\dfrac{8\sqrt{3}}{3})^2 = \dfrac{128}{3}
DC = \dfrac{8\sqrt{6}}{3}
DX = DC\div 2 = \dfrac{4\sqrt{6}}{3}
AX = BX = DX = CX
a = 4
Marks = 5
