Question 1:
The likelihood of an event taking place is marked by a cross on the following probability scales. Match up the following events with the probability scales shown.
1(a) Getting ‘heads’ on a coin flip
ANSWER: Multiple Choice (Type 1)
A: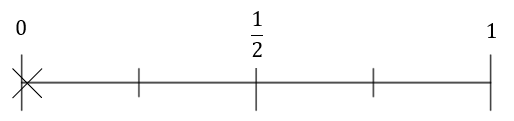
B: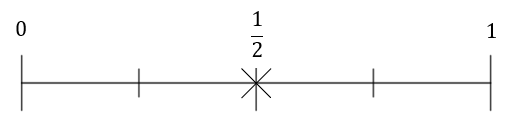
C: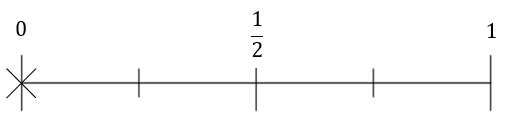
D: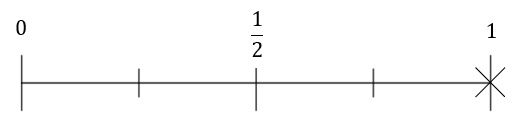
Answer: B
Marks = 1
1(b) Winning the lottery
ANSWER: Multiple Choice (Type 1)
A:
B:
C:
D:
Answer: A
1(c) The sun comes up tomorrow
ANSWER: Multiple Choice (Type 1)
A:
B:
C:
D:
Answer: D
1(d) Roll a 0 on a fair standard dice
ANSWER: Multiple Choice (Type 1)
A:
B:
C:
D:
Answer: C
Question 2:
A bag contains 12 coloured counters.
3 of the counters are blue
6 of the counters are red
3 of the counters are green.
Tom takes a counter at random from the bag.
On the probability scale, mark with a cross the probability that Tom takes the following:
2(a) a blue counter
A: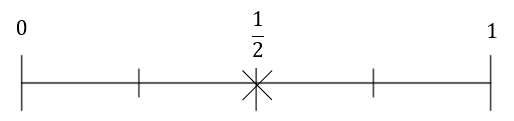
B: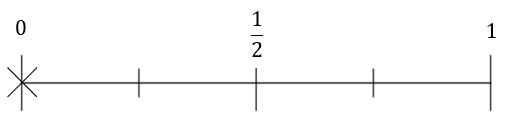
C: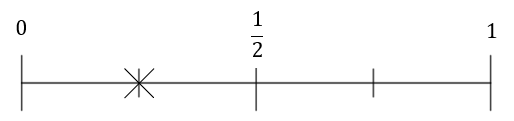
Answer: C
Workings:
There are 12 counters in total, 3 of which are blue. The probability of drawing a blue counter is therefore \dfrac{3}{12}=\dfrac{1}{3}
Marks = 1
2(b) a red counter
A:
B:
C:
Answer: A
Marks = 1
2(c) an orange counter
A:
B:
C:
Answer: B
Marks = 1
Question 3:
Peter rolls an ordinary 6 sided dice.
Question 3(a): [1 mark]
What is the probability that he rolls a 6?
Answer type: Multiple choice type 1
A: \dfrac{1}{2}
B: \dfrac{1}{3}
C: \dfrac{1}{6}
D: 1
ANSWER: C: \dfrac{1}{6}
Question 3(b): [1 mark]
What is the probability that he rolls an even number?
Answer type: Multiple choice type 1
A: \dfrac{1}{2}
B: \dfrac{1}{3}
C: \dfrac{1}{6}
D: 1
ANSWER: A: \dfrac{1}{2}
Question 4:
The probabilities of a spinner landing on each of its three colours are shown in the table below.
Question 4(a): [1 mark]
Select the correct missing value from the table below.

Answer type: Multiple choice type 1
A: \dfrac{1}{2}
B: \dfrac{1}{3}
C: \dfrac{1}{6}
D: 1
ANSWER: A: \dfrac{1}{2}
WORKING:
Probabilities add up to 1, so the missing value is
1 - \dfrac{1}{3} - \dfrac{1}{6} = \dfrac{1}{2}
Question 4(b): [1 mark]
If the spinner is spun 180 times, how many times would you expect the spinner to land on blue?
Answer type: Simple text answer
ANSWER: 60
WORKING:
180 \times \dfrac{1}{3} = 60
Question 5: [1 mark]
Ben flips an unbiased coin 3 times.
He states he is more likely to get heads, tails, then heads than all tails for the three flips.
Is he correct?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: B: No
WORKING:
Ben is incorrect, the likelihood of both events is equal.
Question 6: [1 mark]
Three friends flip the same biased coin several times.
Their results are shown in the table below.
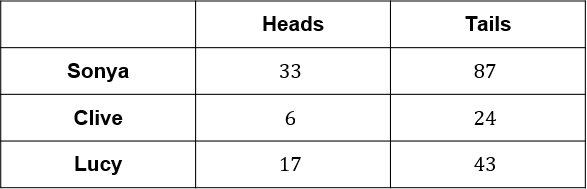
Each of the friends calculates their own probability of heads.
Which friend is likely to have the probability closest to the true probability?
Answer type: Multiple choice type 1
A: Sonya
B: Clive
C: Lucy
ANSWER: A: Sonya
WORKING:
Sonya is most likely to be the closest to the true probability because she did the most trials.
