Question 1
Anna records the speed of cars going past on a busy road.

Use this table to estimate the average speed of the cars.
Give your answer to 2 significant figures.
ANSWER: Simple Text Answer
Answer: 43 mph
Workings:
(15 \times 4) + (35\times 28) + (45\times 37) + (55\times 10) + (65\times 6) = 60 + 980 + 1665 + 550 + 390 = 3645
\dfrac{3645}{85} = 42.88mph
=43 mph to 2 significant figures.
Marks = 3
Question 2
Eric’s favourite bag of sweets says there are approximately 55 sweets in each bag.
Eric does an experiment to see if this is true.
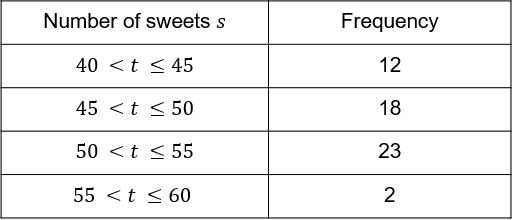
Use this table to estimate the average number of sweets in each bag.
Give your answer to 2 significant figures.
ANSWER: Simple Text Answer
Answer: 49
Workings:
(42.5\times 12) + (47.5\times 18) + (52.5\times 23) + (57.5\times 2) = 510 + 855 + 1207.5 + 115 = 2687.5
n = 12 + 18 + 23 + 2 = 55
\dfrac{2687.5}{55} = 49 sweets
Marks = 3
Question 3
A class of students all run 5km.
Their teacher records the time it takes them to finish.

Use this table to estimate the average time it took for students to finish the run.
Give your answer to 2 significant figures.
ANSWER: Simple Text Answer
Answer: 35 minutes
Workings:
(15\times 15) + (32.5\times 16) + (37.5\times 40) + (45\times 23) = 225 + 520 + 1500 + 1035 = 3280
n = 15 + 16 + 40 + 23 = 94
\dfrac{3280}{94} = 34.89
= 35 minutes to 2 significant figures.
Marks = 3
Question 4
Siobhan measures the temperature of different spots in the river.
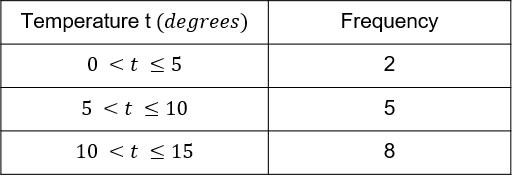
Use this table to estimate the average temperature of the river
Give your answer to the nearest degree.
ANSWER: Simple Text Answer
Answer: 10 degrees
Workings:
(2.5\times 2) + (7.5\times 5) + (12.5\times 8) = 5 + 37.5 + 100 = 142.5
n = 2 + 5 + 8 = 15
\dfrac{142.5}{15} = 9.5
= 10 degrees to nearest degree.
Marks = 3
Question 5
The following table displays the heights of children in Kevin’s class.
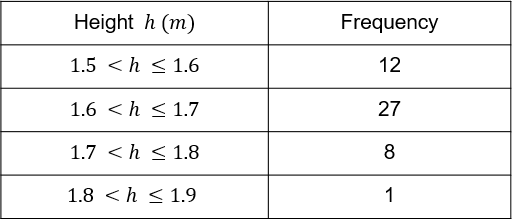
5(a)
Use this table to estimate the average height of the students in Kevin’s class.
Give your answer to one decimal place.
ANSWER: Simple Text Answer
Answer: 1.6 m
Workings:
(1.55\times 12) + (1.65\times 27) + (1.75\times 8) + (1.85\times 1) = 18.6 + 44.55 + 14 + 1.85 = 79
n = 12 + 27 + 8 + 1 = 48
\dfrac{79}{48} = 1.646
= 1.6 m to one decimal place.
Marks = 3
5(b):
Why is your answer to part (a) considered an estimate?
ANSWER: Multiple Choice (Type 1)
A: The distribution of data within each group is unknown.
B: A bigger group of data is needed.
C: It’s difficult to accurately measure someone’s height.
D: Doesn’t consider children shorter than 1.5 m and taller than 1.9 m
Answer: A
Workings:
It is impossible to tell, from the data given, where each child’s height lies in the group class.
The mean calculated in (a) just assumes that everyone in the group class has the same height, the midpoint.
Marks = 2
Question 6
Hannah wants to know the average diameter of cookies from her local bakery.
She measures 50 cookies.
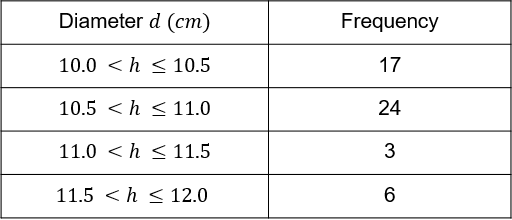
6(a):
What is the modal class?
ANSWER: Multiple Choice (Type 2)
A: 10.0 < h \leq 10.5
B: 10.5 < h \leq 11.0
C: 11.0 < h \leq 11.5
D: 11.5 < h \leq 12.0
Answer: B
Workings:
The modal class is the class with the highest frequency.
This is the class 10.5 < h \leq 11.0
Marks = 1
6(b):
Estimate the average diameter of the cookies.
ANSWER: Simple Text Answer
Answer: 10.7 cm
Workings:
(10.25\times 17) + (10.75\times 24) + (11.25\times 3) + (11.75\times 6) = 174.25 + 258 + 33.75 + 70.5 = 536.5
n = 17 + 24 + 3 + 6 = 50
\dfrac{536.5}{50} = 10.73
= 10.7 cm to 1 decimal place.
Marks = 3
