Question 1:
Ben flips an unbiased coin 2 times.
1(a) What are the values of x and y in the tree diagram below.
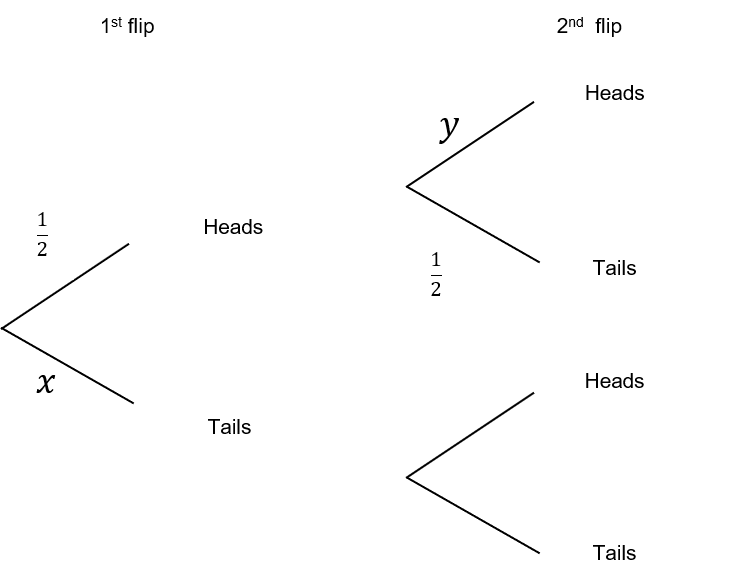
ANSWER: Multiple Choice (Type 1)
A: x= \dfrac{1}{2}, y=1
B: x=1, y=\dfrac{1}{2}
C: x=\dfrac{1}{2}, y=\dfrac{1}{2}
D: x=-\dfrac{1}{2},y= -\dfrac{1}{2}
Answer: C
Workings:
The probability of getting tails is always \dfrac{1}{2}. Each coin flip is an independent event.
Marks = 2
1(b) Hence, or otherwise, calculate the probability that both flips land on heads.
Give your answer as a fraction in its simplest form.
ANSWER: Fraction
Answer: \dfrac{1}{4}
Workings:
P(H,H)=\dfrac{1}{2}\times\dfrac{1}{2}=\dfrac{1}{4}
Marks = 2
Question 2
Dannielle has 7 balls in a bag. 3 of them are green and the rest are blue.
1 ball is taken out of the bag and replaced, a second ball is then drawn from the bag.
Dannielle then draws a tree diagram shown below to represent this information.
x and y both represent fractions
2(a) Give the fraction represented by x
ANSWER: Fraction
3/7
Workings:
3 out of the 7 balls are green
Marks = 1
2(b) Give the fraction represented by y
ANSWER: Fraction
4/7
4 out of the 7 balls are blue.
Question 3
Jenny is competing in two independent events at today’s sports day.
She will be competing in both the javelin and the 100m sprint.
The probability that she wins the javelin is 0.8
The probability that she wins the 100m sprint is 0.5
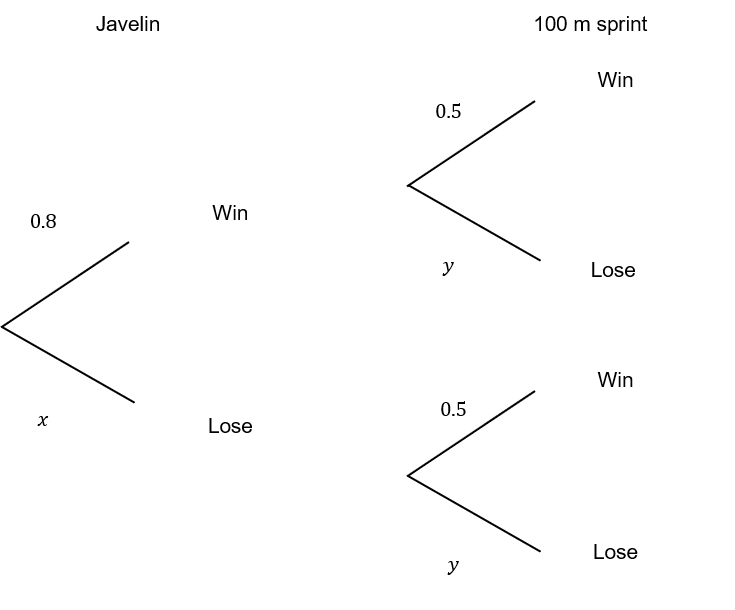
A tree diagram to represent this information is shown below.
2(a) Give the value of x and the value of y
Give your answer as decimals
ANSWER: Multiple answer
x = 0.2
y = 0.5
Workings:
x = 1 - 0.8 = 0.2
y = 1-0.5=0.5
Marks = 1
2(b) Calculate the probability that she loses both events.
Give your answer as a decimal.
ANSWER: Simple answer
0.1
Workings:
0.2\times0.5 = 0.1
Question 4
Layla-Mae want to work out the probability of rolling 3 fives in row.
To do this she draws the following tree diagram
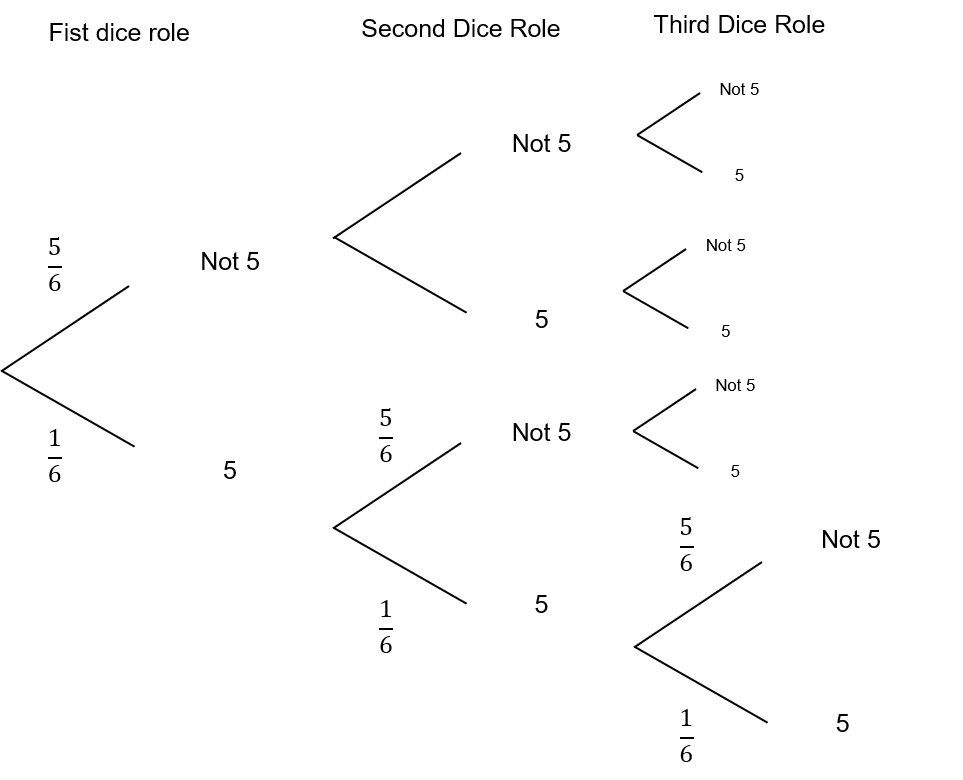
Using the tree diagram above, calculate the probability of rolling 3 fives in a row.
Give your answer as a fraction in its simplest form.
ANSWER: Fraction
1/216
Workings:
\dfrac{1}{6}\times \dfrac{1}{6} \times \dfrac{1}{6}=\dfrac{1}{216}Marks = 1
Question 5 (Was Question 3)
The probability of Ben completing his Maths homework on any night is \dfrac{1}{3}.
The probability that he completes his English homework is \dfrac{1}{4}.
These are both independent events.
3(a) Select the correct tree diagram to represent this information from the options below.
A:
B: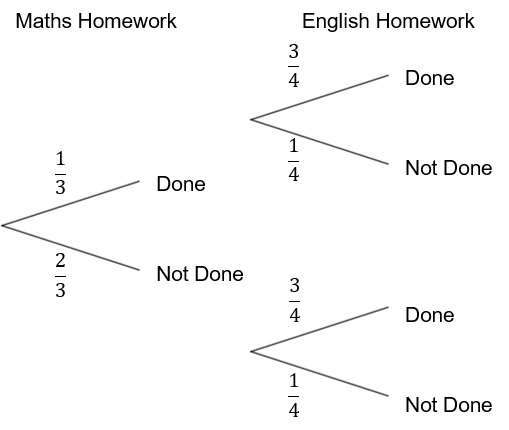
C: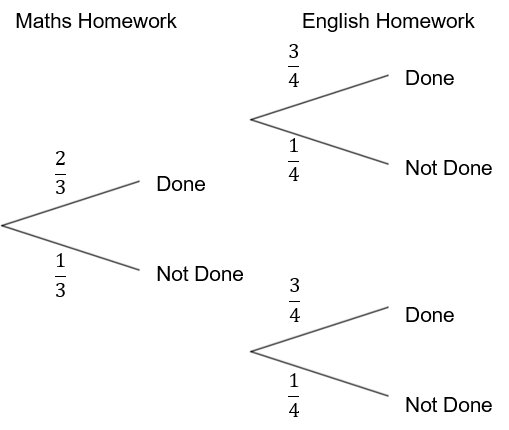
D: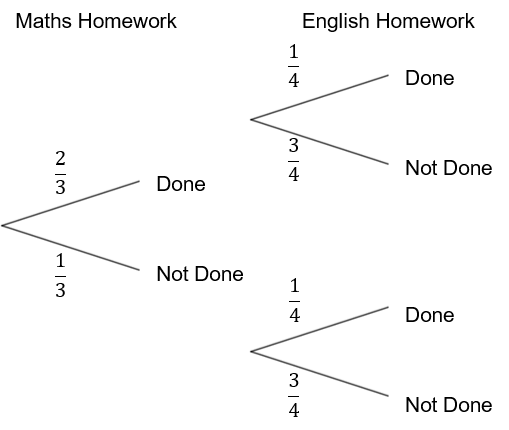
Answer: A
Workings:
Probabilities add up to 1 for each event. Treating each event separately gives,
\text{P( Maths not done)}= 1 - \dfrac{1}{3}
\text{P(English not done)}=1-\dfrac{1}{4}
Marks = 3
3(b) Calculate the probability that Ben completes both pieces of homework.
Give your answer as a fraction in its simplest form.
ANSWER: Fraction
Answer: \dfrac{1}{12}
Workings:
\text{P(both done)} = \dfrac{1}{3}\times\dfrac{1}{4}=\dfrac{1}{12}
Marks = 1
3(c) Calculate the probability that Ben completes exactly one piece of homework.
Give your answer as a fraction in its simplest form.
ANSWER: Fraction
Answer: \dfrac{5}{12}
Workings:
\text{P(Maths done, English not done)}=\dfrac{1}{3}\times\dfrac{3}{4}=\dfrac{1}{4}
\text{P(Maths not done, English done)}=\dfrac{2}{3}\times\dfrac{1}{4}=\dfrac{1}{6}
\text{P(only one piece of homework done)}=\dfrac{1}{4}+\dfrac{1}{6}=\dfrac{5}{12}
Marks = 2
Question 6 (Was Question 2)
Katie completes two events at her school sports day, hurdles and javelin.
2(a) Complete the probability tree diagram below showing the probabilities of Katie winning each event.
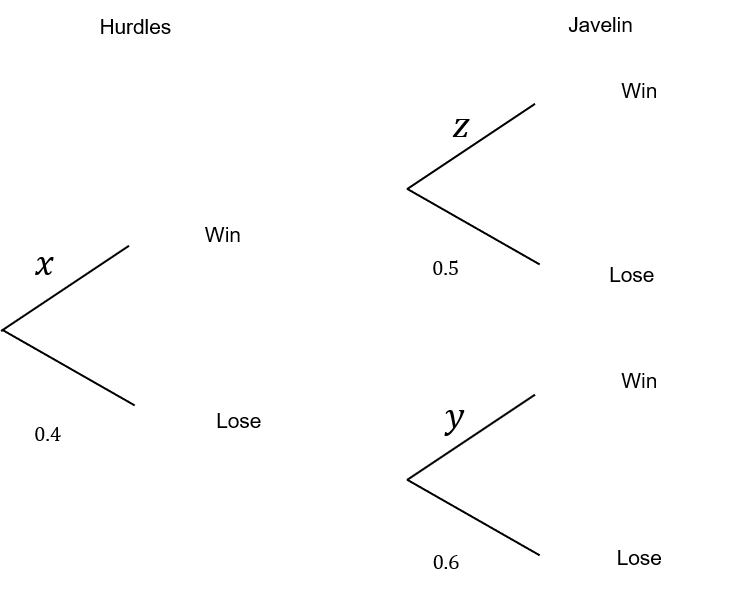
ANSWER: Multiple Answers (Type 1)
Answer: x=0.6 y=0.4 z=0.5
Workings:
Probabilities must add up to 1 for each event. So,
x=1-0.4=0.6
y=1-0.6-0.4
z=1-0.5=0.5
Marks = 2
2(b) Calculate the probability that Katie wins one event and loses the other.
Give your answer as a decimal.
ANSWER: Simple Text Answer
Answer: 0.46
\text{P(Win then Loss)}=0.6\times0.5=0.3
\text{P(Loss then Win)}=0.4\times0.4=0.16
\text{P(one Win and one Loss)}=0.3+0.16=0.46
