Question 1:
23 boys and 22 girls take a maths test.
The mean mark for the boys was 44.
The mean mark for the girls was 42.
Find the mean mark for all 45 students.
Give your answer to 1 decimal place.
ANSWER: Simple
Answer: 43.0
Workings:
Total mark for boys =23\times44=1012
Total mark for girls =22\times42=924
Total mark for all students =1012+924=1936
Total number of students =22+23=45
Mean =1936 \div 45=43.0 (1 dp)
Question 2:
Consider the following set of numbers
1,\quad 20,\quad 15,\quad 8,\quad 7,\quad 8,\quad 7,\quad 11,\quad 11,\quad 1,\quad 8
2(a) Calculate the mean to 1 decimal place.
ANSWER: Simple
Answer: 8.8
Workings:
(1+20+15+8+7+8+7+11+11+1+8)\div 11=8.8
Marks = 1
2(b) Give the value of the mode
ANSWER: Simple
Answer: 8
Workings:
8 appears most often in the set.
Marks = 1
2(c) Give the value of the median
ANSWER: Simple
Answer:8
Workings:
Putting the numbers in order:
1,1,7,7,8,8,8,11,11,15,20
There are 11 numbers in total (n)
The median is given by the \dfrac{n+1}{2} value which in this case is the \dfrac{12}{2}=6^{\text{th}} value, which is 8.
Marks = 1
2(d) Find the range
ANSWER: Simple
Answer: 19
Workings:
The range is the highest value – lowest value which is 20-1=19
Marks = 1
Question 3:
James has a number of 6 kg sacks of carrots, and a number of 16 kg sacks of carrots.
The mean weight of the sacks of carrots is 12 kg.
What is the least number of 6 kg and 16 kg sacks of carrots that James has?
ANSWER: Multiple answers
Answers:
6 kg: 2
16 kg: 3
Workings:
There are 2 methods to solve this question.
Method 1- Trial and Improvement
2\times6 kg +2\times16 kg =44, \quad 44\div4 \ne 12
3\times6 kg +2\times16 kg =50, \quad 50\div5 \ne 12
2\times6 kg +3\times16 kg =60, \quad 60\div5 = 12
So there are two 6 kg bags and three 16 kg bags
Method 2 – Algebra
Setting up an expression where x= the number of 6 kg bags and y= the number of 16 kg bags:
\dfrac{6x+16y}{x+y}=12
6x+16y=12x+12y
6x=4y
3x=2y
y-\dfrac{3x}{2}
If x=1,y=\dfrac{3}{2} – you cannot have half a sack of carrots so move on to the next value
If x=2, y=3 – hence there two 6 kg bags and three 16 kg bags.
Question 4:
Christopher has seven rabbits in his garden.
Their weights, in kg, are listed below.
1.1, \quad 1.9, \quad 1.5, \quad 1.3, \quad 2.0, \quad 1.3, \quad 1.7
4(a) Calculate the mean.
Give your answer to 1 decimal place.
ANSWER: Simple
Answer: 1.5 kg
Workings:
(1.1+1.9+1.5+1.3+2.0+1.3+1.7)\div7=1.5Marks = 1
4(b) Give the value of the mode.
ANSWER: Simple
Answer: 1.3
Workings:
1.3 appears most often in the set.
Marks = 1
4(c) Give the value of the median.
ANSWER: Simple
Answer: 1.5 kg
Workings:
Ordering the weights:
1.1, 1.3, 1.3, 1.5, 1.7, 1.9, 2.0
There are 7 values (n).
The median is given by the \dfrac{n+1}{2} value which in this case is the \dfrac{8}{2}=4^{\text{th}} value, which is 8. Hence the median is 1.5 kg.
4(d) Calculate the range.
ANSWER: Simple
Answer: 0.9 kg
Workings:
Range =2.0-1.1=0.9 kg
Marks = 1
4(e) Two of the rabbits are put in their hutch.
The average weight of the remaining five rabbits is now 1.6 kg.
Find the combined weight of the two rabbits that were put in their hutch.
ANSWER: Simple
Answer: 2.8 kg
Workings:
Let x be the combined weight of the two rabbits that were removed.
The previous combined weight of the 7 rabbits was 1.1+ 1.3+ 1.3+ 1.5+ 1.7+ 1.9+ 2.0=10.8
Setting up an expression:
\dfrac{10.8-x}{5}=1.6
10.8-x=8
x=2.8
Marks = 3
Question 5:
Sarah earns £8.43 an hour. She thinks that most of her friends are paid more.
Here is a list of how much her friends earn per hour.
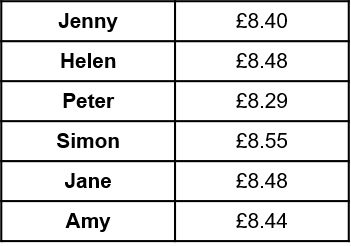
5(a) Calculate the mean hourly rate of her friends’ pay.
ANSWER: Simple
Answer: £8.44
Workings:
(8.40+8.48+8.29+8.55+8.48+8.44)=50.64 50.64\div 6 = 8.44Marks = 1
5(b) What is the mode hourly rate of her friends’ pay?
ANSWER: Simple
Answer: £8.48
Workings:
£8.48 is the only value that appears more than once.
Marks = 1
5(c) What is the median hourly rate of her friends’ pay?
ANSWER: Simple
Answer: £8.46
Workings:
Putting the hourly rates of pay in order:
8.29, 8.40, 8.44, 8.48, 8.48, 8.55
There are 6 values (n).
The median is given by the \dfrac{n+1}{2} value which in this case is the \dfrac{7}{2}=3.5^{\text{th}} value, i.e. the midpoint of the 3^{\text{rd}} and 4^{\text{th}} value, which in this case is £8.46.
Marks = 1
5(d) Using your answers from 4(a)-(c), state whether Sarah is correct.
Select the correct statement below.
ANSWER: Multiple Choice
Answer: A
A: She is correct, because the mean, median and mode are all higher than her hourly pay rate.
B: She is wrong, because only the mean is higher but this is affected by outliers.
C: She is correct, but the median pay rate is lower than hers.
D: She is wrong, because neither the mean, median or mode are higher than her hourly pay rate.
Workings:
All three measures are higher than Sarah’s rate so she is correct. The mean is affected by outliers, but there are no real outliers in the list of values here.
Marks = 1
Question 6:
Jane recorded the time taken, in minutes, for her friends to complete a jigsaw (to the nearest minute).
The times taken are shown in the bar chart below.

6(a) Find the mean time taken to complete the jigsaw. Give your answer to 1 decimal place.
ANSWER: Simple
Answer: 4.5 minutes
Workings:
\dfrac{3+3+3+3+4+4+5+6+7+7}{10}=4.5Marks = 3
6(b) Find the range of times taken.
ANSWER: Simple
Answer: 4 minutes
Workings:
Range = 7-3=4
Marks = 1
Question 7:
Sally has 4 cards taken from a deck of 10 cards labelled 1 to 10, as shown below:

The range of the cards is 8.
The median of the cards is 6.
The mean of the cards is 5.5.
7(a) Sally already knows the number 4 is not one of her three cards as it is missing from the deck.
Find the 3 missing numbers.
ANSWER: Multiple choice
A: 5, 7, 9
B: 5, 6, 10
C: 3, 8, 10
D: 2,9,10
Answer: A
Workings:
Median:
The median is 6, which is the \dfrac{n+1}{2}=\dfrac{4+1}{2}=2.5^{\text{th}} value. So the median is halfway between the 2^{\text{nd}} and 3^{\text{rd}} value. Therefore,
\dfrac{2^{\text{nd}}\text{ value}+3^{\text{rd}}\text{ value}}{2}=6
So,
2^{\text{nd}}\text{ value}+3^{\text{rd}}\text{ value}=12
So the sum of the second and third cards is 12
Mean:
The mean is 5.5 so the sum of all 4 cards is 4\times5.5=22
One card is the number 1, so the three missing cards must sum to 21
Given that two of the values sum to 12, the other missing card must be 9.
Range:
The remaining two cards sum to 12. This gives the following possibilities:
2 \text{ and } 10
4 \text{ and } 8
5 \text{ and } 7
The missing cards cannot be 2 and 10, as having the number 10 would give a range of 9. The number 4 is missing from the deck so the missing cards cannot be 4 and 8. Thus, the missing cards are 5 and 7.
The three missing cards are therefore: 5, 7, 9
Marks = 3
7(b) Sally adds one more card to the set.
The median of all 5 cards is 6.
What number card did she add?
ANSWER: Simple
Answer: 6
Workings:
The median is the \dfrac{n+1}{2}=\dfrac{5+1}{2}=3^{\text{rd}} value, i.e. the 3^{\text{rd}} card, therefore the card is 6.
Question 8:
A school is investigating how much their students use social media.
They gave their results, measured in minutes, in the table below.
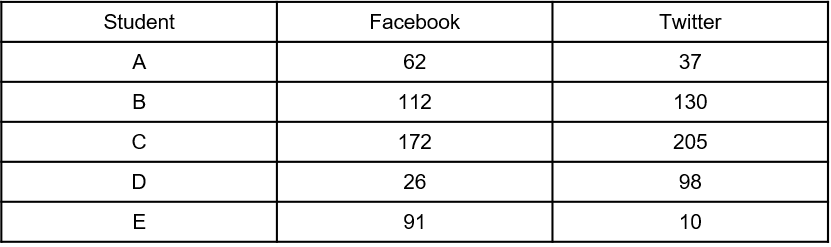
Work out the difference in the mean time spent on Facebook and Twitter.
Give your answer in minutes and seconds
ANSWER: Multiple answers
Answers:
Mins = 3
Seconds = 24
Workings:
Facebook mean =(62+112+172+26+91)\div5=92.6 mins =92 mins 36 seconds
Twitter mean =(37+130+205+98+10)\div=5=96 miins
Difference = 3 mins 24 seconds
Question 9
The height of 13 students, in cm, are listed below.
141,\quad 130, \quad 135, \quad 144, \quad 130, \quad 152, \quad 145, \\ 140, \quad 153, \quad 160, \quad 180, \quad 120, \quad 134
9(a) Find the range of the students heights
ANSWER: Simple
Answer: 60 cm
Workings:
Range =180-120=60 cm
Marks = 1
9(b) Find the median of the students heights
ANSWER: Simple
Answer: 141 cm
Workings:
Putting the heights in order:
120, 130, 130, 134, 135, 140, 141, 144, 145, 152, 153, 160, 180
The median is given by the \dfrac{13+1}{2}=7^{\text{th}} value, which is 141 cm.
Marks = 1
9(c) Find the mode of the students heights
ANSWER: Simple
Answer: 130 cm
Workings:
The only height that appears more than once is 130 cm
Marks = 1
9(d) Find the mean of the students heights, giving your answer to 3 significant figures.
ANSWER: Simple
Answer: 143 cm
Workings:
Sum of all heights = 120+ 130+ 130+ 134+ 135+ 140+ 141+ 144+ 145 +152+ 153+ 160+ 180=1864 cm
Mean =1864 \div 13= 143 cm (3 sf)
