PAPER 10A
QUESTION 1 [2 marks]
What is \dfrac{14}{5} - \dfrac{8}{3} ?
Give your answer as an improper fraction in its simplest form.
Answer type: Fraction
ANSWER: \dfrac{2}{15}
WORKING:
\dfrac{14}{5} - \dfrac{8}{3}= \bigg(\dfrac{14}{5}\times\dfrac{3}{3}\bigg) - \bigg(\dfrac{8}{3}\times\dfrac{5}{5}\bigg)=\dfrac{42}{15}-\dfrac{40}{15}=\dfrac{2}{15}
QUESTION 2 [1 mark]

Describe the nature of the correlation shown in the scatter graph.
Answer type: Multiple choice type 1
A: Weak negative correlation
B: Weak positive correlation
C: Strong positive correlation
D: No correlation
ANSWER: A
QUESTION 3 [3 marks]
The triangle ABC is an isosceles triangle.
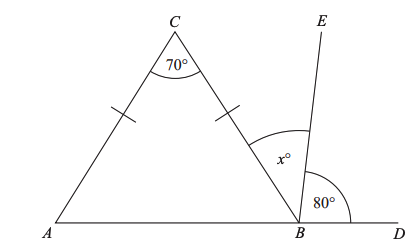
Work out the value of angle x
Answer type: Simple text answer
ANSWER: x= 45 \degree
WORKING:
As triangle ABC is an isosceles triangle, the two angles \angle ABC and \angle BAC are equal.
\angle ABC = \dfrac{180 - 70}{2}=55\degree
x= 180 - 80 - 55 = 45\degree
QUESTION 4 [1 mark]
Work out 5 \times (2 + 1) + 4
Simple text answer
ANSWER: 19
WORKING:
5 \times (2 + 1) + 4= 5\times3+4=15+4=19
QUESTION 5 [2 marks]
In a drawer there are,
6 blue pairs of socks, 9 yellow pairs of socks, 4 black pairs of socks and 5 white pairs of socks.
A pair of socks is taken from the drawer at random.
What is the probability that the pair of socks chosen is blue or black?
Give your answer as a fraction in simplest form.
Answer type: Fraction
ANSWER: \dfrac{5}{12}
WORKING:
Total number of socks =6+9+4+5=24
Probability that pair is blue or black = \dfrac{6+4}{24} = \dfrac{10}{24}=\dfrac{5}{12}
QUESTION 6 [2 marks]
The price of a chocolate box has increased by 25\%. The box of chocolate now costs £17.25
How much did it cost originally?
Answer type: Simple text answer
ANSWER: £13.80
WORKING:
£17.25 \div 1.25 = £13.80
QUESTION 7 [1 mark]

What 3D shape can be created with this net?
Answer type: Multiple choice type 1
A: Cube
B: Frustum
C: Square-based pyramid
D: Square
ANSWER: A
QUESTION 8 [3 marks]
Christopher has seven rabbits in his garden. Their weights in kilograms are listed below.
1.1, 1.9, 1.5, 1.3, 2.0, 1.3, 1.7
What is the difference between the mean of the weight of the rabbits and the median weight of the rabbits?
Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 0.04 kg
WORKING:
Total = 1.1 + 1.9 + 1.5 + 1.3 + 2.0 + 1.3 + 1.7 = 10.8
Mean = 10.8 \div 7 = 1.54 kg
For the median, order the numbers from smallest to largest:
1.1, 1.3, 1.3, 1.5, 1.7, 1.9, 2.0
The median is the \dfrac{n+1}{2} = \dfrac{8}{2} = 4th value from the ordered list
Median = 1.5 kg
Difference = 1.54 - 1.5 = 0.04kg
PAPER 10B
QUESTION 1 [4 marks]
Jordan finishes college at 16:30 h.
He walks to his mum’s work 0.15 miles away, at a speed of 2 km/h.
He waits there 7 minutes for his mum to finish work before she drives them both 7 km back home at an average speed of 16.25 miles per hour.
1 mile = 1.6 km
What time does Jordan arrive home, to the nearest minute?
Answer type: Multiple choice type 1
A: 17:00
B: 16:56
C: 17:07
D: 16:53
ANSWER: A
WORKING:
0.15 miles = 0.15 \times 1.6 = 0.24 km
16.25 miles = 16.25 \times 1.6 = 26 km, so 16.25 mph = 26 km/h
Walk: \text{T} = \dfrac{\text{D}}{\text{S}} = \dfrac{0.24}{2} = 0.12 hours = 7.2 minutes
Driving: \dfrac{7}{26} = 0.2692 hours \approx 16.2 minutes
Total: 7.2 + 7 + 16.2 = 30.4 \approx 30 minutes
Adding 30 minutes to 16:30 gives an arrival time of 17:00
QUESTION 2 [3 marks]
A conservation group try to estimate the population of different types of tress that are found in a nearby forest:
\dfrac{1}{18} of the trees are oak
\dfrac{2}{9} of the trees are beech
and \dfrac{1}{4} of the trees are pine.
The group estimates there are 720 trees in the forest. How many of these trees are not oak or pine?
Answer type: Simple text answer
ANSWER: 500
WORKING:
\dfrac{1}{18} are oak hence \dfrac{1}{18} \times 720 = 40 of the trees are oak.
\dfrac{1}{4} are pine hence \dfrac{1}{4} \times 720 = 180 of the trees are pine.
There are a total of 40+180=220 oak and pine trees.
So 720 - 220 = 500 trees in the forest are not oak or pine.
QUESTION 3 [4 marks]
A carpenter plans to carve a doorstop out of a block of wood that has a density of 5.24 g/cm^3.
Calculate the mass of the doorstop, in g, if this is the design:

Answer type: Simple text answer
ANSWER: 78.6 g
WORKING:
Volume = (\dfrac{1}{2} \times 3 \times 5) \times 2 = 15 cm^3
Mass = \text{Density}\times\text{Volume}=5.24 \times 15 = 78.6 g
QUESTION 4 [5 marks]
A school is purchasing stationary before the new term commences. The school requires 126 pencils, 48 books and 80 crayons.
The school can choose to purchase the stationary from Shop A or Shop B.

How much will the school save in total by choosing the cheapest shop to buy all of the stationary?
Answer type: Simple text answer
ANSWER: £7.95
WORKING:
SHOP A:
126 pencils with the promotion of 5 for the price of 4, means the school pays for \dfrac{126}{5} \times 4 = 100.8 = 101 pencils.
Cost = 101\times £0.25=£25.25
48 books with the promotion of 8 for the price of 7, means the school pays for \dfrac{48}{8} \times 7 = 42 books.
Cost = 42\times\text{£}2.00=\text{£}84.00
80 crayons with the promotion of 30\% off the price, means the school pays £0.90 \times 0.7 = \text{£}0.63 per crayon.
Cost = 80\times \text{£}0.63=\text{£}50.40
Total cost = \text{£}25.25+\text{£}84.00+\text{£}50.40=\text{£}159.65
SHOP B:
126 pencils in packs of 10 means the school needs \dfrac{126}{10} = 12.6 = 13 packs of pencils.
13 packs of pencils with the promotion of 20\% off the price, means the school pays £3.00 \times 0.8 = £2.40 per pack.
Cost = 13 \times £2.40 = £31.20
48 books in packs of 5 means the school needs \dfrac{48}{5} = 9.6 = 10 packs of books.
10 packs of books with the promotion of 3 for the price of 2, means the school pays for \dfrac{10}{3} \times 2 = 6.66... = 7 packs.
Cost = 7 \times £11.50 = £80.50
80 crayons in packs of 20 means the school needs \dfrac{80}{20} = 4 packs of crayons.
4 packs of crayons with the promotion of \dfrac{1}{3} off the price, means the school pays £15.00 \times \dfrac{2}{3} = £10.00 per pack.
Cost = 4 \times £10.00 = £40.00
Total cost = £31.20 + £80.50 + £40.00 = £151.70
Shop B is the cheapest shop to buy all of the stationary.
Difference = £159.65 - £151.70 = £7.95
QUESTION 5 [1 mark]
Choose the correct plot of the coordinate (10,3) on the graph below.

Answer type: Multiple choice type 1
A:

B:

C:

D:
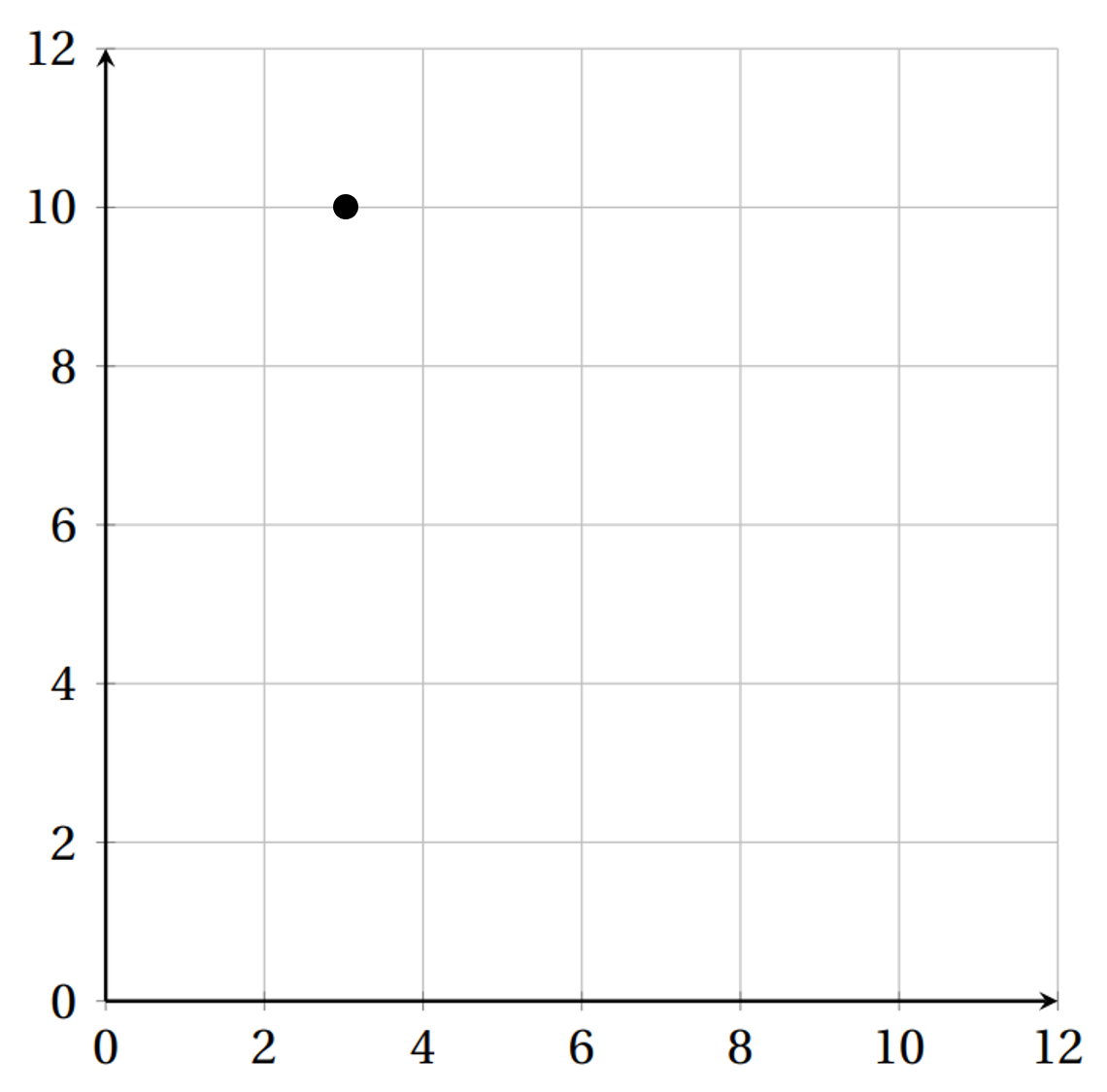
ANSWER: C
QUESTION 6 [5 marks]
The diagram below shows a representation of a small USB drive consisting of two cuboids, ABCDEFGH and IJKLMNOP attached together.
AC=12 mm, BH=3 mm, GF=9 mm, IL=3 mm, KO=1 mm, IJ=e

Calculate the total surface area of the USB drive, if e = 2.5 mm
Answer type: Simple text answer
ANSWER: 362 mm^2
WORKING:
Big cuboid:
(12\times3)\times2=72,
(9\times12 )\times2=216,
(3\times9 )\times2=54
Total =342 mm^2
Small cuboid:
(3\times 2.5)\times2=15,
(1\times 2.5)\times2=5,
(3\times1)\times2=6
Total =15+5+6 = 26 mm^2
Overlapping surface area =(3\times1)\times2=6 mm^2
Total Area of USB = 342+26-6=362 mm^2
QUESTION 7 [3 marks]
Edith starts on a salary of £23800 and gets a raise of 6\% every year.
She gets 20\% deducted from her salary each year due to tax.
What will be her annual income after tax in 2 years time?
Give your answer to the nearest pound.
Answer type: Simple text answer
ANSWER: £21393
WORKING:
Year 1: £23800 \times 1.06 = £25228
Year 2: £25228 \times 1.06 = £26741.68
Income after tax = £26741.68 \times 0.8 = £21393 (nearest pound)
QUESTION 8 [4 marks]
The table below shows some information about the ages of football fans in a stadium.

Estimate the mean age of football fans in the stadium.
Answer type: Simple text answer
ANSWER:
WORKING:
Calculate the midpoint of each group, and write the results in a new column.
Multiply the frequency by the midpoint for each group, and write the results in a new column.
Add up the frequency column to find the total number of people in the stadium.
Add up the ‘frequency \times midpoint’ column.
See the table below.

Estimated mean age = \dfrac{913138}{23402} = 39.02 (2 dp)
QUESTION 9 [2 marks]
The probability of a badminton player winning a match is \dfrac{1}{4}
The player is competing in two matches over the weekend.
What is the probability of the player winning neither of those games?
Give your answer as a decimal.
Answer type: Simple text answer
ANSWER: 0.5625
WORKING:
Probability of not winning = 1 - \dfrac{1}{4} = \dfrac{3}{4} = 0.75
Probability of not winning both games = 0.75\times 0.75 = 0.5625
QUESTION 10 [1 mark]
A car motorcycle firm charges a fixed £50 fee then charges per mile driven.

Using the conversion graph, how much would it cost to drive 300 miles?
Answer type: Simple text answer
ANSWER: £170
WORKING:

QUESTION 11 [3 marks]
The table below shows figures for the number of ticket sales at a local attraction on one day.

The ratio of student tickets to other concession tickets sold was 5:2
What percentage of the total ticket sales on this day were student tickets?
Give your answer to 1 decimal place.
Answer type: Simple text answer
ANSWER: 7.8 \%
WORKING:
Total parts in ratio = 5+2 = 7
1 part = 63 \div 7 = 9
Student tickets sold = 5 \times 9 = 45
Total tickets sold = 356 + 157 + 63 = 576
Percentage of total tickets sold that were student tickets = \dfrac{45}{576} \times 100 = 7.8 \% (1 dp)
QUESTION 12 [2 marks]

You are given that \pi = 3.14
Find the area of the circle.
Give your answer to the nearest whole number.
Answer type: Simple text answer
ANSWER: 201 cm^2
WORKING:
Area = \pi r^2 = 3.14 \times 8^2=201 cm^2 (nearest whole number)
QUESTION 13 [3 marks]
Peter buys a new car. He uses the following formula to calculate its horsepower (hp).
\text{Horsepower (HP)} = \dfrac{\text{Torque in ft/lb} \times \text{RPM}}{5252}
Calculate the horsepower of the car, when it has
Torque in \text{Nm} = 598
\text{RPM} = 20001 \text{ ft/lb} = 1.356 \text{ Nm}
Give your answer to the nearest whole number.
Answer type: Simple text answer
ANSWER: 168 hp
WORKING:
Torque in \text{ft/lb} = 598 \div 1.356 = 441.002...
Horsepower = \dfrac{441.002... \times 2000}{5252} = 168 hp
QUESTION 14 [2 marks]
A 500 credit banknote in from a board game is displayed below.

Find the perimeter of the banknote.
Answer type: Simple text answer
ANSWER: 39.8 cm
WORKING:
Perimeter =14.3+14.3+5.6+5.6 =39.8 cm
QUESTION 15 [3 marks]
16 students need to drink 4.25 litres of water between them over the course of the day.
How much water would be needed for 27 students?
Assume that all students drink the water at the same rate.
Give your answer in litres, to 2 decimal places.
Answer type: Simple text answer
ANSWER: 7.17 litres
WORKING:
4.25 litres \div \, 16 students = 0.265625 litres per student
for 27 students they would need 27 \times 0.265625 = 7.17 litres (2 dp)
