PAPER 8A

 

QUESTION 1 [1 mark]

Given that 28×1356=3796828\times1356= 37968

Calculate the following: 2.8×1.3562.8 \times 1.356

 

Answer type: Simple text answer

ANSWER: 3.7968

 

 

QUESTION 2 [2 marks]

In a drawer there are 66 blue pairs of socks, 99 yellow pairs of socks, 44 black pairs of socks and 55 white pairs of socks.

A pair of socks is taken from the drawer at random.

What is the probability that the pair of socks chosen is white?

Give your answer as a fraction in simplest form.

 

Answer type: Fraction

ANSWER: 524\dfrac{5}{24}

WORKING:

Total number of socks =6+9+4+5=6+9+4+5

Number of white socks =5=5

Probability =524=\dfrac{5}{24}

 

 

QUESTION 3 [1 mark]

Here are six numbers:

0.42,    36,    39,    −1.27,    0.55,    2100.42, \,\,\,\, \dfrac{3}{6}, \,\,\,\, \dfrac{3}{9}, \,\,\,\, -1.27, \,\,\,\, 0.55, \,\,\,\, \dfrac{2}{10}

 

Order the numbers from least to most.

 

Answer type: Multiple choice type 1

A: −1.27,210,    39,    0.42,    36,    0.55-1.27, \dfrac{2}{10}, \,\,\,\, \dfrac{3}{9}, \,\,\,\, 0.42, \,\,\,\, \dfrac{3}{6}, \,\,\,\, 0.55

B: −1.27,210,    39,    36,    0.42,    0.55-1.27, \dfrac{2}{10}, \,\,\,\, \dfrac{3}{9}, \,\,\,\, \dfrac{3}{6}, \,\,\,\, 0.42, \,\,\,\, 0.55

C: 210,    39,    0.42,    36,    0.55,    −1.27\dfrac{2}{10}, \,\,\,\, \dfrac{3}{9}, \,\,\,\, 0.42, \,\,\,\, \dfrac{3}{6}, \,\,\,\, 0.55, \,\,\,\, -1.27

D: 0.55,36,    0.42,    39,    210,    −1.270.55, \dfrac{3}{6}, \,\,\,\, 0.42, \,\,\,\, \dfrac{3}{9}, \,\,\,\, \dfrac{2}{10}, \,\,\,\, -1.27

 

 

QUESTION 4 [2 marks]

If 200200 grams of one ingredient is used in a recipe, which calls for a ratio of 4:74: 7 with a second ingredient, how much of the second ingredient is needed?

 

Answer type: Simple text answer

ANSWER: 350 grams

WORKING:

44 parts for ingredient one, 77 parts for the second ingredient.

200÷4=50200\div4=50

50×7=35050\times7=350 grams

 

 

QUESTION 5 [2 marks]

A student is been sponsored to cycle a distance of 5050 kilometres. He travels 2020 miles. How many kilometres more does he need to travel to reach his 5050 kilometre target? You may use the approximation that 11 mile is 1.61.6 kilometres.

 

Answer type: Simple text answer

ANSWER: 18 km

WORKING:

2020 miles × 1.6=32\times \, 1.6=32 km

50−32=1850-32=18 km

 

 

QUESTION 6 [2 marks]

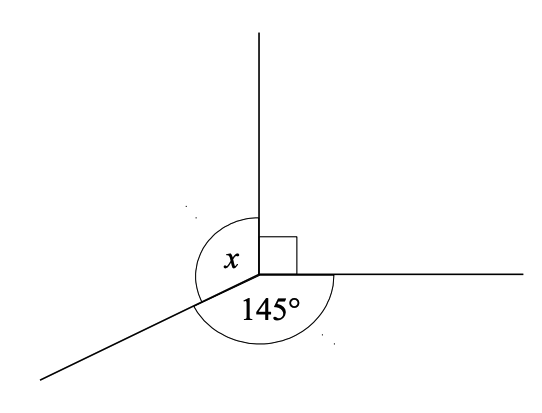
Find the missing angle labelled xx

 

Answer type: Simple text answer

ANSWER: x=x= 125 °\degree

WORKING:

x=360−90−145=125°x = 360 - 90 - 145 =125\degree

 

 

QUESTION 7 [3 marks]

A tin of biscuits has 36 assorted biscuits.

The probability that a biscuit selected at random has a chocolate coating on it is 0.75

How many biscuits do not have chocolate on them?

 

Answer type: Simple text answer

ANSWER: 9 biscuits

 

WORKING:

1−0.75=0.25 1-0.75 =0.25 0.25×36=90.25 \times 36 = 9

 

 

 

QUESTION 8 [2 marks]

Iron has a density of 7.87.8 g/cm3^3

Calculate the mass of a 3.23.2 cm3^3 lump of iron.

 

Answer type: Simple text answer

ANSWER: 24.96 g

WORKING:

Mass=Density×Volume=(7.8\text{Mass}=\text{Density} \times \text{Volume}= (7.8 g/cm3)×(3.2^3) \times (3.2 cm3)=24.96^3) =24.96 g

 

 

PAPER 8B

 

QUESTION 1 [2 marks]

Calculate the following: (4+22)2−2(4+2^2)^2-2

 

Answer type: Simple text answer

ANSWER: 62

WORKING:

(4+22)2−2=(4+4)2−2=82−2=64−2=62(4+2^2)^2-2=(4+4)^2-2=8^2-2=64 - 2 = 62

 

 

QUESTION 2 [4 marks]

Sarah has started reading a new book.

On Saturday she reads 215\dfrac{2}{15} of the book.

On Sunday she reads a further 13\dfrac{1}{3} of the total number of pages in the book.

On Monday she reads another 15\dfrac{1}{5} of the total number of pages in the book.

On Tuesday she finishes the book.

The ratio she read on Tuesday morning to Tuesday evening was 1:21:2

What fraction of the book did she read on Tuesday evening?

Write your answer in its simplest form.

 

Answer type: Fraction

ANSWER: 29\dfrac{2}{9}

WORKING:

215+13+15=215+(13×55)+(15×33) \dfrac{2}{15}+\dfrac{1}{3} + \dfrac{1}{5}= \dfrac{2}{15}+ \bigg(\dfrac{1}{3} \times \dfrac{5}{5} \bigg) + \bigg(\dfrac{1}{5}\times \dfrac{3}{3} \bigg)

215+515+315=1015\dfrac{2}{15}+\dfrac{5}{15}+\dfrac{3}{15}=\dfrac{10}{15}

1−1015=131-\dfrac{10}{15}=\dfrac{1}{3}

 

There are 1+2=31+2=3 parts in the ratio

11 part =13÷3=19= \dfrac{1}{3} \div 3 = \dfrac{1}{9}

She read 19×2=29\dfrac{1}{9} \times 2 = \dfrac{2}{9} on Tuesday evening

 

 

QUESTION 3 [3 marks]

The diagram below shows a rectangle with a section missing.

Work out the area of the shape.

 

Answer type: Simple text answer

ANSWER: 15275 cm2^2

WORKING:

Area of big rectangle =120×195=23400= 120 \times 195 = 23400 cm2^2

Area of missing rectangle =(120−55)×(195−70)=65×125=8125= (120-55) \times (195 - 70) = 65 \times 125 = 8125 cm2^2

Area =23400−8125=15275= 23400 - 8125 = 15275 cm2^2

 

 

QUESTION 4 [3 marks]

The cost of printing for students is given as:

Cost in pence=4×number of black and white pages+10×number of colour pages\text{Cost in pence} = 4 \times \text{number of black and white pages} + 10 \times \text{number of colour pages}

 

The cost of binding a booklet of less than 5050 pages costs £2£2

The cost of binding a booklet of 5050 pages or more costs £2£2 plus 55p per page.

Work out how much a booklet of 4545 black and white pages, and 1515 colour pages will cost to print and bind.

Give your answer in pounds.

 

Answer type: Simple text answer

ANSWER: £5.80

WORKING:

Print cost =Cost in pence=4×45+10×15=330p=£3.30= \text{Cost in pence} = 4 \times 45 + 10 \times 15=330\text{p}=£3.30

Total number of pages =45+15=60= 45 + 15 = 60

Cost of binding =200+10×5=250p=£2.50= 200 + 10 \times 5 = 250 \text{p} = £2.50

Total cost =£3.30+£2.50=£5.80= £3.30 + £2.50 = £5.80

 

 

QUESTION 5 [3 marks]

The diagram below shows a quarter-circle with radius 44 cm

 

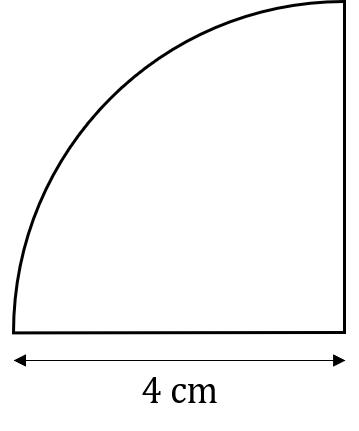
You are given that π=3.14\pi = 3.14

Calculate the perimeter of the quarter-circle.

Give your answer to 22 decimal places.

 

Answer type: Simple text answer

ANSWER:

WORKING:

Curved edge =14×2π×r=14×2×3.14×4=6.28= \dfrac{1}{4} \times 2 \pi \times r = \dfrac{1}{4} \times 2 \times 3.14 \times 4 = 6.28 cm

Perimeter =6.28+4+4=14.28= 6.28 + 4 + 4 = 14.28 cm

 

 

QUESTION 6 – here

A high street shop records the number of days it rains in a month and the number of umbrellas they sell.

 

Question 6(a) [2 marks]

A scatter graph is plotted to show the relationship between the number of rainy days in a month and the number of umbrellas sold.

Choose the correct plot.

 

Answer type: Multiple choice type 1

A:

B:

C:

D:

 

ANSWER: A

 

 

Question 6(b) [1 mark]

Use the graph to estimate the number of whole umbrellas they will sell if it rains for 1010 days in a month.

 

Answer type: Simple text answer

ANSWER: 8

 

 

QUESTION 7 [4 marks]

A castle under siege has enough food for 300300 men for 9090 days.

After 4040 days, 150150 men have left the castle.

How long would the food last at the same rate?

 

Answer type: Simple text answer

ANSWER: 100 days

WORKING:

300300 men × 90\times \, 90 days of food = 27000= \, 27000 days worth of food for one person

300300 men × 40\times \, 40 days of food = 12000= \, 12000 days worth of food for one person used

1500015000 days of food ÷ 150\div \, 150 men = 100= \, 100 days worth of food left

 

 

QUESTION 8 [4 marks]

33 years ago, Rachel deposited £2200£2200 into a savings account that pays 1.5%1.5\% compound interest per year.

Now, 33 years later, she wants to use the money in her savings account to buy a moped worth £2300£2300

Can she afford to purchase the moped?

 

Answer type: Multiple choice type 1

A: Yes

B: No

ANSWER: A

WORKING:

Year 1: £2200×1.105=£2233£2200 \times 1.105 = £2233

Year 2: £2233×1.015=£2266.495£2233 \times 1.015 = £2266.495

Year 3: £2266.495×1.015=£2300.492425£2266.495 \times 1.015 = £2300.492425

 

Yes, she does have enough money, since she has £2300.49£2300.49 (nearest penny), and she needs £2300£2300

 

 

Question 9 [3 marks]

James wants to buy 33 pairs of shorts.

Four shops sell the shorts he wants.

 

 

Which shop provides the best value for money for 33 pairs of shorts?

 

Answer type: Multiple choice type 1

A: Shop A

B: Shop B

C: Shop C

D: Shop D

 

ANSWER: B

WORKING:

Shop A:

3×£15=£453 \times £15 = £45

£45×0.8=£36£45 \times 0.8 = £36

 

Shop B:

2×£17.50=£352 \times £17.50 = £35

 

Shop C:

3×£14=£423 \times £14 = £42

£42−£5=£37£42 - £5 = £37

 

Shop D:

3×£12=£363 \times £12 = £36

 

Shop B provides the best value for money.

 

 

QUESTION 10 [3 marks]

Ester buys a new pair of shoes. The shoe box measures 342342 mm × 253\times \, 253 mm × 121\times \, 121 mm.

What is the volume of the shoe box in cm3^3 ?

Give your answer to the nearest whole number.

 

Answer type: Simple text answer

ANSWER: 10470 cm3^3

WORKING:

Volume =34.2×25.3×12.1=10470= 34.2 \times 25.3 \times 12.1 = 10470 cm3^3 (nearest whole number)

 

 

QUESTION 11 [4 marks]

The following grouped frequency table shows the number of hours of vigorous exercise done by members of the general public in a week.

Estimate the mean number of hours of vigorous exercise done by members of the general public in a week.

Give your answer to 22 decimal places.

 

Answer type: Simple text answer

ANSWER: 3.59 hours

WORKING:

Find the midpoint of each group, and write them in a new column.

Then calculate frequency×midpoint\text{frequency} \times \text{midpoint} for each group, and write them in a new column.

Then, add up the frequency column, and add up the frequency×midpoint\text{frequency} \times \text{midpoint} column.

See the table below.

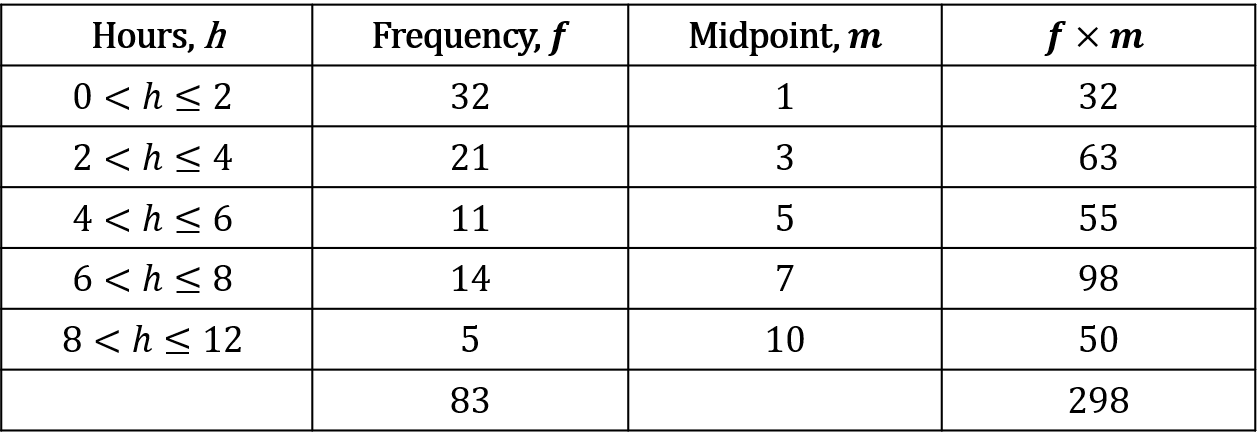
Estimated mean =29882=3.59= \dfrac{298}{82} = 3.59 hours (22 dp)

 

 

QUESTION 12 [1 mark]

The diagram shows the locations of several Towns.

Using the diagram, find the distance of Town B from Town I.

 

Answer type: Simple text answer

ANSWER: 30 km

 

QUESTION 13 [5 marks]

A runner participated in 55 runs using his old pair of trainers.

The table below shows their average speed in each run.

In the runner’s first run after using a new pair of trainers, he runs 55 km in 3535 minutes and 2424 seconds

11 mile =1.6=1.6 km

Calculate the percentage increase from the median speed of the 55 runs using the old trainers to the first run using the new trainers.

Give your answer to 22 decimal places.

 

Answer type: Simple text answer

ANSWER: 4.26 %\%

WORKING:

55 km =5÷1.6=3.125=5 \div 1.6 = 3.125 miles

3535 minutes and 2424 seconds =35.4= 35.4 minutes =0.59= 0.59 hours

Average speed using new trainers =3.125÷0.59=5.29661...= 3.125 \div 0.59 = 5.29661... mph

 

 

Order the 55 runs in order of speed, from slowest to fastest

4.94,5.03,5.08,5.16,5.324.94, 5.03, 5.08, 5.16, 5.32

 

The median is the middle value, which is 5.085.08 mph

 

 

Percentage increase =5.29661...−5.085.08×100=4.26%= \dfrac{5.29661... - 5.08}{5.08} \times 100 = 4.26 \%

 

 

QUESTION 14 [1 mark]

What 3D shape can be created with the net?

 

Answer type: Multiple choice type 1

A: Cone

B: Cylinder

C: Sphere

D: Tetrahedron

 

ANSWER: A

 

QUESTION 15 [2 marks]

Bethany hires a car for 33 days whilst on holiday.

The hire company costs €35.50€35.50 for the first day then €28.50€28.50 for each following day.

£1=€1.25£1 = €1.25

 

How much does she pay in total, in pounds (£)(£)?

 

Answer type: Simple text answer

ANSWER: £74

WORKING:

€35.50+(€28.50×2)=€92.50€35.50 + (€28.50\times2)=€92.50

92.50÷1.25=£7492.50 \div 1.25 = £74