PAPER 9A
QUESTION 1 [2 marks]
Write these fractions in order of size, starting with the smallest.
\dfrac{3}{8},\,\,\,\, \dfrac{2}{3},\,\,\,\, \dfrac{5}{6},\,\,\,\, \dfrac{3}{12}
Answer type: Multiple choice type 1
A: \dfrac{3}{12},\,\,\,\, \dfrac{3}{8},\,\,\,\, \dfrac{2}{3}, \,\,\,\, \dfrac{5}{6}
B: \dfrac{3}{12},\,\,\,\, \dfrac{3}{8},\,\,\,\, \dfrac{5}{6}, \,\,\,\, \dfrac{2}{3}
C: \dfrac{3}{8},\,\,\,\, \dfrac{3}{12},\,\,\,\, \dfrac{2}{3}, \,\,\,\, \dfrac{5}{6}
D: \dfrac{5}{6},\,\,\,\, \dfrac{2}{3},\,\,\,\, \dfrac{3}{8}, \,\,\,\, \dfrac{3}{12}
ANSWER: A
WORKING:
\dfrac{3}{8} = \dfrac{18}{48}\dfrac{2}{3} = \dfrac{32}{48}
\dfrac{5}{6} = \dfrac{40}{48}
\dfrac{3}{12} = \dfrac{12}{48}
Smallest to largest:
\dfrac{12}{48},\,\,\,\, \dfrac{18}{48},\,\,\,\, \dfrac{32}{48}, \,\,\,\, \dfrac{40}{48}
Smallest to largest in simplest form:
\dfrac{3}{12},\,\,\,\, \dfrac{3}{8},\,\,\,\, \dfrac{2}{3}, \,\,\,\, \dfrac{5}{6}
QUESTION 2 [1 mark]

Choose the front elevation of the 3D shape shown.
Answer type: Multiple choice type 1
A: 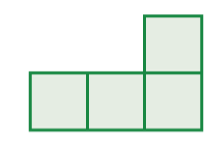 B:
B:  C:
C: 
ANSWER: A
QUESTION 3 [2 marks]
Six people sit around a table at a restaurant. Each of their ages are as follows:
23, 19, 20, 21, 24, 26
Find the median age of those sat at the table.
Answer type: Simple text answer
ANSWER: 22
The ages from smallest to largest: 19, 20, 21, 23, 24, 26
The median is the mean of the 3rd and 4th number, which is: \dfrac{21+23}{2}=22
QUESTION 4 [1 mark]
Calculate 6.284-3.691
Answer type: Simple text answer
ANSWER: 2.593
QUESTION 5 [2 marks]

Find the value of angle x\degree
Answer type: Simple text answer
ANSWER: x= 40 \degree
WORKING:
x = (180-100) \div 2 = 80 \div 2 = 40\degree
QUESTION 6 [2 marks]
Shaqil has some green and pink counters in a bag.
The ratio of green counters to total counters in the bag is 3:7
If Shaqil has 9 green counters, how many pink counters does he have?
Answer type: Simple text answer
ANSWER: 12
WORKING:
9 : 21There are 9 green counters and 21 in total
21 - 9 = 12 pink counters
QUESTION 7 [4 marks]
3 friends want to go for a hike. They each pack enough water to last for 7.25 hours. 2 more people join the hike, who each pack enough water to last 6 hours.
How long will the water last now if it is shared between everyone?
Assume that everyone consumes the water at the same rate.
Give your answer in hours.
Answer type: Simple text answer
ANSWER: 6.75 hours
WORKING:
(3 \times 7.25) + (2 \times 6) = 33.75 hours worth of water in total
33.75 \div 5 = 6.75 hours worth of water for 5 people
QUESTION 8 [1 mark]
The diagram shows the locations of several Towns.
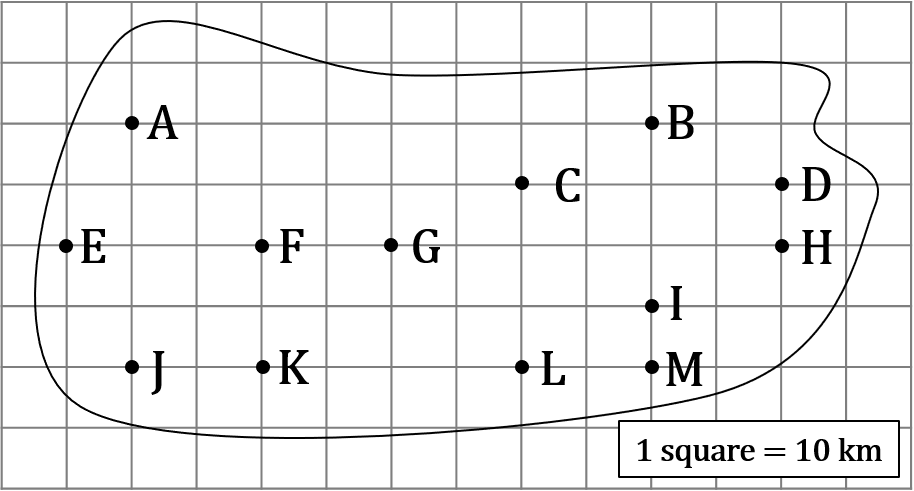
Using the diagram, find the distance of Town J from Town L.
Answer type: Simple text answer
ANSWER: 60 km
PAPER 9B
QUESTION 1 [3 marks]
Jenny is a race car driver, driving around a track.
She does 25 laps in 20 minutes, with an average speed of 144 km/h.
1 mile =1.6 km
Determine the distance travelled in one lap, in miles.
Answer type: Simple text answer
ANSWER: 1.2 miles
WORKING:
Time in Hours =\dfrac{20}{60}=\dfrac{1}{3}
Distance =144\times\dfrac{1}{3}=48 km
Distance per lap in km = 48\div25=1.92 km
Distance per lap in miles = 1.92 \div 1.6 = 1.2 miles
QUESTION 2 [2 marks]
Work out (3.75-0.28)^2-3.076
Give your answer as a decimal rounded to 2 decimal places.
Answer type: Simple text answer
ANSWER: 8.96
WORKING:
3.47^2 - 3.076 = 12.0409 - 3.076 = 8.9649 = 8.96 (2 dp)
QUESTION 3 [3 marks]
£4000 is invested in a fund which earns 11\% compound return per year.
After exactly 1 year, he took £2000 out of this fund.
How much would the fund be worth after 3 years?
Give your answer in pounds, to the nearest penny.
Answer type: Simple text answer
ANSWER: £3006.32
ANSWER: A
WORKING:
Year 1: £4000 \times 1.11 = £4440
Year 1 remaining: £4440 - £2000 = £2440
Year 2: £2440 \times 1.11 = £2708.40
Year 3: £2708.40 \times 1.11 = £3006.32 (nearest penny)
QUESTION 4 [4 marks]
In a rowing team, the weight of 8 women, in kilograms, is:
63.2, \, 60.7, \,57.4, \,66.3, \,62.5, \,65.2, \,69.9, \,58.1
In order to be a more competitive team, the coach has said that each team member should try to increase their overall muscle mass which will result in a 2.5\% gain in overall body weight.
What will be the mean weight of the team if all 8 are successful in precisely meeting this 2.5\% weight gain?
Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 63.75 kg
WORKING:
The combined weight of all 8 members is:
63.2 + 60.7 + 57.4 + 66.3 + 62.5 + 65.2 + 69.9 + 58.1 = 503.3 kg
Combined weight after 2.5\% weight gain:
503.3 \times 1.025 = 515.8825 kg
Mean = 515.8825 \div \, 8 =64.49 kg (2 dp)
QUESTION 5 [5 marks]
140 students from Year 12 and Year 13 are studying in an academy. All of the students study either Biology, Chemistry or Physics.
There are 87 students from Year 13, of which 22 take Chemistry. 21 of the 53 students taking Biology are from Year 12
10 of the 43 students taking Physics are from Year 12

Work out the percentage of students in the academy who study Chemistry.
Give your answer to 1 decimal place.
Answer type: Simple text answer
ANSWER: 31.4 \%
WORKING:

Percentage of students studying chemistry = \dfrac{44}{140} \times 100 = 31.4 \% (1 dp)
QUESTION 6 [3 marks]
Mr Smith pays £4.48 for 400 g of Edam cheese and £2.05 for 175 g of Gouda, and buys 250 g of Gorgonzola. Gorgonzola costs £11.60 per kilogram.
Which type of cheese is better value for money per gram?
Answer type: Multiple choice type 1
A: Edam
B: Gouda
C: Gorgonzola
ANSWER: A
WORKING:
Edam: £4.48 \div 400 = £0.0112 per gram
Gouda: £2.05 \div 175 = £0.0117 per gram
Gorgonzola: £11.60 \div 1000= £0.0116 per gram
Edam is better value.
QUESTION 7 [2 marks]
A biology tutor wishes to bulk purchase some notepads for his students. He wants to buy 25 notepads. There is a 3 for the price of 2 offer on the notepads he wishes to buy.
How many notepads will the tutor have to pay for in order to receive 25?
Answer type: Simple text answer
ANSWER: 17
WORKING:
25\div3=8\dfrac{1}{3}
8\dfrac{1}{3}\times2=16\dfrac{2}{3}
So the tutor will need to pay for 17 in order to receive 25 notepads.
QUESTION 8 [5 marks]
Kieran works at an Admin firm. His current working hours ate listed in the table below.

Kieran is not paid for his break times and he earns a standard rate of £9.42 per hour.
On Wednesdays and Saturdays, he works as a delivery driver, earning 25\% more than his normal rate for his admin job, rounded up to the nearest penny.
The delivery driver company he works for pay their staff 1.5 times their hourly rate for any days worked on the weekend.
How much more does Kieran get paid per week from his delivery driver job than his admin job?
Answer type: Simple text answer
ANSWER: £28.36
WORKING:
Admin job:
Total hours worked = 8+9+6.5 = 23.5 hours
Total hours after breaks = 23.5 - 1.5 = 22 hours
Weekly wage = £9.42 \times 22 = £207.24
Delivery driver job:
Weekday hourly rate = £9.42 \times 1.25 = £11.775 = £11.78 (rounded up to nearest penny)
Hours worked during week = 10.5 hours
Hours worked during week after breaks = 10.5 - 1 = 9.5 hours
Wage for weekdays = £11.78 \times 9.5 = £111.91
Weekend hourly rate = £11.78 \times 1.5 = £17.67
Hours worked during weekend = 7.5
Hours worked during weekend after breaks = 7.5 - 0.5 = 7 hours
Wage for weekend = £17.67 \times 7 = £123.69
Weekly wage = £111.91 + £123.69 = £235.60
Difference in weekly wage = £235.60 - £207.24 = £28.36
QUESTION 9 [2 marks]
Spinner A has numbers 1 to 4 on it.
Spinner B has numbers 1 to 3 on it.
Both spinners are spun and the numbers on each are added together to give a score.
What is the probability that the score will be 3 or 4 ?
Give your answer as a fraction in simplest form.
Answer type: Fraction
ANSWER: \dfrac{5}{12}
WORKING:
Possible combinations that give a score of 3 or 4:
1+2, 2+1, 1+3, 2+2, 3+1
Probability of the score being 3 or 4 =\dfrac{5}{4\times3}=\dfrac{5}{12}
QUESTION 10 [1 mark]
A student records the number of cars each of his classmates family has.
They record this data in a table.

What is the mode number of cars?
Answer type: Simple text answer
ANSWER: 1
WORKING:
The number of cars with the highest frequency is 1 car.
QUESTION 11 [5 marks]
Below is gold ingot in the shape of a trapezoidal prism.
The trapezium’s base sides have lengths 6 cm and 5 cm and its perpendicular height is 4.5 cm.
The length of the prism is 12 cm.

The area of a trapezium = \bigg(\dfrac{a+b}{2} \bigg) h
where a and b are the lengths of the base sides and h is the height of the trapezium.
The density of the gold ingot is 19.32 g/cm^3
The current value of gold is \$ 59.06 per gram.
Ali previously bought this gold ingot for £240000
£1 = \$1.35
How much profit could Ali make by selling his gold ingot?
Give your answer in pounds to the nearest penny.
Answer type: Simple text answer
WORKING: £11028.62
Trapezium area = \bigg( \dfrac{6+5}{2} \bigg) \times 4.5 = 24.75 cm^2
Volume of prism = 24.75 \times 12 = 297 cm^3
\text{Mass} = \text{density} \times \text{volume} = 19.32 \times 297 = 5738.04 g
Value of ingot in (\$) dollars = 59.06 \times 5738.04 = \$338888.6424
Value of ingot in (£) pounds = 338888.6424 \div 1.35 = £251028.624 = £251028.62 (nearest penny)
Profit = £251028.62 - £240000 = £11028.62
QUESTION 12 [3 marks]
The table below shows the number of visitors to a maze attraction in 2019

The median number of visitors in 2018 was 4786
Calculate the percentage increase in the median number of visitors from 2018 to 2019
Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER:
WORKING:
For 2019, order the numbers from smallest to largest
3456, 4254, 4310, 5249, 5882, 5902, 6396
The median is the \dfrac{n+1}{2} = \dfrac{8}{2} = 4th value from the ordered list.
Median = 5249
Difference in medians = 5249 - 4786 = 463
Percentage increase = \dfrac{463}{4786} \times 100 = 9.67 \% (2 dp)
QUESTION 13 [1 mark]
What is the number in the thousandths position in 283.157 ?
Answer type: Simple text answer
ANSWER: 7
QUESTION 14 [5 marks]
Joyce wants to replace the grass in her garden with artificial grass. A diagram of her garden is shown below.

The length of the flower bed is \dfrac{3}{5} the length of the garden.
The width of the flower bed is half the width of the garden.
The radius of the circular pond is 2.2 m.
Use \pi = 3.14
Artificial grass is sold in rolls, measuring 210 cm by 375 cm.
The artificial grass can be cut and joined together.
How many rolls of artificial grass will Joyce need to buy?
Answer type: Simple text answer
ANSWER: 7
WORKING:
Length of garden = \dfrac{6.3}{3} \times 5 = 10.5 m
Width of garden = 3.9 \times 2 = 7.8 m
Area of garden = 10.5 \times 7.8 = 81.9 m^2
Area of flower bed = \dfrac{1}{2} \times 3.9 \times 6.3 = 12.285 m^2
Area of pond = 3.14 \times 2.2^2 = 15.1976 m^2
Area of grass = 81.9 - 12.285 - 15.1976 = 54.4174 m^2
Area of roll of artificial grass = 2.1 \times 3.75 = 7.875 m^2
Rolls needed = 54.4174 \div 7.875 = 6.91 ... = 7 whole rolls
QUESTION 15 [1 mark]
There are adults and children in a cinema.
There are 24 adults.
25\% of the people at the cinema are children.
Work out the total number of people at the cinema.
Answer type: Simple text answer
ANSWER: 32
WORKING:
24 \div 0.75 = 32 people
