06. Prime Factors, HCF, LCM - Cardiff Tutor Company

Question 1

LEVEL 4

Find the HCF and LCM of $66$ and $20$ .

Select the correct answer from the options below:

A: HCF = $1$ , LCM = $600$

B: HCF = $2$ , LCM = $660$

C: HCF = $4$ , LCM = $660$

D: HCF = $2$ , LCM = $600$

CORRECT ANSWER: B: HCF = $2$ , LCM = $660$

WORKED SOLUTION:

First we have to find the prime factorisation of $66$ and of $20$ :

Prime factors of $66$ : $2\times3\times11$

Prime factors of $20$ : $2\times2\times5$

Then we can place each prime factor in the correct circle in the Venn diagram. Any common factors should be placed in the intersection of the two circles.

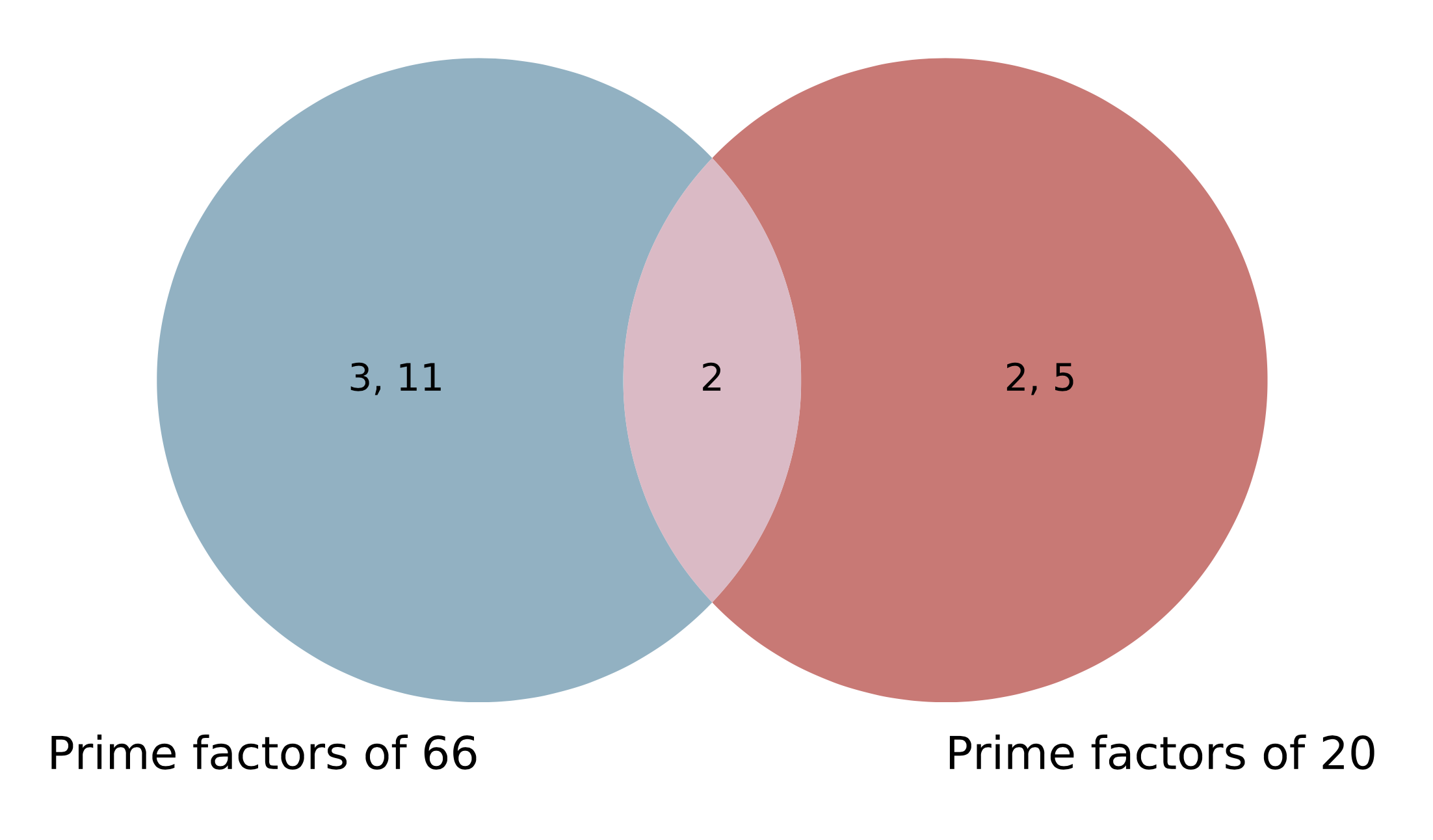
The highest common factor (HCF) is found by multiplying together the numbers in the intersection of the two circles.

HCF = $2$

The lowest common multiple (LCM) is found by multiplying together the numbers from all three sections of the circles.

LCM = $2\times2\times3\times5\times11=660$

Question 2

LEVEL 4

Find the HCF and LCM of $54$ , $48$ and $72$ using a Venn diagram.

Select the correct answer from the options below:

A: HCF = $6$ , LCM = $402$

B: HCF = $8$ , LCM = $432$

C: HCF = $6$ , LCM = $432$

D: HCF = $8$ , LCM = $402$

CORRECT ANSWER: C: HCF = $6$ , LCM = $432$

WORKED SOLUTION:

First we have to find the prime factorisation of $48$ , $54$ and of $72$ :

Prime factors of $48$ : $2\times2\times2\times2\times3$

Prime factors of $54$ : $2\times3\times3\times3$

Prime factors of $72$ : $2\times2\times2\times3\times3$

Then we can place each prime factor in the correct circle in the Venn diagram. Any common factors should be placed in the intersections of the circles.

The highest common factor (HCF) is found by multiplying together the numbers in the intersection of all three of the circles.

HCF = $2\times3=6$

The lowest common multiple (LCM) is found by multiplying together the numbers from all sections of the circles.

LCM = $2\times2\times2\times2\times3\times3\times3=432$

Answer = C: HCF = $6$ , LCM = $432$

Question 3

LEVEL 4

Find the HCF and LCM of $70$ and $175$ .

Select the correct answer from the options below:

A: HCF = $25$ , LCM = $250$

B: HCF = $35$ , LCM = $350$

C: HCF = $25$ , LCM = $350$

D: HCF = $35$ , LCM = $250$

CORRECT ANSWER: B: HCF = $35$ , LCM = $350$

WORKED SOLUTION:

First we have to find the prime factorisation of $70$ and of $175$ :

Prime factors of $70$ : $2\times5\times7$

Prime factors of $175$ : $5\times5\times7$

Then we can place each prime factor in the correct circle in the Venn diagram. Any common factors should be placed in the intersection of the two circles.

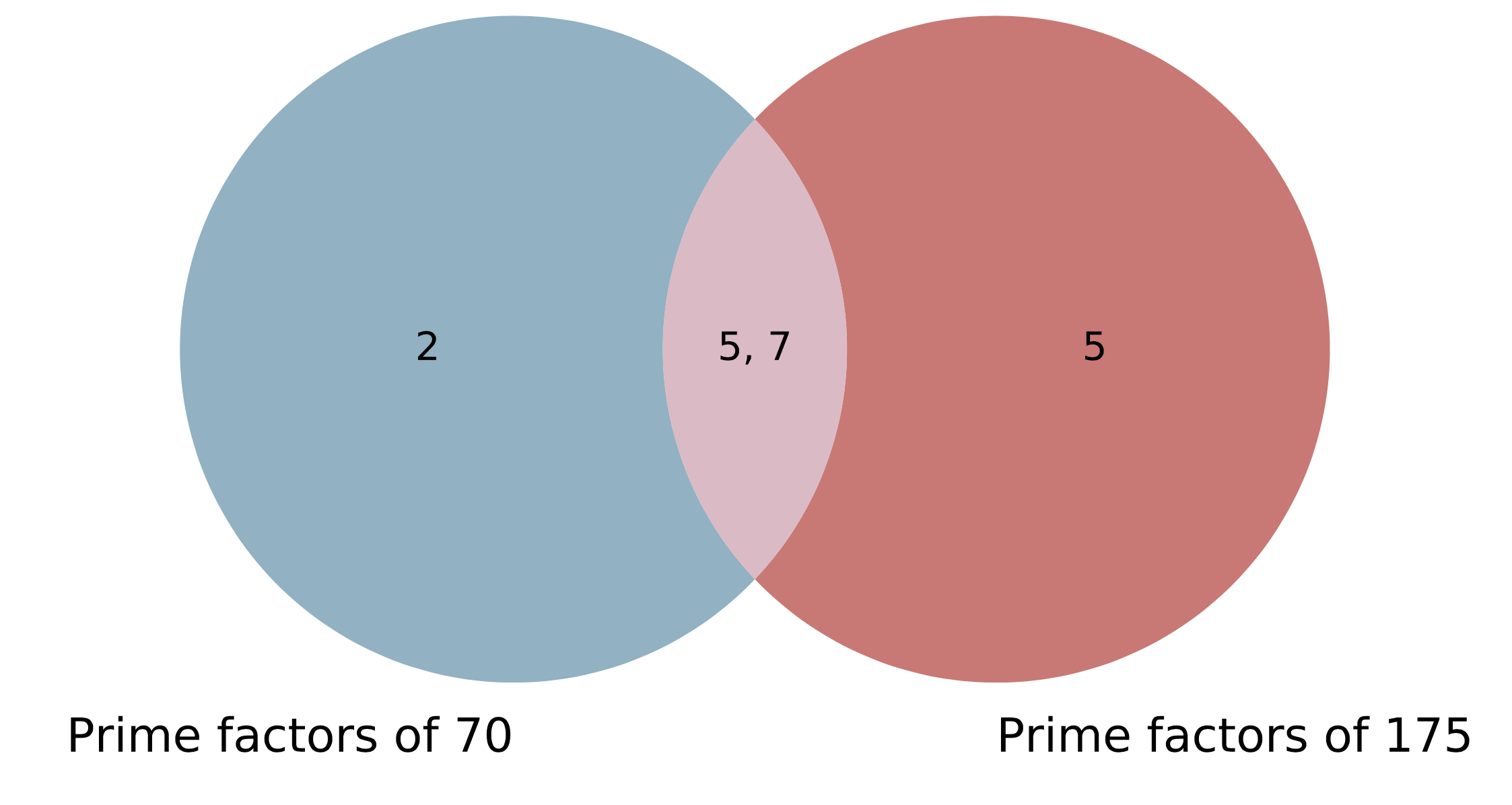
The highest common factor (HCF) is found by multiplying together the numbers in the intersection of the two circles.

HCF = $5\times7=35$

The lowest common multiple (LCM) is found by multiplying together the numbers from all three sections of the circles.

LCM = $2\times5\times5\times7=350$

Question 4

LEVEL 4

Find the HCF and LCM of $44$ , $165$ and $198$ .

Select the correct answer from the options below:

A: HCF = $11$ , LCM = $1180$

B: HCF = $1$ , LCM = $1980$

C: HCF = $11$ , LCM = $1980$

D: HCF = $1$ , LCM = $1180$

CORRECT ANSWER: C: HCF = $11$ , LCM = $1980$

WORKED SOLUTION:

First we have to find the prime factorisation of $44$ , $165$ and of $198$ :

Prime factors of $44$ : $2\times2\times11$

Prime factors of $165$ : $3\times5\times11$

Prime factors of $198$ : $2\times3\times3\times11$

Then we can place each prime factor in the correct circle in the Venn diagram. Any common factors should be placed in the intersections of the circles.

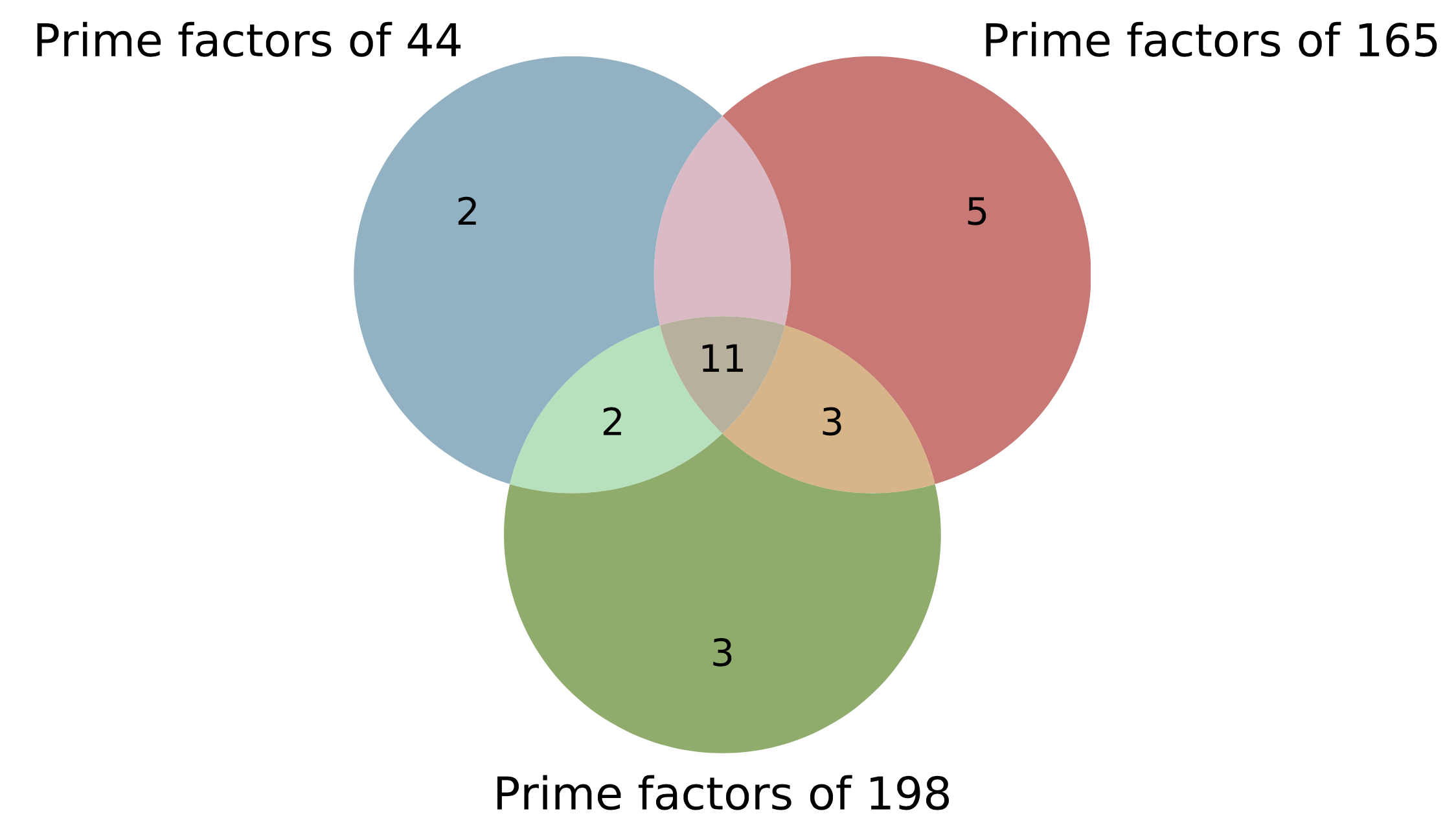
The highest common factor (HCF) is found by multiplying together the numbers in the intersection of all three of the circles.

HCF = $11$

The lowest common multiple (LCM) is found by multiplying together the numbers from all sections of the circles.

LCM = $2\times2\times3\times3\times5\times11=1980$

Answer = C: HCF = $11$ , LCM = $1980$

Question 5

LEVEL 4

Find the HCF and LCM of $32$ , $152$ and $600$ .

Select the correct answer from the options below:

A: HCF = $8$ , LCM = $35600$

B: HCF = $6$ , LCM = $145600$

C: HCF = $8$ , LCM = $45600$

D: HCF = $6$ , LCM = $45600$

CORRECT ANSWER: C: HCF = $8$ , LCM = $45600$

WORKED SOLUTION:

First we have to find the prime factorisation of $32$ , $152$ and of $600$ :

Prime factors of $32$ : $2\times2\times2\times2\times2$

Prime factors of $152$ : $2\times2\times2\times19$

Prime factors of $600$ : $2\times2\times2\times3\times5\times5$

Then we can place each prime factor in the correct circle in the Venn diagram. Any common factors should be placed in the intersections of the circles.

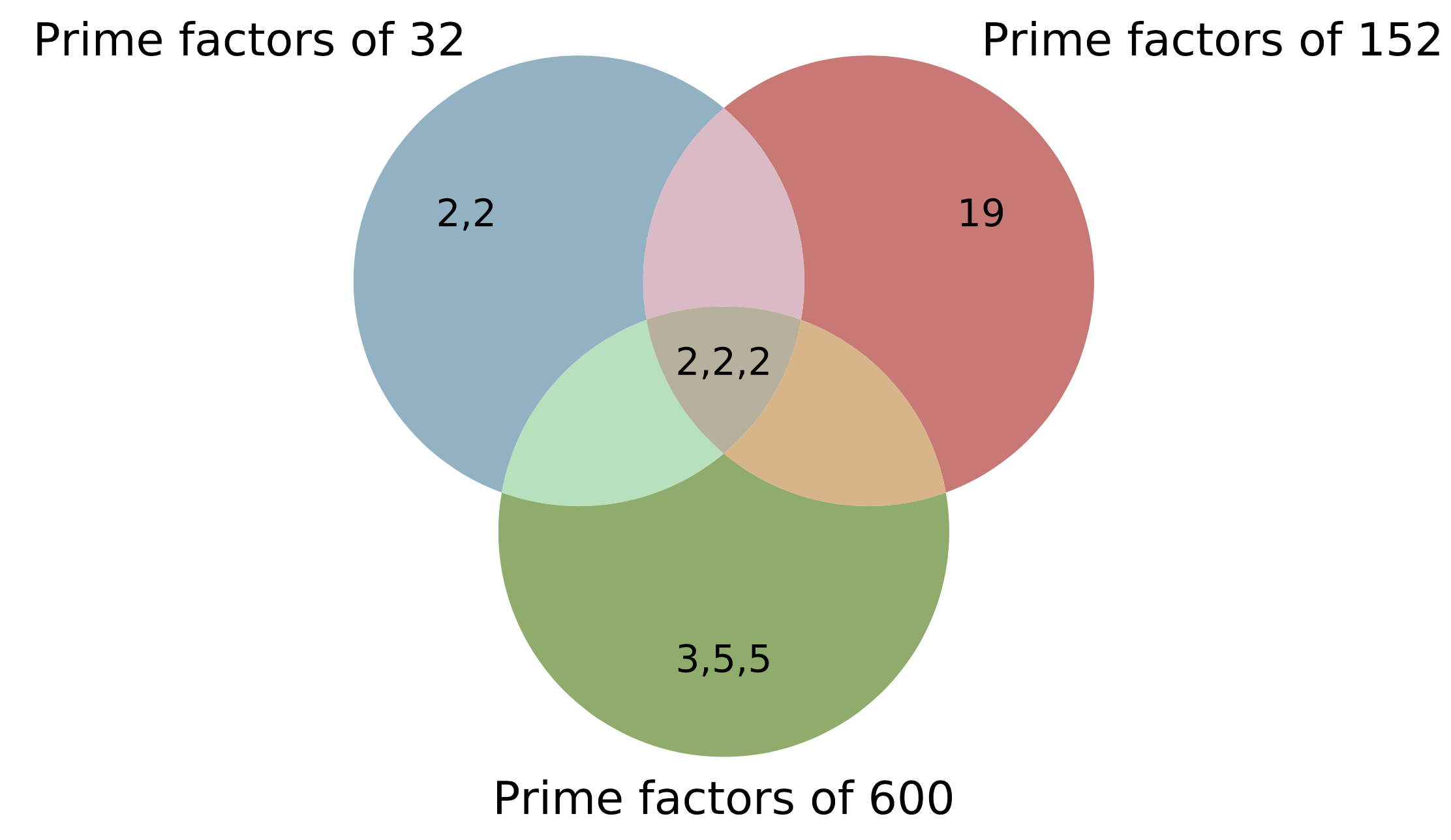
The highest common factor (HCF) is found by multiplying together the numbers in the intersection of all three of the circles.

HCF = $2\times2\times2=8$

The lowest common multiple (LCM) is found by multiplying together the numbers from all sections of the circles.

LCM = $2\times2\times2\times2\times2\times3\times5\times5\times19=45600$

Question 6

LEVEL 4

Find the HCF and LCM of $24$ and $40$ using the buildings method.

Select the correct answer from the list below:

A: HCF= $4$ LCM= $140$

B: HCF= $8$ LCM= $120$

C: HCF= $12$ LCM= $100$

D: HCF= $16$ LCM= $80$

CORRECT ANSWER: B: HCF= $8$ LCM= $120$

WORKED SOLUTION:

First we have to find the prime factorisation of $24$ and of $40$ :

Prime factors of $24$ : $2\times2\times2\times3$

Prime factors of $40$ : $2\times2\times2\times5$

To find the HCF, find any prime factors that are in common between both numbers.

HCF = $2\times2\times2=8$

Next, cross any numbers used so far off from the products.

Prime factors of $24$ : $\cancel{2}\times\cancel{2}\times\cancel{2}\times3$

Prime factors of $40$ : $\cancel{2}\times\cancel{2}\times\cancel{2}\times5$

To find the LCM, multiply the HCF by all the factors that have not been crossed out so far.

LCM = $2 \times 2 \times 2\times3\times5=120$