Question 1
LEVEL 3
Calculate the gradient of the straight line drawn below.
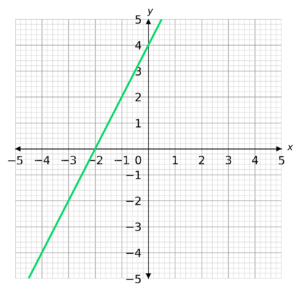
Select the correct answer from the list below:
A: Gradient = 2
B: Gradient = -3
C: Gradient = \dfrac{1}{2}
D: Gradient = -4
CORRECT ANSWER: A: Gradient = 2
WORKED SOLUTION:
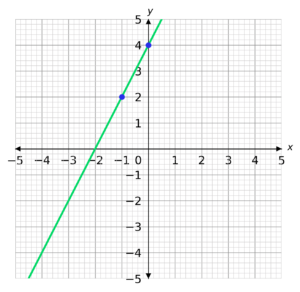 Start by taking two points on the line. It doesn’t matter which two you choose, but it is usually easier to choose two that have whole number co-ordinates.
Start by taking two points on the line. It doesn’t matter which two you choose, but it is usually easier to choose two that have whole number co-ordinates.
We then need to draw a right-angle triangle underneath our graph using the two points we have chosen.
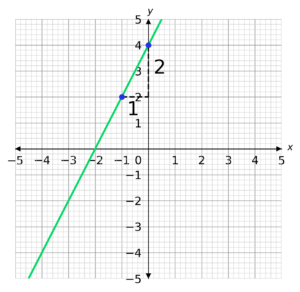
The height of the triangle is the change in y and the length of the base is the change in x.
We now need to divide the change in y by the change in x.
\textrm{Gradient }=\dfrac{2}{1} = 2
Question 2
LEVEL 3
Calculate the gradient of the straight line drawn below.
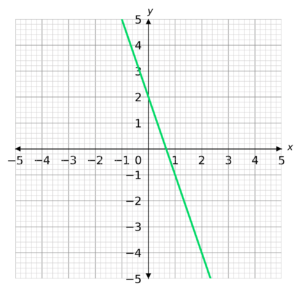
Select the correct answer from the list below:
A: Gradient = 4
B: Gradient = \dfrac{2}{3}
C: Gradient = -3
D: Gradient = -\dfrac{2}{3}
CORRECT ANSWER: C: Gradient = -3
WORKED SOLUTION:
Start by taking two points on the line. It doesn’t matter which two you choose, but it is usually easier to choose two that have whole number coordinates.
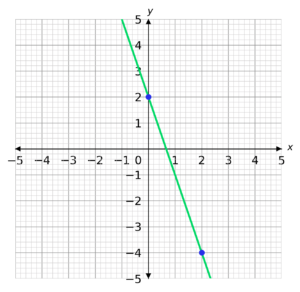
We then need to draw a right-angle triangle underneath our graph using the two points we have chosen.
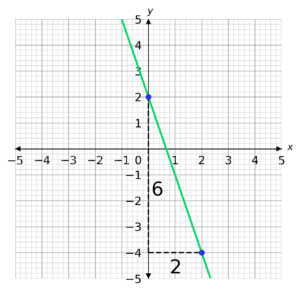
The height of the triangle is the change in y and the length of the base is the change in x.
We now need to divide the change in y by the change in x.
Note, the change in y is going to be negative because it is going down.
\textrm{Gradient }=\dfrac{-6}{2} = -3
Question 3
LEVEL 3
Calculate the gradient of the line drawn below.
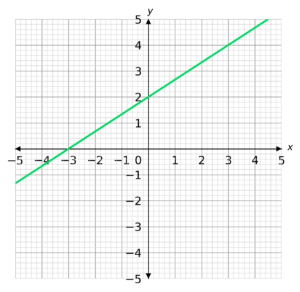
Select the correct answer from the list below:
A: Gradient = \dfrac{2}{3}
B: Gradient = \dfrac{3}{2}
C: Gradient = -\dfrac{2}{3}
D: Gradient = -\dfrac{3}{2}
CORRECT ANSWER: A: Gradient = \dfrac{2}{3}
WORKED SOLUTION:
Start by taking two points on the line. It doesn’t matter which two you choose, but it is usually easier to choose two that have whole number coordinates.
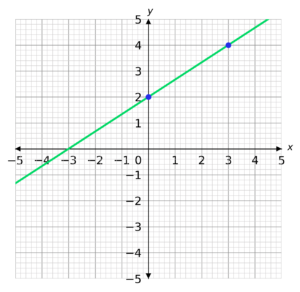
We then need to draw a right-angle triangle underneath our graph using the two points we have chosen.
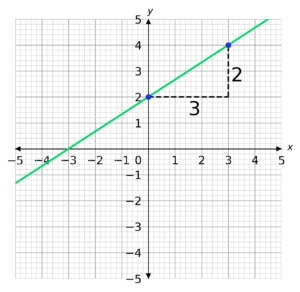
The height of the triangle is the change in y and the length of the base is the change in x.
We now need to divide the change in y by the change in x.
\textrm{Gradient }=\dfrac{2}{3}
Question 4
LEVEL 3
Find the gradient of the line that passes through point A (-1,5) and point B (8, 3).
Select the correct answer from the list below:
A: Gradient = -\dfrac{9}{2}
B: Gradient = -\dfrac{2}{9}
C: Gradient = \dfrac{9}{2}
D: Gradient = \dfrac{2}{9}
CORRECT ANSWER: B: Gradient = -\dfrac{2}{9}
WORKED SOLUTION:
To find the gradient, we’ll subtract the x and y values of one coordinate from the x and y values of the other, and divide the difference in the y values by the difference in the x values:
B-A
\textrm{Gradient }= \dfrac{3-5}{8-(-1)}=\dfrac{-2}{8+1}=\dfrac{-2}{9}=-\dfrac{2}{9}
Or alternatively,
A-B
\textrm{Gradient }= \dfrac{5-3}{-1-8}=\dfrac{2}{-9}=-\dfrac{2}{9}
Question 5
LEVEL 3
Find the gradient of the line that passes through point A (12,13) and point B (7, 7) .
Select the correct answer from the list below:
A: Gradient = -\dfrac{5}{6}
B: Gradient = -\dfrac{6}{5}
C: Gradient = \dfrac{5}{6}
D: Gradient = \dfrac{6}{5}
CORRECT ANSWER: D: Gradient = \dfrac{6}{5}
WORKED SOLUTION:
To find the gradient, we’ll subtract the x and y values of one coordinate from the x and y values of the other, and divide the difference in the y values by the difference in the x values:
B-A
\textrm{Gradient }= \dfrac{7-13}{7-12}=\dfrac{-6}{-5}=\dfrac{6}{5}
A-B
\textrm{Gradient }= \dfrac{13-7}{12-7}=\dfrac{6}{5}
