Question 1
LEVEL 4
Find the midpoint of the following line segment.
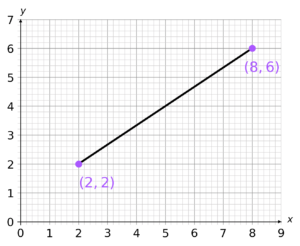
Select the correct answer from the list below:
A: (4,5)
B: (3,2)
C: (3,3)
D: (5,4)
CORRECT ANSWER: D: (5,4)
WORKED SOLUTION:
When finding the midpoint of a line segment, we need to take the average of the endpoints x and y coordinates.
By taking the average of the x coordinates, the x coordinate of the midpoint is:
\frac{8+2}{2}=5By taking the average of the y coordinates, the y coordinate of the midpoint is:
\frac{6+2}{2}=4Therefore, the coordinate of the midpoint is (5,4)
Question 2
LEVEL 4
Find the midpoint of the following line segment.
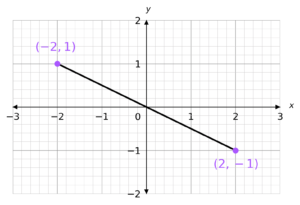
Select the correct answer from the list below:
A: (0,0)
B: (1,1)
C: (-2,-2)
D: (2,1)
CORRECT ANSWER: A: (0,0)
WORKED SOLUTION:
When finding the midpoint of a line segment, we need to take the average of the endpoints’ x and y coordinates.
By taking the average of the x coordinates, the x coordinate of the midpoint is:
\frac{-2+2}{2}=0By taking the average of the y coordinates, the y coordinate of the midpoint is:
\frac{1-1}{2}=0Therefore, the coordinate of the midpoint is (0,0)
Question 3
LEVEL 4
Find the midpoint of a line segment joining the points (-3,4) and (4,6).
Select the correct answer from the list below:
A: \left(\frac{1}{2},5\right)
B: \left(-\frac{1}{2},5\right)
C: \left(5, \frac{1}{2}\right)
D: \left(-\frac{1}{2},10\right)
CORRECT ANSWER: A: \left(\frac{1}{2},5\right)
WORKED SOLUTION:
When finding the midpoint of a line segment, we need to take the average of the endpoints’ x and y coordinates.
By taking the average of the x coordinates, the x coordinate of the midpoint is:
\frac{-3+4}{2}= \frac{1}{2}By taking the average of the y coordinates, the y coordinate of the midpoint is:
\frac{4+6}{2}=5Therefore, the coordinate of the midpoint is \left(\frac{1}{2},5\right)
Question 4
LEVEL 4
Find the midpoint of a line segment joining the points (-10,17) and (-8,23).
Select the correct answer from the list below:
A: (-9,20)
B: (20,-9)
C: (-18,40)
D: (0,0)
CORRECT ANSWER: A: (-9,20)
WORKED SOLUTION:
When finding the midpoint of a line segment, we need to take the average of the endpoints’ x and y coordinates.
By taking the average of the x coordinates, the x coordinate of the midpoint is:
\frac{-10-8}{2}= -9By taking the average of the y coordinates, the y coordinate of the midpoint is:
\frac{17+23}{2}= 20Therefore, the coordinate of the midpoint is (-9,20)
Question 5
LEVEL 4
Find the midpoint of a line segment joining the points (-1,-6) and (-8,-9).
Select the correct answer from the list below:
A: \left(- \frac{9}{2}, - \frac{15}{2}\right)
B: \left( \frac{9}{2}, \frac{15}{2}\right)
C: \left(- 9, - 15\right)
D: \left(- \frac{7}{2}, - \frac{17}{2}\right)
CORRECT ANSWER: A: \left(- \frac{9}{2}, - \frac{15}{2}\right)
WORKED SOLUTION:
When finding the midpoint of a line segment, we need to take the average of the endpoints’ x and y coordinates.
By taking the average of the x coordinates, the x coordinate of the midpoint is:
\frac{-1-8}{2}= - \frac{9}{2}By taking the average of the y coordinates, the y coordinate of the midpoint is:
\frac{-6-9}{2}= - \frac{15}{2}Therefore, the coordinate of the midpoint is \left(- \frac{9}{2}, - \frac{15}{2}\right)
