Question 1
LEVEL 6
The graph below shows the velocity of a motorbike during the first 10 seconds.
Calculate the average acceleration between 2 and 6 seconds.
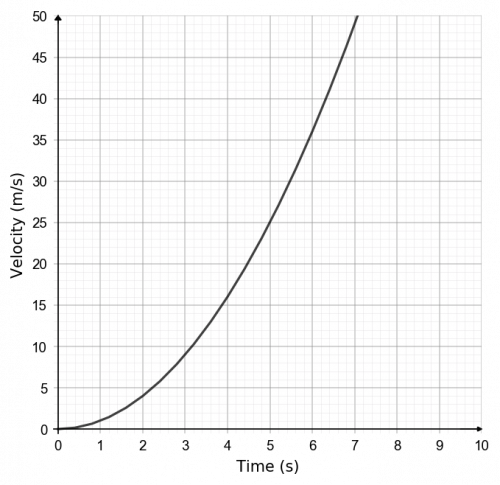
Select the correct answer from the list below:
A: 0.125 m/s^2
B: 4 m/s^2
C: 8 m/s^2
D: 0.25 m/s^2
CORRECT ANSWER: C: 8 m/s^2
WORKED SOLUTION:
To start, we need to draw a line between the two points on the graph at 2 seconds and 6 seconds, as seen on the graph below.

Now we need to find the gradient of the straight line
\text{Gradient} = \dfrac{\text{Change in } y}{\text{Change in } x} = \dfrac{36 - 4}{6 - 2} = \dfrac{32}{4} = 8 m/s^2
Question 2
LEVEL 4
The cost to hire a mountain bike for the week is set at a flat rate plus an amount dependant on the length of the hire. This is represented in the graph below. Calculate the cost per day for hiring a mountain bike.

Select the correct answer from the list below:
A: £7.00
B: £5.25
C: £10.50
D: £17.50
CORRECT ANSWER: C: £10.50
WORKED SOLUTION:
We know that the gradient of the line gives the rate. Here the rate is cost per day, so the cost per day for hiring a mountain bike is
\text{Gradient} = \dfrac{17.5 - 7}{1} = £10.50
Question 3
LEVEL 8
The following graph shows the speed of a car relative to time. Determine the acceleration of the car at 2 seconds.
Select the correct answer from the list below:
A: Between 7.75 and 8.25 m/s^2
B: Between 4.35 and 4.85 m/s^2
C: Between 8.55 and 9.05 m/s^2
D: Between 6.15 and 6.65 m/s^2
CORRECT ANSWER: C: Between 8.55 and 9.05 m/s^2
WORKED SOLUTION:
To start, we need to find the point on our curve where we will be drawing the tangent. We do this by finding the time on the x-axis and then reading up to the curve.
And now we need to draw our tangent, remembering that the tangent only touches the curve and does not cut through.
And now we need to choose two points on the straight line to make our estimate. We may as well use the point where our tangent is, and where it crosses the x-axis gives us a nice y value to use.
And now, we just need to find the gradient of this tangent,
\text{Gradient }=\dfrac{\text{Change in }y}{\text{Change in }x}=\dfrac{8-0}{2-1}=\dfrac{8}{1}=8 m/s^2
Question 4
LEVEL 8
The graph below shows the amount of water left in a jug as it is poured out over time. By choosing two points on the curve, find the rate at which the water is being poured out at 7 seconds.
Select the correct answer from the list below:
A: 65 to 75 ml/s
B: -85 to -75 ml/s
C: 75 to 85 ml/s
D: -75 to - 65 ml/s
CORRECT ANSWER: A: 65 to 75 ml/s
WORKED SOLUTION:
To start, we need to select two points on the curve to create a chord; it is usually good to select the point you are finding the gradient at as one of the two. It can be difficult to choose perfect points or see clearly what the x and y might be, so these will likely be estimates.
And now we need to connect these points with a straight line to create the chord.
And now, we just need to find the gradient of this chord,
\text{Gradient }=\dfrac{\text{Change in }y}{\text{Change in }x}=\dfrac{310-380}{8-7}=\dfrac{-70}{1}=-70 ml/s
Question 5
LEVEL 8
£2500 is put into a fund for a baby when she was born. The graph below shows how the fund has increased over the first 8 years. Find the rate of change at 6 years.
Select the correct answer from the list below:
A: £415 to £515 a year
B: £75 to £175 a year
C: £310 to £410 a year
D: £190 to £290 a year
CORRECT ANSWER: D: £190 to £290 a year
WORKED SOLUTION:
To start, we need to find the point on our curve where we will be drawing the tangent. We do this by finding the time on the x-axis and then reading up to the curve.
And now we need to draw our tangent, remembering that the tangent only touches the curve and does not cut through.
And now we need to choose two points on the straight line to make our estimate. We may as well use the point where our tangent is and the point (8,3600), simply because it is easy to see the x and y values. It is worth noting that these will be estimates.
And now, we just need to find the gradient of this tangent,
\text{Gradient }=\dfrac{\text{Change in }y}{\text{Change in }x}=\dfrac{3600-3100}{8-6}=\dfrac{500}{2}= £250 per year











