02. y=mx+c v2

Question 1

LEVEL 4

Find the value of m  for the straight line shown below.

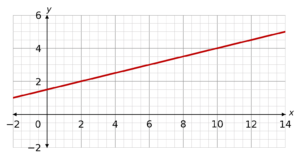
Select the correct answer from the list below:

A: m=-4

B: m=4

C: m=-1/4

D: m=1/4

CORRECT ANSWER: D: m=1/4

WORKED SOLUTION:

Start by taking two points on the line. It doesn’t matter which two you choose, but it is usually easier to choose two that have whole number coordinates.

To find the gradient, we’ll subtract the x and y values of one coordinate from the x and y values of the other, and divide the difference in the y values by the difference in the x values:

Here we will use the points  A (2,2) and  B (10,4).

B-A

\textrm{Gradient }= \dfrac{4-2}{10-2}=\dfrac{2}{8}=\dfrac{1}{4}

Or alternatively,

A-B

\textrm{Gradient }= \dfrac{2-4}{2-10}=\dfrac{-2}{-8}=\dfrac{1}{4}

Question 2

LEVEL 4

Find the equation of the straight line below

Select the correct answer from the list below:

A: y=\dfrac{1}{4}x+1.5

B: y=\dfrac{1}{2}x+0.5

C: y=-\dfrac{1}{4}x+1.8

D: y=-\dfrac{1}{2}x+1.5

CORRECT ANSWER:   A: y=\dfrac{1}{4}x+1.5

WORKED SOLUTION:

Start by taking two points on the line. It doesn’t matter which two you choose, but it is usually easier to choose two that have whole number coordinates.

To find the gradient, we’ll subtract the x and y values of one coordinate from the x and y values of the other, and divide the difference in the y values by the difference in the x values:

Here we will use the points  A (2,2) and  B (10,4).

B-A

\textrm{Gradient }= \dfrac{4-2}{10-2}=\dfrac{2}{8}=\dfrac{1}{4}

Now to find the y-intercept.

This can be achieved by considering the graph above and reading the value at the point at which the line crosses the y-axis.

Or it can be achieved mathematically be substituting a coordinate the line passes through into the equation,

y = \dfrac{1}{4}x+c

Here we will use the point  A (2,2) to substitute in to the equation such that,

2 = \dfrac{1}{4}\times2+c

c=2-\dfrac{2}{4}=1.5

So the equation of the line is,

y = \dfrac{1}{4}x+1.5

Question 3

LEVEL 4

Find the equation of the line which has a gradient of 5 and passes through the co-ordinate (2, 5).

Select the correct answer from the list below:

A: y=\dfrac{1}{5}x-5

B: y=5x+5

C: y=5x-5

D: y=\dfrac{1}{5}x+5

CORRECT ANSWER:  C: y=5x-5

WORKED SOLUTION:

Start by taking two points on the line. It doesn’t matter which two you choose, but it is usually easier to choose two that have whole number coordinates.

To find the gradient, we’ll subtract the x and y values of one coordinate from the x and y values of the other, and divide the difference in the y values by the difference in the x values:

Here we will use the points  A (0,-5) and  B (2,5).

B-A

\textrm{Gradient }= \dfrac{5-(-5)}{2-0}=\dfrac{10}{2}=5

Now to find the y-intercept.

This can be achieved by considering the graph above and reading the value at the point at which the line crosses the y-axis.

Or it can be achieved mathematically be substituting a coordinate the line passes through into the equation,

c=-5

So the equation of the line is,

y = 5x-5

Question 4

LEVEL 4

Find the equation of the line which has a gradient of -\dfrac{1}{5} and passes through the co-ordinate (4, 1.2).

Select the correct answer from the list below:

A: y=-\dfrac{1}{5} x+2

B: y=-\dfrac{1}{5} x+3

C: y=-\dfrac{1}{5} x+4

D: y=-\dfrac{1}{5} x+5

CORRECT ANSWER:  A: y=-\dfrac{1}{5} x+2

WORKED SOLUTION:

Start by taking two points on the line. It doesn’t matter which two you choose, but it is usually easier to choose two that have whole number coordinates.

To find the gradient, we’ll subtract the x and y values of one coordinate from the x and y values of the other, and divide the difference in the y values by the difference in the x values:

Here we will use the points  A (0,2) and  B (4,1.2).

B-A

\textrm{Gradient }= \dfrac{1.2-2}{4-0}=\dfrac{-0.8}{4}=-\dfrac{1}{5}

Now to find the y-intercept.

This can be achieved by considering the graph above and reading the value at the point at which the line crosses the y-axis.

Or it can be achieved mathematically be substituting a coordinate the line passes through into the equation,

c=2

So the equation of the line is,

y = -\dfrac{1}{5}x+2

Question 5

LEVEL 4

Given that co-ordinates (5, 1.5) and (7, 4.5) lie on the same line, give the equation of the line.

Select the correct answer from the list below:

A: y=\dfrac{7}{5} x-6

B: y=\dfrac{4}{2} x-6

C: y=\dfrac{3}{2} x-6

D: y=\dfrac{3}{2} x-4

CORRECT ANSWER: C: y=\dfrac{3}{2}x -6

WORKED SOLUTION:

Start by taking two points on the line. It doesn’t matter which two you choose, but it is usually easier to choose two that have whole number coordinates.

Plot the co-ordinates (5, 1.5) and (7, 4.5)

Draw a line between them that continues on after each point.

Draw a dotted line from the upper co-ordinate down to the y-number value of the bottom co-ordinate.

Draw a dotted line from that point to your bottom co-ordinate.

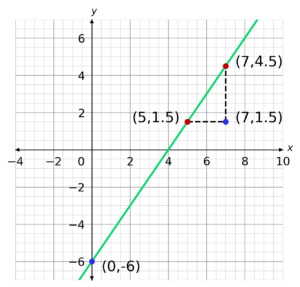
Either count the difference in vertical squares divided by the difference of horizontal squares from the upper coordinate to the lower coordinate, or use the formula

m=\dfrac{y_1-y_2}{x_1-x_2}

m = \dfrac{4.5 - 1.5}{7 - 5} = \dfrac{3}{2}

Using the formula y = mx + c

Substitute the coordinates of a point the line passes through e.g. (4,0)

0 = \dfrac{3}{2} \times 4 + c

c = -6

Hence equation of the line is:

y = \dfrac{3}{2}x - 6

Question 6

LEVEL 4

Given that co-ordinates (-5, -2) and (5,-6) lie on the same line, find the y-intercept.

Select the correct answer from the list below:

A: y-intercept = 4

B: y-intercept = -4

C: y-intercept = 8

D: y-intercept = -8

CORRECT ANSWER:   B: y-intercept = -4

WORKED SOLUTION:

Start by taking two points on the line. It doesn’t matter which two you choose, but it is usually easier to choose two that have whole number coordinates.

To find the gradient, we’ll subtract the x and y values of one coordinate from the x and y values of the other, and divide the difference in the y values by the difference in the x values:

Here the coordinates are (-5, -2) and (5,-6)

\textrm{Gradient }= \dfrac{-6-(-2)}{5-(-5)}=\dfrac{-4}{10}=-\dfrac{2}{5}

Substitute y, m and x into the formula y=mx+c to give,

-2=-\dfrac{2}{5}\times-5+c

-2=2+c

c=-4

Hence the y-intercept = -4

Question 7

LEVEL 4

Find the gradient and the y-intercept of the line x + 3y = 15

Select the correct answer from the list below:

A: y-intercept = 5, gradient = \dfrac{1}{3}

B: y-intercept = 15, gradient = -1

C: y-intercept = 5, gradient = - \dfrac{1}{3}

D: y-intercept = 15, gradient = 1

CORRECT ANSWER:  C: y-intercept = 5, gradient = - \dfrac{1}{3}

WORKED SOLUTION:

We need to rearrange x + 3y = 15 to make y the subject. So, subtracting x from both sides, we get

3y = -x + 15

Then, dividing both sides by 3, we get

y = - \dfrac{1}{3} x + 5

Therefore the y-intercept is 5 and the gradient is - \dfrac{1}{3}.