12.5. Invariant Points - Cardiff Tutor Company

Question 1

LEVEL 4

A square $ABCD$ is shown on the grid below:

$ABCD$ is rotated around point $(1,1)$

Select the invariant point from the list below:

A: $A$

B: $B$

C: $C$

D: $D$

CORRECT ANSWER: D: $D$

WORKED SOLUTION:

If the shape is rotated about $(1,1)$ , for example by $90\degree$ the point $D$ is invariant.

Question 2

LEVEL 4

A square $ABCD$ is shown on the grid below:

$ABCD$ is reflected in line $y=1$

Select the invariant points from the list below:

A: $A$ and $D$

B: $B$ and $C$

C: $C$ and $D$

D: $D$ and $B$

CORRECT ANSWER: C: $C$ and $D$

WORKED SOLUTION:

If the shape is reflected in $y=1$ then the points $C$ and $D$ are invariant.

Question 3

LEVEL 4

A square $ABCD$ is shown on the grid below:

$ABCD$ is reflected in line $x=1$

Select the invariant points from the list below:

A: $A$ and $D$

B: $B$ and $C$

C: $C$ and $D$

D: $D$ and $B$

CORRECT ANSWER: A: $A$ and $D$

WORKED SOLUTION:

If the shape is reflected in $x=1$ then the points $A$ and $D$ are invariant.

Question 4

LEVEL 4

A triangle $ABC$ is shown on the grid below:

$ABCD$ is reflected in the line $y=2$

Select the invariant points from the list below:

A: $A$ and $B$

B: $C$ and $B$

C: $A$ and $C$

D: $B$ and $A$

CORRECT ANSWER: B: $C$ and $B$

WORKED SOLUTION:

If the shape is reflected in $y=2$ then the points $B$ and $C$ are invariant.

Question 5

LEVEL 4

A triangle $ABC$ is shown on the grid below:

$ABCD$ is reflected in the line $x=1$

Select the invariant points from the list below:

A: $A$ and $B$

B: $A$ and $C$

C: $C$ and $B$

D: $B$ and $A$

CORRECT ANSWER: B: $A$ and $C$

WORKED SOLUTION:

If the shape is reflected in $x=1$ then the points $A$ and $C$ are invariant.

Question 6

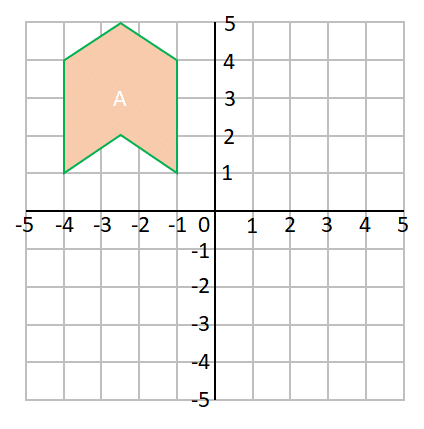
Reflect the shape A in the line $y=1$ , marking any invariant points.

Select the correct answer from the list below:

CORRECT ANSWER: B

WORKED SOLUTION:

To start, we need to draw our line of reflection, $y=1$ . This will be a horizontal line thorough $y=1$ .

We now need to measure the distance of points from the line. Luckily, two of these are on the line so won’t move.

All other points will move, one of which will look like this

If we repeat this with the other points and connect the dots we will get a shape that looks like this:

And now we need to mark the invariant points, which are the points that started by touching the line of reflection