Question 1
Calculate the area of the circle segment below
Give your answer to 2 decimal places.

Select the correct answer from the list below:
A: 55. 86 m^2
B: 72.91 m^2
C: 61.09 m^2
D: 81.24 m^2
CORRECT ANSWER: C: 61.1 m^2
WORKED SOLUTION:
To work out the area of the sector when can consider the sector to be a fraction of a complete circle of radius 10 m.
Area of a complete circle with a radius, r= 10m:
Area =\pi\times10^2=100\pi m^2
Hence the area of the sector is a fraction of this total area which we can calculate by considering the angle as a fraction of 360\degree ,
Area of sector =\dfrac{70}{360}\times\pi\times10^2
Area of sector =\dfrac{7}{36}\times100\pi =\dfrac{175}{9}\pi=61.1 m^2
Question 2
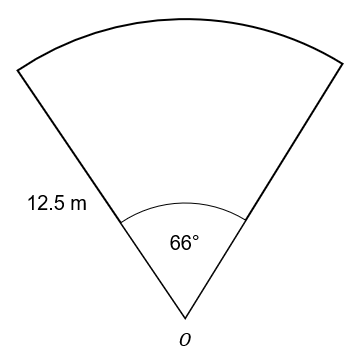
Calculate the area of the circle segment below
Give your answer to 2 decimal places.
Select the correct answer from the list below:
A: 89.99 m^2
B: 86.29 m^2
C: 79.79 m^2
D: 73.59 m^2
CORRECT ANSWER: A: 89.99 m^2
WORKED SOLUTION:
To work out the area of the sector when can consider the sector to be a fraction of a complete circle of radius 12.5 m.
Area of a complete circle with a radius, r= 12.5m:
Area =\pi\times12.5^2=156.25\pi m^2
Hence the area of the sector is a fraction of this total area which we can calculate by considering the angle as a fraction of 360\degree ,
Area of sector =\dfrac{66}{360}\times\pi\times12.5^2
Area of sector =\dfrac{11}{60}\times156.25\pi =\dfrac{1375}{48}\pi=89.99 m^2
Question 3
Calculate the arc length of the circle segment below.
Give your answer to 2 decimal places.

Select the correct answer from the list below:
A: 12.22m
B: 16.83m
C: 13.49m
D: 14.40m
CORRECT ANSWER: D: 14.40m
WORKED SOLUTION:
To find the arc length of a sector we can first calculate the length of the entire circumference of a circle with the same radius, then multiple that value by the fraction of the angle over 360\degree .
Circumference of total circle = 2\times \pi \times r = 25\pi
As we now have the circumference of a similar complete circle we can find the circumference of the sector,
Circumference of sector = \dfrac{66}{360}\times 25\pi = 14.40 m
Question 4
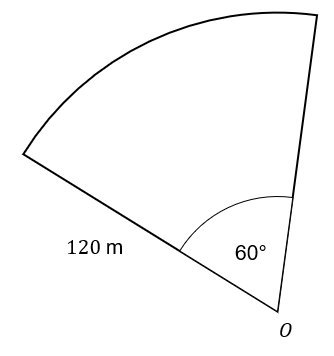
Calculate the perimeter of the circle segment below
Give your answer to 2 decimal places.
Select the correct answer from the list below:
A: 388.42mm
B: 365.66mm
C: 377.31mm
D: 344.68mm
CORRECT ANSWER: B: 365.66mm
WORKED SOLUTION:
To find the arc length of a sector we can first calculate the length of the entire circumference of a circle with the same radius, then multiple that value by the fraction of the angle over 360\degree .
arc length = \dfrac{60}{360}\times2\times \pi \times 120 = 40\pimm
Now a sector consits of an arc and two radii so the perimeter is the sum of the length of those radii and the arc length so,
perimeter = 40\pi +120 +120 = 365.66mm
Question 5
Calculate the perimeter of the circle segment below
Give your answer to 2 decimal places.

Select the correct answer from the list below:
A: 14.72m
B: 19.54m
C: 12.90m
D: 15.24m
CORRECT ANSWER: D: 15.24m
WORKED SOLUTION:
To find the arc length of a sector we can first calculate the length of the entire circumference of a circle with the same radius, then multiple that value by the fraction of the angle over 360\degree .
arc length = \dfrac{60}{360}\times2\times \pi \times 5 = \dfrac{5}{3}\pim
Now a sector consits of an arc and two radii so the perimeter is the sum of the length of those radii and the arc length so,
perimeter = \dfrac{5}{3}\pi+5+5 = 15.24m
