Question 1
LEVEL 6
Given that shapes A and B are similar, and that shape B is a scale factor of 3 times bigger than A, work out the area of B.
Select the correct answer from the list below:
A: \dfrac{7}{3} cm^2
B: 21 cm^2
C: 63 cm^2
D: 147 cm^2
CORRECT ANSWER: C: 63 cm^2
WORKED SOLUTION:
To find the area of a second shape based on the scale factor, we have to multiply the original area by the square of the scale factor.
\text{Area of B}=7\times3^2=7\times9=63 cm^2
Question 2
LEVEL 6
The diagram shows two similar shapes, A and B.
Shape A has an area of 15 m^2 and shape B has an area of 60 m^2. Shape A has a side length of 3 cm.
Find the value of x from shape B.

Select the correct answer from the list below:
A: 6 cm
B: 4 cm
C: 9 cm
D: 2 cm
CORRECT ANSWER: A: 6 cm
WORKED SOLUTION:
The scale factor between the areas is 60 \div 15 = 4
Therefore the scale factor between the side lengths is \sqrt{4} = 2
Therefore, x = 3 \times 2 = 6 cm
Question 3
LEVEL 6
The diagram shows two similar solids, shape A and shape B.
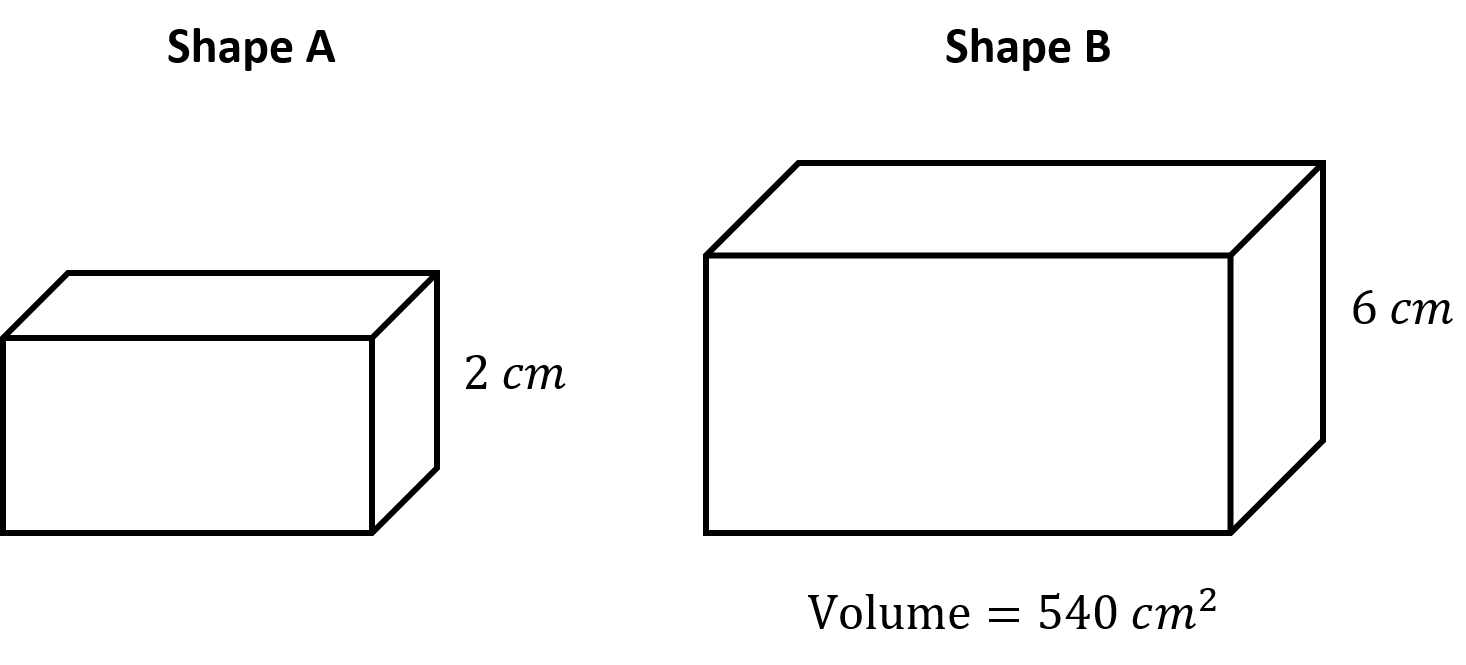
Calculate the volume of shape A.
Select the correct answer from the list below:
A: 20 cm^3
B: 60 cm^3
C: 270 cm^3
D: 180 cm^3
CORRECT ANSWER: A: 20 cm^3
WORKED SOLUTION:
The scale factor between side lengths is 6 \div 2 = 3
Therefore the scale factor between volumes is 3^3 = 27
To find the volume of shape A we need to divide the volume of shape B by this scale factor
We get, Volume of Shape A = 540 \div 27 = 20 cm ^3
Question 4
LEVEL 6
Two spheres are similar shapes. Sphere A has a radius of 4 cm and Sphere B has a radius of 8 cm.
Calculate the ratio of the volumes between the two spheres.
Select the correct answer from the list below:
A: 1:8
B: 1:4
C: 1:2
D: 1:16
CORRECT ANSWER: A: 1:8
WORKED SOLUTION:
The scale factor between lengths is 8 \div 4 = 2
Therefore the scale factor between volumes is 2^3= 8
Therefore the ratio between volumes is 1:8
Question 5
LEVEL 6
Shape A and Shape B are similar shapes. Shape A has an area of 25 cm^2.
Calculate the area of Shape B.

Select the correct answer from the list below:
A: 156.25 cm^2
B: 62.5 cm^2
C: 125 cm^2
D: 60 cm^2
CORRECT ANSWER: A: 156.25 cm^2
WORKED SOLUTION:
The scale factor between lengths is 17.5 \div 7 = 2.5
Therefore the scale factor between areas is 2.5^2 = 6.25
To find the area of shape B we need multiply the area of shape A by this scale factor
We get, 25 \times 6.25 = 156.25 cm^2

